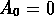We would like to outline our research plan by discussing some recent controversies which appeared in the study of hot gluon plasma. The research aimed at the solution of these problems, however, will also be extended to the study of other physical systems.
The chaotic dynamics of long wavelength, classical, nonabelian
Yang-Mills fields can be best demonstrated by inspecting the
Hamiltonian of the gluonic zero modes in the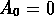 
gauge.
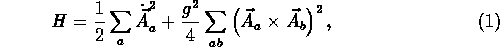
where all spatial derivatives has been neglected.
Assuming that only two vector potential field components,
say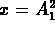 
and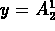 
(i.e. a pair dual in color and
spatial polarization), are nonzero the Hamiltonian reduces to
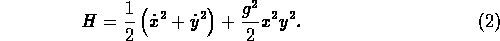
This describes a conservative motion of a pointlike particle
in two dimensions. The potential energy,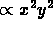 
,
defines a hyperbola as the boundary of the motion with a given
(constant) energy. This boundary is the set of turning points
of possible classical trajectories.
While near to one of the axes (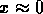
or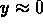 
)
the motion is quasi -- regular, in the center of the classically
allowed configuration space it is irregular.
The hyperbolic boundary can be viewed as a reflecting wall,
which defocuses all nearby classical trajectories due to its
overall negative local curvature [3,4,5].
Medium effects at finite temperature, like Debye screening in a plasma, give rise to a mass of these long wavelength field components [31,32]. This modifies the Hamiltonian
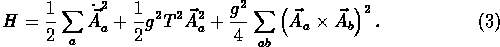
The inertia due to the dynamically generated mass, m = gT, is proportional to the temperature, T, of the medium in thermal equilibrium. This system shows chaotic dynamical behavior only if the control parameter,
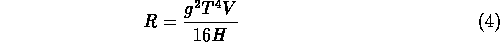
is below the critical value of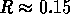 
[5].
For the free gluon system at high temperature the energy
density is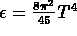 
according to the
Stefan -- Boltzmann law for radiation in thermal equilibrium.
Assuming that the same amount of energy,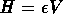 
, is concentrated in
the chaotically behaving infrared modes x and y we would expect
chaos to occur only at couplings weaker than
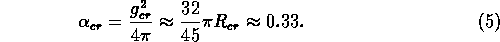
This value is characteristic for temperatures in the range of the
color deconfinement (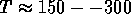
MeV). Sufficient
energy for such temperatures can be achieved in heavy ion collisions
at CERN SPS and RHIC.
This expectation can be contrasted to the hot perturbative QCD
approach, where the mass term of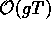 
is obtained in
a lower order calculation than effects related to chaotic
dynamics, like the gluon damping rate of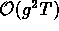 
.
Here, besides an expansion in the coupling strength g, a
hierarchy of hard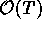 
, soft 
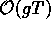and eventually
supersoft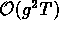 
momenta is used.
In the effective Hamiltonian for soft plasmons, the long wavelength
low energy field components, the self - energy term
(
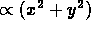) is considered to be dominant.
In this approach no chaotic behavior is apparent
for small amplitudes x and y [33].
In order to achieve a connection between these competing views of high energy gluon dynamics and also to develop dynamical descriptions realistic in non - equilibrium situations, we propose to investigate the relative strength of classical and quantum effects on the chaotic or non -- chaotic nature of such extended field systems.