Multipole expansion classes and methods. More...
Classes | |
| class | Y |
| Class for spherical harmonic functions. More... | |
| class | Yre |
| Class for real spherical harmonic functions. More... | |
| class | Coeff< GReal_t > |
| Class for real spherical harmonic (Yre) expansion coefficients. More... | |
| class | Coeff< GComplex_t > |
| Class for complex spherical harmonic (Y) expansion coefficients. More... | |
| class | ScalarFieldMP< GReal_t > |
| Class for real scalar fields on sphere. More... | |
| class | ScalarFieldMP< GComplex_t > |
| Class for complex scalar fields on sphere. More... | |
Functions | |
| Coeff< GReal_t > | operator* (const GReal_t, const Yre &) |
| Tensor product of a number and an Yre. | |
| Coeff< GReal_t > | operator* (const Yre &, const GReal_t) |
| Coeff< GReal_t > | operator/ (const Yre &, const GReal_t) |
| Tensor quotient of a number and an Yre. | |
| Coeff< GReal_t > | operator* (const GReal_t, const Coeff< GReal_t > &) |
| Multiply a coefficient by a number. | |
| Coeff< GReal_t > | operator* (const Coeff< GReal_t > &, const GReal_t) |
| Coeff< GReal_t > | operator/ (const Coeff< GReal_t > &, const GReal_t) |
| Divide a coefficient by a number. | |
| Coeff< GReal_t > | operator- (const Yre &) |
| Negative of a coefficient. | |
| Coeff< GReal_t > | operator- (const Coeff< GReal_t > &) |
| Coeff< GComplex_t > | operator* (const GReal_t, const Y &) |
| Tensor product of a number and an Y. | |
| Coeff< GComplex_t > | operator* (const Y &, const GReal_t) |
| Coeff< GComplex_t > | operator* (const GComplex_t &, const Y &) |
| Coeff< GComplex_t > | operator* (const Y &, const GComplex_t &) |
| Coeff< GComplex_t > | operator/ (const Y &, const GReal_t) |
| Tensor quotient of a number and an Y. | |
| Coeff< GComplex_t > | operator/ (const Y &, const GComplex_t &) |
| Coeff< GComplex_t > | operator* (const GReal_t, const Coeff< GComplex_t > &) |
| Multiply a coefficient by a number. | |
| Coeff< GComplex_t > | operator* (const Coeff< GComplex_t > &, const GReal_t) |
| Coeff< GComplex_t > | operator* (const GComplex_t &, const Coeff< GComplex_t > &) |
| Coeff< GComplex_t > | operator* (const Coeff< GComplex_t > &, const GComplex_t &) |
| Coeff< GComplex_t > | operator/ (const Coeff< GComplex_t > &, const GReal_t) |
| Divide a coefficient by a number. | |
| Coeff< GComplex_t > | operator/ (const Coeff< GComplex_t > &, const GComplex_t &) |
| Coeff< GComplex_t > | operator- (const Y &) |
| Negative of a coefficient. | |
| Coeff< GComplex_t > | operator- (const Coeff< GComplex_t > &) |
| Coeff< GComplex_t > | conj (const Y &) |
| Complex conjugate a coefficient. | |
| Coeff< GComplex_t > | conj (const Coeff< GComplex_t > &) |
| GReal_t | YYY_coupling (const int l1, const int l2, const int l3, const int m1, const int m2, const int m3) |
The  spherical harmonic function Gaunt coefficient calculator routine. spherical harmonic function Gaunt coefficient calculator routine. | |
| bool | YYY_coupling_zeros (const int l1, const int l2, const int l3, const int m1, const int m2, const int m3) |
| Returns true if the Gaunt coefficient of given index is known to be zero. | |
| unsigned int | YYY_coupling_size () |
| Show table size currently used in YYY_coupling. | |
| GReal_t | YreYreYre_coupling (const int l1, const int l2, const int l3, const int m1, const int m2, const int m3) |
| The same coupling for Yre basis. | |
| GComplex_t | YYreY_coupling (const int l1, const int l2, const int l3, const int m1, const int m2, const int m3) |
| Similar coupling for Y and Yre basis. | |
| GReal_t | intYl1ExpMIPhi (const int l) |
Calculation of 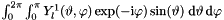 . . | |
| GReal_t | ExpPmIPhiYY_coupling (const int l1, const int m1, const int l2, const int sign) |
The overlap integrals 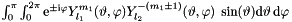 . . | |
| unsigned int | ExpPmIPhiYY_coupling_size () |
| Show table size currently used in ExpPmIPhiYY_coupling. | |
| GReal_t | intYl0 (const int l, const GReal_t theta) |
Calculation of ![$\int_{[0,\theta]\times[0,2\pi]} Y_{l}^{0} \;\mathrm{d}\lambda_{S^2}$](form_55.png) . . | |
| GReal_t | intBarYl1mYl2m (const int l1, const int l2, const int m, const GReal_t theta, tvector< tvector< tvector< GReal_t > > > *coeffstorage) |
Calculation of ![$\int_{[0,\theta]\times[0,2\pi]} \bar{Y}_{l_1}^{m} Y_{l_2}^{m} \;\mathrm{d}\lambda_{S^2}$](form_58.png) . . | |
| GReal_t | SobolevConstantS2 (const int m) |
The minimal Sobolev constant in the inequality over the sphere: 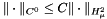 . . | |
| GReal_t | tailSumS2 (const int mup, const int mu, const int L) |
The sum 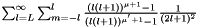 . . | |
| ScalarFieldMP< GReal_t > | operator+ (const ScalarFieldMP< GReal_t > &, const ScalarFieldMP< GReal_t > &) |
| ScalarFieldMP<GReal_t> algebraic operators. | |
| ScalarFieldMP< GReal_t > | operator- (const ScalarFieldMP< GReal_t > &, const ScalarFieldMP< GReal_t > &) |
| ScalarFieldMP< GReal_t > | operator- (const ScalarFieldMP< GReal_t > &) |
| ScalarFieldMP< GReal_t > | operator* (const ScalarFieldMP< GReal_t > &, const GReal_t) |
| ScalarFieldMP< GReal_t > | operator* (const GReal_t, const ScalarFieldMP< GReal_t > &) |
| ScalarFieldMP< GReal_t > | operator* (const ScalarFieldMP< GReal_t > &, const ScalarFieldMP< GReal_t > &) |
| ScalarFieldMP< GReal_t > | operator/ (const ScalarFieldMP< GReal_t > &, const GReal_t) |
| GReal_t | L2S2 (const ScalarFieldMP< GReal_t > &, const ScalarFieldMP< GReal_t > &) |
| L^2 scalarproduct of two fields on sphere. | |
| GReal_t | H2S2 (const ScalarFieldMP< GReal_t > &, const ScalarFieldMP< GReal_t > &, const int mu) |
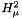 Sobolev scalarproduct of two fields on sphere. Sobolev scalarproduct of two fields on sphere. | |
| ScalarFieldMP< GReal_t > | reflect (const ScalarFieldMP< GReal_t > &) |
| Reflect with respect to origin (parity operator). | |
| ScalarFieldMP< GReal_t > | mulCosTheta (const ScalarFieldMP< GReal_t > &) |
Multiplication operator by 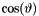 . . | |
| ScalarFieldMP< GReal_t > | mulCosThetaSqr (const ScalarFieldMP< GReal_t > &) |
Multiplication operator by 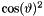 . . | |
| ScalarFieldMP< GReal_t > | mulSinThetaSqr (const ScalarFieldMP< GReal_t > &) |
Multiplication operator by 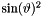 . . | |
| ScalarFieldMP< GReal_t > | partial_phi (const ScalarFieldMP< GReal_t > &) |
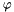 derivative on sphere for real scalar field. derivative on sphere for real scalar field. | |
| ScalarFieldMP< GReal_t > | Sqr_partial_phi (const ScalarFieldMP< GReal_t > &) |
Second 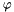 derivative on sphere for real scalar field. derivative on sphere for real scalar field. | |
| ScalarFieldMP< GReal_t > | sinTheta_partial_theta (const ScalarFieldMP< GReal_t > &) |
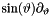 derivative on sphere for real scalar field. derivative on sphere for real scalar field. | |
| ScalarFieldMP< GReal_t > | partial_x (const ScalarFieldMP< GReal_t > &) |
( 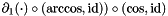 derivative on sphere for real scalar field. derivative on sphere for real scalar field. | |
| ScalarFieldMP< GReal_t > | LaplaceS2 (const ScalarFieldMP< GReal_t > &) |
| Laplace operator on unit sphere for real scalar field. | |
| GReal_t | normBoundNeumann (const GReal_t a00, const GReal_t H2S2aa) |
Upper estimate of the 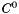 norm of norm of 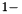 a real field for Neumann series expansion. a real field for Neumann series expansion. | |
| GReal_t | optimalScalingNeumann (const GReal_t a00, const GReal_t H2S2aa) |
Scaling factor 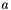 , with which , with which 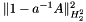 is minimized for a real field is minimized for a real field 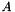 on sphere. on sphere. | |
| ScalarFieldMP< GReal_t > | divideByNeumann (const ScalarFieldMP< GReal_t > &a, const ScalarFieldMP< GReal_t > &f, const GReal_t norm, const GReal_t errortolerance) |
| Division of a real field by a real field, using Neumann series. | |
| GReal_t | tailErrorBoundS2 (const ScalarFieldMP< GReal_t > &, const int mup, const int mu, int *lmax, int *mmax) |
An upper bound for the tail sum in 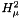 norm, assuming that the field is in the space norm, assuming that the field is in the space 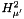 . . | |
| ScalarFieldMP< GComplex_t > | operator+ (const ScalarFieldMP< GComplex_t > &, const ScalarFieldMP< GComplex_t > &) |
| ScalarFieldMP<GComplex_t> algebraic operators. | |
| ScalarFieldMP< GComplex_t > | operator+ (const ScalarFieldMP< GComplex_t > &, const ScalarFieldMP< GReal_t > &) |
| ScalarFieldMP< GComplex_t > | operator+ (const ScalarFieldMP< GReal_t > &, const ScalarFieldMP< GComplex_t > &) |
| ScalarFieldMP< GComplex_t > | operator- (const ScalarFieldMP< GComplex_t > &, const ScalarFieldMP< GComplex_t > &) |
| ScalarFieldMP< GComplex_t > | operator- (const ScalarFieldMP< GComplex_t > &, const ScalarFieldMP< GReal_t > &) |
| ScalarFieldMP< GComplex_t > | operator- (const ScalarFieldMP< GReal_t > &, const ScalarFieldMP< GComplex_t > &) |
| ScalarFieldMP< GComplex_t > | operator- (const ScalarFieldMP< GComplex_t > &) |
| ScalarFieldMP< GComplex_t > | operator* (const ScalarFieldMP< GComplex_t > &, const GReal_t) |
| ScalarFieldMP< GComplex_t > | operator* (const GReal_t, const ScalarFieldMP< GComplex_t > &) |
| ScalarFieldMP< GComplex_t > | operator* (const ScalarFieldMP< GComplex_t > &, const GComplex_t &) |
| ScalarFieldMP< GComplex_t > | operator* (const GComplex_t &, const ScalarFieldMP< GComplex_t > &) |
| ScalarFieldMP< GComplex_t > | operator* (const ScalarFieldMP< GReal_t > &, const GComplex_t &) |
| ScalarFieldMP< GComplex_t > | operator* (const GComplex_t &, const ScalarFieldMP< GReal_t > &) |
| ScalarFieldMP< GComplex_t > | operator* (const ScalarFieldMP< GComplex_t > &, const ScalarFieldMP< GComplex_t > &) |
| ScalarFieldMP< GComplex_t > | operator* (const ScalarFieldMP< GComplex_t > &, const ScalarFieldMP< GReal_t > &) |
| ScalarFieldMP< GComplex_t > | operator* (const ScalarFieldMP< GReal_t > &, const ScalarFieldMP< GComplex_t > &) |
| ScalarFieldMP< GComplex_t > | operator/ (const ScalarFieldMP< GComplex_t > &, const GReal_t) |
| ScalarFieldMP< GComplex_t > | operator/ (const ScalarFieldMP< GComplex_t > &, const GComplex_t &) |
| ScalarFieldMP< GComplex_t > | operator/ (const ScalarFieldMP< GReal_t > &, const GComplex_t &) |
| ScalarFieldMP< GComplex_t > | conj (const ScalarFieldMP< GComplex_t > &) |
| Complex conjugate a scalarfield on sphere. | |
| ScalarFieldMP< GReal_t > | real (const ScalarFieldMP< GComplex_t > &) |
| Real part of a scalarfield on sphere. | |
| ScalarFieldMP< GReal_t > | imag (const ScalarFieldMP< GComplex_t > &) |
| Imaginary part of a scalarfield on sphere. | |
| GComplex_t | L2S2 (const ScalarFieldMP< GComplex_t > &, const ScalarFieldMP< GReal_t > &) |
| L^2 scalarproduct of fields. | |
| GComplex_t | L2S2 (const ScalarFieldMP< GReal_t > &, const ScalarFieldMP< GComplex_t > &) |
| GComplex_t | L2S2 (const ScalarFieldMP< GComplex_t > &, const ScalarFieldMP< GComplex_t > &) |
| GComplex_t | H2S2 (const ScalarFieldMP< GComplex_t > &, const ScalarFieldMP< GReal_t > &, const int mu) |
 Sobolev scalarproduct of two fields on sphere. Sobolev scalarproduct of two fields on sphere. | |
| GComplex_t | H2S2 (const ScalarFieldMP< GReal_t > &, const ScalarFieldMP< GComplex_t > &, const int mu) |
| GComplex_t | H2S2 (const ScalarFieldMP< GComplex_t > &, const ScalarFieldMP< GComplex_t > &, const int mu) |
| GComplex_t | L2S2limited (const ScalarFieldMP< GComplex_t > &, const ScalarFieldMP< GComplex_t > &, const GReal_t theta, tvector< tvector< tvector< GReal_t > > > *coeffstorage) |
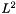 scalarproduct of fields, with limited integration domain to scalarproduct of fields, with limited integration domain to ![$[0,\theta]\times[0,2\pi]$](form_94.png) . . | |
| ScalarFieldMP< GComplex_t > | reflect (const ScalarFieldMP< GComplex_t > &) |
| Reflect with respect to origin (parity operator). | |
| ScalarFieldMP< GComplex_t > | stepping (const ScalarFieldMP< GComplex_t > &, const int upOrDown) |
| Stepping up and down operators. | |
| ScalarFieldMP< GComplex_t > | mulCosTheta (const ScalarFieldMP< GComplex_t > &) |
Multiplication operator by 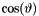 . . | |
| ScalarFieldMP< GComplex_t > | mulCosThetaSqr (const ScalarFieldMP< GComplex_t > &) |
Multiplication operator by 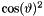 . . | |
| ScalarFieldMP< GComplex_t > | mulSinThetaSqr (const ScalarFieldMP< GComplex_t > &) |
Multiplication operator by 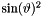 . . | |
| ScalarFieldMP< GComplex_t > | mulExpPmIPhi (const ScalarFieldMP< GComplex_t > &, const int sign) |
Multiplication operator by 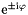 . . | |
| ScalarFieldMP< GComplex_t > | partial_phi (const ScalarFieldMP< GComplex_t > &) |
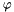 derivative on sphere for complex scalar field. derivative on sphere for complex scalar field. | |
| ScalarFieldMP< GComplex_t > | Sqr_partial_phi (const ScalarFieldMP< GComplex_t > &) |
Second 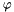 derivative on sphere for complex scalar field. derivative on sphere for complex scalar field. | |
| ScalarFieldMP< GComplex_t > | sinTheta_partial_theta (const ScalarFieldMP< GComplex_t > &) |
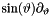 derivative on sphere for complex scalar field. derivative on sphere for complex scalar field. | |
| ScalarFieldMP< GComplex_t > | partial_theta (const ScalarFieldMP< GComplex_t > &) |
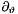 derivative on sphere for complex field. derivative on sphere for complex field. | |
| ScalarFieldMP< GComplex_t > | partial_x (const ScalarFieldMP< GComplex_t > &) |
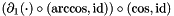 derivative on sphere for complex scalar field. derivative on sphere for complex scalar field. | |
| ScalarFieldMP< GComplex_t > | LaplaceS2 (const ScalarFieldMP< GComplex_t > &) |
| Laplace operator on unit sphere for complex scalar field. | |
| GReal_t | normBoundNeumann (const GComplex_t &a00, const GComplex_t &H2S2aa) |
Upper estimate of the 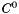 norm of norm of  a complex field for Neumann series. a complex field for Neumann series. | |
| GComplex_t | optimalScalingNeumann (const GComplex_t &a00, const GComplex_t &H2S2aa) |
Scaling factor 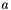 , with which , with which 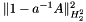 is minimized for a complex field $A$ on sphere. is minimized for a complex field $A$ on sphere. | |
| ScalarFieldMP< GComplex_t > | divideByNeumann (const ScalarFieldMP< GComplex_t > &a, const ScalarFieldMP< GReal_t > &f, const GReal_t norm, const GReal_t errortolerance) |
| Division of a complex field by a complex field, using Neumann series. | |
| ScalarFieldMP< GComplex_t > | divideByNeumann (const ScalarFieldMP< GReal_t > &a, const ScalarFieldMP< GComplex_t > &f, const GReal_t norm, const GReal_t errortolerance) |
| ScalarFieldMP< GComplex_t > | divideByNeumann (const ScalarFieldMP< GComplex_t > &a, const ScalarFieldMP< GComplex_t > &f, const GReal_t norm, const GReal_t errortolerance) |
| GReal_t | tailErrorBoundS2 (const ScalarFieldMP< GComplex_t > &a, const int mup, const int mu, int *lmax, int *mmax) |
An upper bound for the tail sum in the 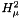 norm, assuming that the field is in the space norm, assuming that the field is in the space 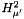 . . | |
| void | maxEval (const unsigned int) |
| Integration error tolerance parameters for functional field expansion by AGM routine. | |
| unsigned int | maxEval () |
| void | reqAbsError (const GReal_t) |
| GReal_t | reqAbsError () |
| void | reqRelError (const GReal_t) |
| GReal_t | reqRelError () |
Variables | |
| const int | SobolevOrderS2 = 1000000 |
| Maximal series expansion order for the numerical calculation of Sobolev related constants over the sphere. | |
Detailed Description
Multipole expansion classes and methods.
Function Documentation
| Coeff<GComplex_t> gridripper::multipole::conj | ( | const Y & | ) |
Complex conjugate a coefficient.
| ScalarFieldMP<GComplex_t> gridripper::multipole::conj | ( | const ScalarFieldMP< GComplex_t > & | ) |
Complex conjugate a scalarfield on sphere.
Based on: 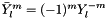 .
.
| ScalarFieldMP<GComplex_t> gridripper::multipole::divideByNeumann | ( | const ScalarFieldMP< GComplex_t > & | a, | |
| const ScalarFieldMP< GReal_t > & | f, | |||
| const GReal_t | norm, | |||
| const GReal_t | errortolerance | |||
| ) |
Division of a complex field by a complex field, using Neumann series.
Based on: 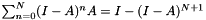 , where
, where 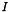 is the identity operator and
is the identity operator and 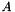 is such an operator that
is such an operator that 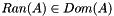 . Specially, if
. Specially, if 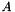 is continuous, then it is absolute convergent if and only if
is continuous, then it is absolute convergent if and only if 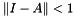 , furthermore
, furthermore 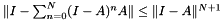 . If
. If 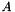 is a multiplication by a measurable function
is a multiplication by a measurable function 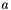 , then equality holds instead of inequality, and
, then equality holds instead of inequality, and 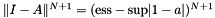 .
.
- Parameters:
-
a : the field, which is in the nominator f : the field to be divided norm : an estimate for the essential supremum of 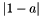
tolerance : an error tolarance
- Returns:
- f/a : up to the specified error tolerance
| ScalarFieldMP<GReal_t> gridripper::multipole::divideByNeumann | ( | const ScalarFieldMP< GReal_t > & | a, | |
| const ScalarFieldMP< GReal_t > & | f, | |||
| const GReal_t | norm, | |||
| const GReal_t | errortolerance | |||
| ) |
Division of a real field by a real field, using Neumann series.
Based on: same rule as for complex.
| GReal_t gridripper::multipole::ExpPmIPhiYY_coupling | ( | const int | l1, | |
| const int | m1, | |||
| const int | l2, | |||
| const int | sign | |||
| ) |
The overlap integrals 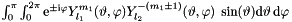 .
.
Based on: idea from J. Phys. A31 (1998) 1101, and J. Phys. A32 (1999) 2601, and J. Phys. A35 (2002) 4187. Namely, on expanding of products of Y-s by Gaunt coefficients 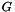 .
. 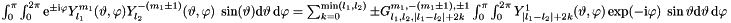 . This quantity is zero for: 1)
. This quantity is zero for: 1)  or
or 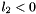 , 2)
, 2) 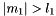 or
or 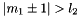 , 3)
, 3) 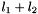 even.
even.
Numerically verified using a Maple code.
- Version:
- 0.5, 04/01/2008
- Since:
- GridRipper 0.5
| unsigned int gridripper::multipole::ExpPmIPhiYY_coupling_size | ( | ) |
Show table size currently used in ExpPmIPhiYY_coupling.
| ScalarFieldMP<GReal_t> gridripper::multipole::imag | ( | const ScalarFieldMP< GComplex_t > & | ) |
Imaginary part of a scalarfield on sphere.
| GReal_t gridripper::multipole::intBarYl1mYl2m | ( | const int | l1, | |
| const int | l2, | |||
| const int | m, | |||
| const GReal_t | theta, | |||
| tvector< tvector< tvector< GReal_t > > > * | coeffstorage | |||
| ) |
Calculation of ![$\int_{[0,\theta]\times[0,2\pi]} \bar{Y}_{l_1}^{m} Y_{l_2}^{m} \;\mathrm{d}\lambda_{S^2}$](form_58.png) .
.
Based on: expansion of 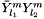 product by using Gaunt coefficients. Result:
product by using Gaunt coefficients. Result: ![$\int_{[0,\theta]\times[0,2\pi]} \bar{Y}_{l_1}^{m} Y_{l_2}^{m} \;\mathrm{d}\lambda_{S^2} = (-1)^{m} \sum_{k=0}^{\min(l_1, l_2)} G_{l_1,l_2,|l_1-l_2|+|l_1-l_2|\%2+2k}^{-m,m,0} \int_{[0,\theta]\times[0,2\pi]} Y_{|l_1-l_2|+|l_1-l_2|\%2+2k}^{0} \;\mathrm{d}\lambda_{S^2}$](form_60.png) ,
, 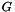 being the Gaunt coefficients.
being the Gaunt coefficients.
To avoid expensive evaluation, a table is stored (appended) to 'coeffstorage'. Initially should be empty, and should be different for every ' 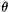 '. If the pointer to 'coeffstorage' is NULL, the coefficients are not stored, but calculated each time.
'. If the pointer to 'coeffstorage' is NULL, the coefficients are not stored, but calculated each time.
Numerically verified using Maple.
- Version:
- 0.5, 22/07/2008
- Since:
- GridRipper 0.5
| GReal_t gridripper::multipole::intYl0 | ( | const int | l, | |
| const GReal_t | theta | |||
| ) |
Calculation of ![$\int_{[0,\theta]\times[0,2\pi]} Y_{l}^{0} \;\mathrm{d}\lambda_{S^2}$](form_55.png) .
.
Based on: 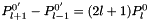 (from Journal of Modern Optics 36 (1989) 685, but may be easily verified from Rodriguez formula). Result is:
(from Journal of Modern Optics 36 (1989) 685, but may be easily verified from Rodriguez formula). Result is: ![$\int_{[0,\theta]\times[0,2\pi]} Y_{l}^{0} \;\mathrm{d}\lambda_{S^2} = 2\pi ( \frac{1}{\sqrt{4\pi}}\delta_{l,0} - \frac{1}{\sqrt{(2l+1)(2l+3)}}Y_{l+1}^{0}(\theta, 0) + \frac{1}{\sqrt{(2l-1)(2l+1)}}Y_{l-1}^{0}(\theta, 0) )$](form_57.png) .
.
Numerically verified using Maple.
- Version:
- 0.5, 22/07/2008
- Since:
- GridRipper 0.5
| GReal_t gridripper::multipole::intYl1ExpMIPhi | ( | const int | l | ) |
Calculation of 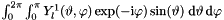 .
.
Based on: formula in J. Phys. A32 (1999) 2601. Namely: 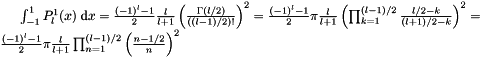 delivers final result (which is zero for even
delivers final result (which is zero for even 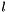 ). Thus:
). Thus: 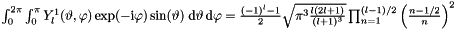 delivers final result (which is zero for even
delivers final result (which is zero for even 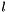 ).
).
Numerically verified using a Maple and Mathematica code.
- Version:
- 0.5, 04/01/2008
- Since:
- GridRipper 0.5
| GComplex_t gridripper::multipole::L2S2 | ( | const ScalarFieldMP< GComplex_t > & | , | |
| const ScalarFieldMP< GReal_t > & | ||||
| ) |
L^2 scalarproduct of fields.
Based on: 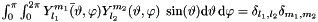 .
.
| GReal_t gridripper::multipole::L2S2 | ( | const ScalarFieldMP< GReal_t > & | , | |
| const ScalarFieldMP< GReal_t > & | ||||
| ) |
L^2 scalarproduct of two fields on sphere.
Based on: 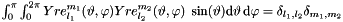 .
.
| GComplex_t gridripper::multipole::L2S2limited | ( | const ScalarFieldMP< GComplex_t > & | , | |
| const ScalarFieldMP< GComplex_t > & | , | |||
| const GReal_t | theta, | |||
| tvector< tvector< tvector< GReal_t > > > * | coeffstorage | |||
| ) |
 scalarproduct of fields, with limited integration domain to
scalarproduct of fields, with limited integration domain to ![$[0,\theta]\times[0,2\pi]$](form_94.png) .
.
Based on the Gaunt expansion of spherical harmonic products. (See Gaunt.h and Gaunt.cxx.) The necessary coefficient matrix is stored (appended) to 'coeffstorage', for a given ' 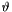 '. Should be empty initially for a given '
'. Should be empty initially for a given ' 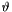 '. If the pointer to 'coeffstorage' is NULL, the coefficient matrix is not stored in table, but calculated every time.
'. If the pointer to 'coeffstorage' is NULL, the coefficient matrix is not stored in table, but calculated every time.
| ScalarFieldMP<GReal_t> gridripper::multipole::LaplaceS2 | ( | const ScalarFieldMP< GReal_t > & | ) |
Laplace operator on unit sphere for real scalar field.
Based on: 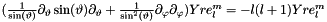 .
.
| ScalarFieldMP<GComplex_t> gridripper::multipole::LaplaceS2 | ( | const ScalarFieldMP< GComplex_t > & | ) |
Laplace operator on unit sphere for complex scalar field.
Based on: 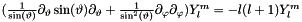 .
.
| ScalarFieldMP<GComplex_t> gridripper::multipole::mulCosTheta | ( | const ScalarFieldMP< GComplex_t > & | ) |
Multiplication operator by 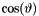 .
.
Based on:  . Numerically verified by a C++ code.
. Numerically verified by a C++ code.
| ScalarFieldMP<GReal_t> gridripper::multipole::mulCosTheta | ( | const ScalarFieldMP< GReal_t > & | ) |
Multiplication operator by 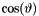 .
.
Based on the rule for Y basis. Numerically verified using a C++ code.
| ScalarFieldMP<GComplex_t> gridripper::multipole::mulCosThetaSqr | ( | const ScalarFieldMP< GComplex_t > & | ) |
Multiplication operator by 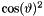 .
.
Based on: 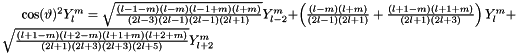 . Numerically verified by a C++ code.
. Numerically verified by a C++ code.
| ScalarFieldMP<GReal_t> gridripper::multipole::mulCosThetaSqr | ( | const ScalarFieldMP< GReal_t > & | ) |
Multiplication operator by 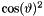 .
.
Based on the rule for Y basis. Numerically verified using a C++ code.
| ScalarFieldMP<GComplex_t> gridripper::multipole::mulExpPmIPhi | ( | const ScalarFieldMP< GComplex_t > & | , | |
| const int | sign | |||
| ) |
Multiplication operator by 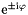 .
.
Based on: matrix elements is Gaunt.h, Gaunt.cxx. Numerically verified by a Maple code.
| ScalarFieldMP<GComplex_t> gridripper::multipole::mulSinThetaSqr | ( | const ScalarFieldMP< GComplex_t > & | ) |
Multiplication operator by 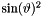 .
.
Based on: 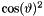 . Numerically verified by a C++ code.
. Numerically verified by a C++ code.
| ScalarFieldMP<GReal_t> gridripper::multipole::mulSinThetaSqr | ( | const ScalarFieldMP< GReal_t > & | ) |
Multiplication operator by 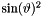 .
.
Based on: 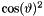 . Numerically verified using a C++ code.
. Numerically verified using a C++ code.
| GReal_t gridripper::multipole::normBoundNeumann | ( | const GComplex_t & | a00, | |
| const GComplex_t & | H2S2aa | |||
| ) |
Upper estimate of the  norm of
norm of  a complex field for Neumann series.
a complex field for Neumann series.
Based on: the Sobolev inequality, namely 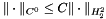 .
.
- Parameters:
-
a00 : the (0, 0) multipole component of the field H2S2aa : the 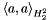 scalar product
scalar product
| GReal_t gridripper::multipole::normBoundNeumann | ( | const GReal_t | a00, | |
| const GReal_t | H2S2aa | |||
| ) |
Upper estimate of the 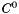 norm of
norm of 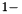 a real field for Neumann series expansion.
a real field for Neumann series expansion.
Based on: the 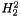 Sobolev inequality, namely
Sobolev inequality, namely 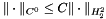 .
.
- Parameters:
-
a00 : the (0, 0) multipole component of the field H2S2aa : the 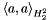 scalar product
scalar product
| Coeff<GReal_t> gridripper::multipole::operator* | ( | const | GReal_t, | |
| const Coeff< GReal_t > & | ||||
| ) |
Multiply a coefficient by a number.
| Coeff<GReal_t> gridripper::multipole::operator* | ( | const | GReal_t, | |
| const Yre & | ||||
| ) |
Tensor product of a number and an Yre.
| Coeff<GComplex_t> gridripper::multipole::operator* | ( | const | GReal_t, | |
| const Y & | ||||
| ) |
Tensor product of a number and an Y.
| Coeff<GComplex_t> gridripper::multipole::operator* | ( | const | GReal_t, | |
| const Coeff< GComplex_t > & | ||||
| ) |
Multiply a coefficient by a number.
| ScalarFieldMP<GReal_t> gridripper::multipole::operator+ | ( | const ScalarFieldMP< GReal_t > & | , | |
| const ScalarFieldMP< GReal_t > & | ||||
| ) |
ScalarFieldMP<GReal_t> algebraic operators.
| ScalarFieldMP<GComplex_t> gridripper::multipole::operator+ | ( | const ScalarFieldMP< GComplex_t > & | , | |
| const ScalarFieldMP< GComplex_t > & | ||||
| ) |
ScalarFieldMP<GComplex_t> algebraic operators.
| Coeff<GReal_t> gridripper::multipole::operator- | ( | const Yre & | ) |
Negative of a coefficient.
| Coeff<GComplex_t> gridripper::multipole::operator- | ( | const Y & | ) |
Negative of a coefficient.
| Coeff<GComplex_t> gridripper::multipole::operator/ | ( | const Coeff< GComplex_t > & | , | |
| const | GReal_t | |||
| ) |
Divide a coefficient by a number.
| Coeff<GReal_t> gridripper::multipole::operator/ | ( | const Yre & | , | |
| const | GReal_t | |||
| ) |
Tensor quotient of a number and an Yre.
| Coeff<GReal_t> gridripper::multipole::operator/ | ( | const Coeff< GReal_t > & | , | |
| const | GReal_t | |||
| ) |
Divide a coefficient by a number.
| Coeff<GComplex_t> gridripper::multipole::operator/ | ( | const Y & | , | |
| const | GReal_t | |||
| ) |
Tensor quotient of a number and an Y.
| GReal_t gridripper::multipole::optimalScalingNeumann | ( | const GReal_t | a00, | |
| const GReal_t | H2S2aa | |||
| ) |
Scaling factor 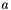 , with which
, with which 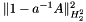 is minimized for a real field
is minimized for a real field 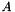 on sphere.
on sphere.
It is: 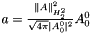 .
.
- Parameters:
-
a00 : the (0, 0) multipole component of the field H2S2aa : the 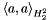 scalar product
scalar product
| GComplex_t gridripper::multipole::optimalScalingNeumann | ( | const GComplex_t & | a00, | |
| const GComplex_t & | H2S2aa | |||
| ) |
Scaling factor 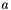 , with which
, with which 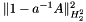 is minimized for a complex field $A$ on sphere.
is minimized for a complex field $A$ on sphere.
It is: 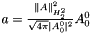 .
.
- Parameters:
-
a00 : the (0, 0) multipole component of the field H2S2aa : the 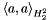 scalar product
scalar product
| ScalarFieldMP<GReal_t> gridripper::multipole::partial_phi | ( | const ScalarFieldMP< GReal_t > & | ) |
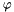 derivative on sphere for real scalar field.
derivative on sphere for real scalar field.
Based on: 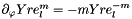 .
.
| ScalarFieldMP<GComplex_t> gridripper::multipole::partial_phi | ( | const ScalarFieldMP< GComplex_t > & | ) |
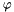 derivative on sphere for complex scalar field.
derivative on sphere for complex scalar field.
Based on: 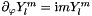 .
.
| ScalarFieldMP<GComplex_t> gridripper::multipole::partial_theta | ( | const ScalarFieldMP< GComplex_t > & | ) |
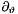 derivative on sphere for complex field.
derivative on sphere for complex field.
Based on the stepping operators and on the matrix elements of the multiplication operator by 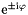 (Gaunt.h and Gaunt.cxx). Numerically verified by a Maple code.
(Gaunt.h and Gaunt.cxx). Numerically verified by a Maple code.
| ScalarFieldMP<GComplex_t> gridripper::multipole::partial_x | ( | const ScalarFieldMP< GComplex_t > & | ) |
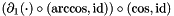 derivative on sphere for complex scalar field.
derivative on sphere for complex scalar field.
(' 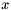 '-derivative,
'-derivative, 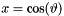 .) From Journal of Modern Optics 36 (1989) 685:
.) From Journal of Modern Optics 36 (1989) 685: 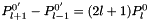 (easily verified from Rodriguez formula). Thus:
(easily verified from Rodriguez formula). Thus: 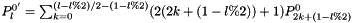 . Thus:
. Thus: 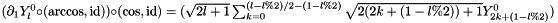 . Not implemented for
. Not implemented for 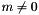 . Not even all
. Not even all 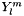 is in its domain in the
is in its domain in the 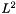 sense. Numerically verified using a C++ code.
sense. Numerically verified using a C++ code.
| ScalarFieldMP<GReal_t> gridripper::multipole::partial_x | ( | const ScalarFieldMP< GReal_t > & | ) |
( 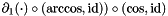 derivative on sphere for real scalar field.
derivative on sphere for real scalar field.
(' 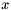 '-derivative,
'-derivative, 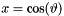 .) Based on the rule for Y basis. Not implemented for
.) Based on the rule for Y basis. Not implemented for 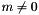 . Not even all
. Not even all 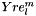 is in its domain in the L^2 sense if
is in its domain in the L^2 sense if 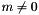 . Numerically verified using a C++ code.
. Numerically verified using a C++ code.
| ScalarFieldMP<GReal_t> gridripper::multipole::real | ( | const ScalarFieldMP< GComplex_t > & | ) |
Real part of a scalarfield on sphere.
| ScalarFieldMP<GReal_t> gridripper::multipole::reflect | ( | const ScalarFieldMP< GReal_t > & | ) |
Reflect with respect to origin (parity operator).
Based on: 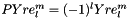 .
.
| ScalarFieldMP<GComplex_t> gridripper::multipole::reflect | ( | const ScalarFieldMP< GComplex_t > & | ) |
Reflect with respect to origin (parity operator).
Based on: 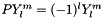 .
.
| ScalarFieldMP<GComplex_t> gridripper::multipole::sinTheta_partial_theta | ( | const ScalarFieldMP< GComplex_t > & | ) |
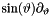 derivative on sphere for complex scalar field.
derivative on sphere for complex scalar field.
Based on: 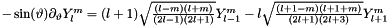 . Numerically verified using a C++ code.
. Numerically verified using a C++ code.
| ScalarFieldMP<GReal_t> gridripper::multipole::sinTheta_partial_theta | ( | const ScalarFieldMP< GReal_t > & | ) |
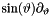 derivative on sphere for real scalar field.
derivative on sphere for real scalar field.
Based on the rule for Y basis. Numerically verified using a C++ code.
| GReal_t gridripper::multipole::SobolevConstantS2 | ( | const int | m | ) |
The minimal Sobolev constant in the inequality over the sphere: 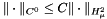 .
.
It is the sum 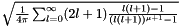 .
.
| ScalarFieldMP<GReal_t> gridripper::multipole::Sqr_partial_phi | ( | const ScalarFieldMP< GReal_t > & | ) |
Second 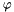 derivative on sphere for real scalar field.
derivative on sphere for real scalar field.
Based on: 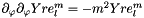 .
.
| ScalarFieldMP<GComplex_t> gridripper::multipole::Sqr_partial_phi | ( | const ScalarFieldMP< GComplex_t > & | ) |
Second 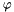 derivative on sphere for complex scalar field.
derivative on sphere for complex scalar field.
Based on: 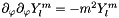 .
.
| ScalarFieldMP<GComplex_t> gridripper::multipole::stepping | ( | const ScalarFieldMP< GComplex_t > & | , | |
| const int | upOrDown | |||
| ) |
Stepping up and down operators.
Based on: 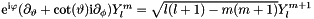 (stepping up,
(stepping up,  operator).
operator). 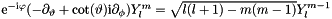 (stepping down,
(stepping down, 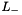 operator).
operator).
Numerically verified using a C++ code.
| GReal_t gridripper::multipole::tailErrorBoundS2 | ( | const ScalarFieldMP< GReal_t > & | , | |
| const int | mup, | |||
| const int | mu, | |||
| int * | lmax, | |||
| int * | mmax | |||
| ) |
An upper bound for the tail sum in 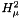 norm, assuming that the field is in the space
norm, assuming that the field is in the space 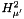 .
.
Based on: same rule for complex.
| GReal_t gridripper::multipole::tailErrorBoundS2 | ( | const ScalarFieldMP< GComplex_t > & | a, | |
| const int | mup, | |||
| const int | mu, | |||
| int * | lmax, | |||
| int * | mmax | |||
| ) |
An upper bound for the tail sum in the 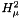 norm, assuming that the field is in the space
norm, assuming that the field is in the space 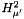 .
.
In this case, its multipole coefficients may be bound by the sequence 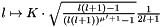 . By adjusting
. By adjusting 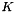 to the stored coefficients, and by summing up the tail of this bound in the
to the stored coefficients, and by summing up the tail of this bound in the 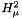 norm, one gets an upper estimate for the
norm, one gets an upper estimate for the 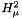 norm of the tail error.
norm of the tail error.
| GReal_t gridripper::multipole::YreYreYre_coupling | ( | const int | l1, | |
| const int | l2, | |||
| const int | l3, | |||
| const int | m1, | |||
| const int | m2, | |||
| const int | m3 | |||
| ) |
The same coupling for Yre basis.
They are real valued as Yre -s are real valued. Zero if not: 1) 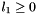 and
and 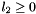 and
and 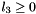 , and 2)
, and 2) 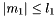 and
and 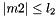 and
and 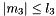 , and 3)
, and 3) 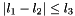 and
and 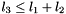 , and 4) only zero or two of the
, and 4) only zero or two of the 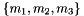 are negative, and 5)
are negative, and 5) 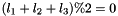 . See Bases.h for definition of Yre basis.
. See Bases.h for definition of Yre basis.
Not tested numerically. Not used so far in multiplication operator.
- Version:
- 0.5, 01/31/2007
- Since:
- GridRipper 0.5
| GComplex_t gridripper::multipole::YYreY_coupling | ( | const int | l1, | |
| const int | l2, | |||
| const int | l3, | |||
| const int | m1, | |||
| const int | m2, | |||
| const int | m3 | |||
| ) |
| GReal_t gridripper::multipole::YYY_coupling | ( | const int | l1, | |
| const int | l2, | |||
| const int | l3, | |||
| const int | m1, | |||
| const int | m2, | |||
| const int | m3 | |||
| ) |
The  spherical harmonic function Gaunt coefficient calculator routine.
spherical harmonic function Gaunt coefficient calculator routine.
Zero if not: 1) 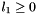 and
and 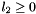 and
and 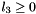 , and 2)
, and 2) 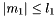 and
and 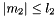 and
and 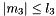 , and 3)
, and 3) 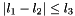 and
and 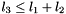 , and 4)
, and 4) 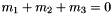 , and 5)
, and 5) 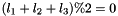 . Thus, by 4), they are real valued, which is not obvious otherwise. See Bases.h for definition of Y basis.
. Thus, by 4), they are real valued, which is not obvious otherwise. See Bases.h for definition of Y basis.
Numerically verified using Maple.
- Version:
- 0.5, 01/31/2007
- Since:
- GridRipper 0.5
| unsigned int gridripper::multipole::YYY_coupling_size | ( | ) |
Show table size currently used in YYY_coupling.
| bool gridripper::multipole::YYY_coupling_zeros | ( | const int | l1, | |
| const int | l2, | |||
| const int | l3, | |||
| const int | m1, | |||
| const int | m2, | |||
| const int | m3 | |||
| ) |
Returns true if the Gaunt coefficient of given index is known to be zero.
I.e. returns true if the output of YYY_coupling is not needed to be stored, as it will be zero anyway.
Numerically verified using Maple.
- Version:
- 1.0, 22/04/2011
- Since:
- GridRipper 1.0
 , and 5)
, and 5)  1.7.1
1.7.1