Originally: KFKI-1998-02/C

 

 

 

 

 

 

 

 

BETWEEN EDUCATED GUESS AND PROOF: PHENOMENA AT THE BORDERLINE OF STATISTICS

 

B. Lukács

 

Central Research Institute for Physics RMKI, H-1525 Bp. 114. Pf. 49.

 

ABSTRACT

            5 different problems are investigated where the statistics is very poor but the number of measurements cannot be increased, at least in this moment. Special techniques, however, help moderately. The problems are: Lower Miocene sunspot cycles from annual ring patterns, connection between prices and sunspot relative numbers, spurious scattering, the chronology of early Sumerian kings and the pattern of archaic Chinese verses.

 

1. INTRODUCTION

            Philosophers and historians of science classify science; scientists do it. The formers often tell that the domain of natural sciences (or physics) is phenomena which can be observed in prepared circumstances, which can be repeated without limit. Then one can distinguish accidents from rules.

            Indeed, the rules of free fall can be investigated in various environments. The experimenter can be male, female or a machine; can be young or old and in any mental state. So if one tried with a unified theory in which stones fell faster from the hand of a woman than of a man, it could be checked within days. (And if one regards such an idea far-fetched, remember Rhine's famous results where suggestive persons were reported to cause more 6's on dices than the layman.)

            The life of physicists would be very easy if all phenomena were repeatable. However it is not so. Consider SN 1987A in the Large Magellan Cloud. It was almost galactic, so lots of details were observable. Such an event is expected once in 300 years, and we cannot prepare the circumstances.

            There are two correct attitudes. We may say that unrepeatable phenomena do not belong to physics and physicists have to ignore them. This standpoint is methodically consequent; but what if the phenomenon is important? Or we may turn to the important unrepeatable phenomena and try to do something with them. This standpoint is constructive, but methodically awkward.

            Everybody can choose. In the first case nothing is to be done, which is a simple task. In the second it is not clear how to proceed; but at the end there may be some result. Only, the result may be not fully significant; but a result significant on 90 % level is better than no result at all.

            The problem is generally with the statistics. If we cannot repeat a measurement, then statistical mean deviations cannot be reduced in the standard way. The only way out (if it works at all) is to use special evaluation techniques; and even then the significance may remain limited.

            In this paper I am going to show 5 such cases, from various topics. In each case full certainty is not at reach, but a partial answer has been obtained.

            There is a Lower Miocene tree trunk in Hungary in such a good preservation that a cca. 7 year "periodicity" is seen in the annual ring pattern. Is the 7 years the Lower Miocene sunspot cycle, or a statistic fluctuation? Unfortunately, this one trunk is available and the tree died very early.

            There seems to be a slight correlation between prices and sunspot numbers, at least in England. A larger statistics would be welcome, but how to reconstruct sunspot relative numbers before the first telescope of Galileo?

            There seems to be an effect seen on particle tracks in photoemulsions, called spurious scattering. It was believed by Jánossy to be an unorthodox quantum effect, and it may be a Quantum Gravity effect. Does it really exist? Unfortunately, emulsions are going out of fashion, and the old high-atmosphere techniques giving the data as byproducts are obsolete for many decades, while many old data were lost with the many generational changes of computer technology.

            World's oldest kings are listed only on one list, 4000 year old, giving absurd data. Can we find out anything from statements that they ruled for centuries, or not? And the statistics cannot be improved. There was as many kings as there was.

            China's oldest verses are strange. There is a theory, what specific structure made them just verses for archaic Chinese, but we cannot ask archaic Chinese, and so far no archaic Chinese theoretical work has turned up about them.

            In each case, however, something can be done. The result is maybe not full proof; but what happens if somebody is only 90 % certain about the patterns of archaic Chinese verses?

 

2. THE KAINOZOIC SUN

            In the last century antics of paleoclimate were explained via a changing Sun. Such an explanation was natural: nobody was sure what heats Sun, and the only available theory, contraction and Virial heating, predicted a 30 My past history [1]. Then Sun might have been quite different in the times of big reptiles.

            From 1945 it has been known that Sun is heated up by H‑>He fusion. According to calculations the fuel lasts some 10 Gy [2]. Since the whole phanerozoic is 560 My, it seemed that paleontology should be explained in the light of a Sun quite indistinguishable from the present one. Then the extinction of dinosaurs was explained via continental drifts, breakup of a continuous cloud layer &c., and the Permian ice ages via unfortunate perturbations on Earth's orbit, intrusion of interstellar dust and so on.

            In 1972, however, Fowler showed a possibility of a cyclic evolution of Sun [3]. For a time H is converted into He in the core. Particle number is decreasing, but pressure must not, so temperature is rising. Then the fusion rate is growing. This is a circulus vitiosus, but only for a while. When the temperature gradient becomes too high at the border of the core, convection starts and the excess He leaves the core. There the temperature and so fusion rate drop, and the cycle restarts. If so, then the cycles contain longer intervals of growing luminosity and shorter periods of fainter Sun. We can guess the cycle length as 200-250 My, which is the time from Permian to the present. Indeed, a continuous cooling is seen in the layers of the last 30 My, which is just the Kelvin-Helmholtz time of heating by contraction; the cooling Sun naturally contracts.

            From the previous experiences one can think that this is not necessarily the last word of astrophysics, and it would be good to check the "predictions". However we cannot directly observe the past Sun. Still, fossils tell something. It is sure, e.g., that from Cambrian the terrestrial mean temperature was never below 0 C°.

            Total luminosity is not the only characteristics of solar activity influencing terrestrial life (although it is the most important one). There is a semi-random fluctuation, manifested in flares, magnetic disturbances, solar wind irregularities, boreal aurorae, &c., whose most visible measure is the sunspot relative number (SRN). In our centuries the SRN exhibits a 11 year asymmetric cycle, with serious mean deviation in the length, and with longer trends too. (Details will be seen in the next Chapter.) There is no adequate explanation for just this 11 years, although qualitative models do exist. (For the problems see [4].) However it is natural to assume that the bulk properties of Sun determine the cycle length. Then in historic and prehistoric times the mean cycle length must have been also 11 years. Indeed, many old trees exhibit annual ring patterns with some cca. 11 year periodicity. It is rather hard to tell how and why sunspots influence trees (hither we will return too in the next Chapter), but for a while let us accept that they do somehow. However tree rings go back slightly beyond 7000 years and no more.

            Except for some fossils of exceptionally good preservation. One of them is the Ipolytarnóc pine trunk of Pinuxylon tarnocziense Tuzson Greguss from Lower Miocene. Ipolytarnóc is at the northeastern part of the central lowland region of the Carpathian Basin, and in the Lower Miocene (cca. -23 My) the site was a subtropic seashore. Humidity, temperature &c. were similar to those of present Assam.

            Now observe that, if Fowler is right, Miocene might have been the time of the latest solar change, so there is a possibility that the cycle of solar activity was different from 11 years just then. (Oligocene trunks would be better, but such finds are rare.) So the ring pattern of the Ipolytarnóc trunk may tell something important about astrophysics. Indeed, the preservation is so good that the ring pattern is clearly observable [5].

            Ref. 5 gave the full list of measured data, but the authors only guessed the cycle time from the distances of visible peaks: it was found to be cca. 7 years. However the consequences of such a result are so serious that a detailed statistical analysis is necessary. It is necessary, but rather hard. Namely, the tree died after 41 years; 38 rings can be evaluated. 38 data are generally insufficient for a statistical analysis: 1/Ö38 ~ 16 %, not much less than unity.

            But there are no more rings on this tree and there are no more trees from that site or from the Miocene of the Carpathian basin. So we may forget about the whole problem, or may try to use special methods. In Ref. 6 we did the second, and now I recapitulate the story.

            Our raw data are shown on Fig. 2.1: the individual error of measurement is estimated as 0.2 mm. However note that this error is not a white noise but rather strongly anticorrelated between neighbours, since the most difficult task is to find the exact border between neighbouring rings.

 

 

 

 

 

 

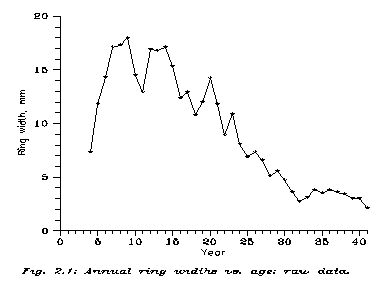
            The raw data show something; but not too much. They show that indeed the pine tree was suffering already in its very youth. We do not know, why; was it eaten in its vitals by a worm, or had its neighbours overgrown it, taking away from it the sunlight? It would be hard to tell.

            Now let us see why the authors of Ref. 5 claimed 7 year periodicity. Before computers there were popular smoothening methods of astronomers, which now we would call special moving averages. Now the measuring errors, causing a part of fluctuations, are strongly anticorrelated between neighbours, so let us smoothen just for neighbours. Let us call the raw data x(t), then

              y(t) º(x(t-1)+2x(t)+x(t+1))/4                                     

This is Fig. 2.2; it was published in Ref. 5, and indeed, if with some intuition, one identify not only peaks but shoulders as well, a periodicity with 6-7 years is seen. But the nontrivial trend in the data strongly influences the curve.

 

 

 

 

 

 

 

 

 

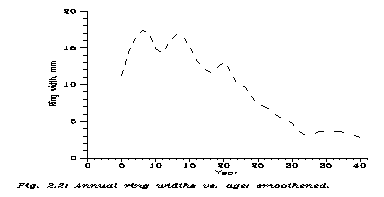
            Here let us stop for a moment. A tree of course does have a trend in its ring pattern, and it is sure that this trend has nothing common with sunspots. A very young tree grows slowly, because its roots are small, it does not get enough light between taller neighbours, and so on. An old tree grows slowly because most of its tissues are dead. Between that the tree shows some vigour. And: we are not at all interested in this trend. We are looking for fluctuations around the trend.

            Many times we will use correlation or autocorrelation analysis. Let us define the correlation r between two series; it will be autocorrelation if the second series is the same as the first, but shifted.

            Consider two discrete series of data of n elements, x_i(t) and y_i(t), respectively. Then <x> is the average and s_x is mean deviation of the series {x}.

              <x> º(1/n)å_ix_i                                                                                               (2.1)

              s_x² º(1/(n-1))å_i(x_i-<x>)²

Here s_x is the amplitude of fluctuations around <x>. Then the correlation coefficient r is defined as

              r º(n/(n-1))(<xy>-<x><y>)/s_xs_y                                                                    (2.2)

            Now, what is measured by r? It is easy to see that r takes its maximum if xºy, then it is 1 (the two series are fully correlated) and its minimum at yº-x, where it is -1 (the fluctuations move in totally opposite directions). For uncorrelated series r=0. The larger r² the larger correlation, i.e. connection (not necessarily direct). If we conjecture that x causes something on y, then it is worthwhile to calculate r with a delay time t, that is, between x(t) and y(t+t), because a propagation time is expected. This coefficient is denoted here by r_xy(t).

            Even two random series may produce some r via statistical fluctuation, but this accidental r decreases with increasing length n of the series. So r has a statistical error, which is, for correlated Gaussian distribution of x and y, given by

              s_r = (1-r²)/Ön                                                                                     (2.3)

and can be estimated by the same formula if the distribution is unknown. If in the measurement r²<s_r², for the true correlation r~0 is still quite possible. If the distribution of r is Gaussian or normal (which generally cannot be known if we do not have information about the correlation mechanism) then we know the significance limits.

            Let us see in more details the meaning of r. Take an example.

              x(t) = a(1+bsinWt)                                                                                          (2.4)

              y(t) = q(Y(t) + cx(t-t_o))

where a, b, c, q and W are constant, while Y randomly fluctuates with dispersion s. Then:

              r(t) = r_ocosW(t-t_o)                                                                                         (2.5)

where r_oºb/{b²+2s²/a²c²}^½. So c cancels in r if it is not very small, therefore r indeed measures the ratio of fluctuations of y dependent and independent of the change of x. If x(t) is only quasiperiodic, then  r(t) is only quasiperiodic too, and its exact form cannot be predicted without hypotheses for the mechanism leading to the correlation, although there is some similarity to the autocorrelation of x.

            Now, eqs. (2.4-5) show that r can extract very economically the common changes in two series. The sinusoideal nature is not important, mutatis mutandis the results would be similar with anything else instead of a sine, as far as its average is 0. However, the situation grossly changes if we multiply y(t) with a strongly time-dependent factor (I do not prove this, but everybody can try it by using ty(t) instead of y(t)). So it is better to remove the trend first.

            Now, what was the growth trend of our particular Ipolytarnóc palaeopine? Nobody knows; there is no available theory for it at all. We guess only that first the growth rate was increasing, then decreasing. But from this moment we start to manipulate this handful of data, which is dangerous. So let us define first, what is the question which we want to answer. It is simply: 6-7 years or 11? So we can manipulate the data until we do not smuggle or remove 6-7 and 11 year periodicities.

            Now consider Fig. 2.2. A 6-7 year periodicity is guessed. So before finding the trend this periodicity is to be suppressed. The easiest way is

              x_tr(t) º (x(t-3)+2x(t)+x(t+3))/4                                                                        (2.6)

The points are seen on Fig. 2.3: the trend is clearly falling linear between 10 and 32. Then what else to do than to try with a rising linear function between 4 and 8 and a constant from 33? A linear trend is the lest arbitrary. Then, making least square fits we get:

              x_tr(t) ~ 1.725t+2.10                            4£t£8

              x_tr(t) ~ -0.6127t+23.30                      10£t£32                                               (2.7)

              x_tr(t) ~ 3.20                                        t>32

That is seen too on Fig. 2.3, and we simply extend the first formula to 9. (Obviously, a least square fit is inadequate for pairwise anticorrelated errors, and App. A shows what else could be done; but the trend seems correct.)

 

 

 

 

 

 

 

 

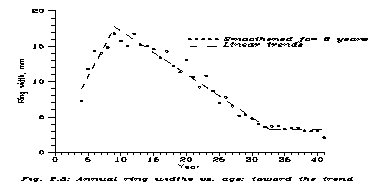
            Have we smuggled in or out periodicities of 6, 7 or 11 years here? No. From this moment we forget about eq. (2.6), only the linear trends remain and they do not inherit the 6 year smoothening.

            Now we have x_tr(t), so we can remove the trend:

              z(t) º x(t)/x_tr(t)                                                                                                (2.8)

That is Fig. 2.4; it nicely fluctuates around 1, so now we can calculate the autocorrelation, going back to eq. (2.2), with x=z(t), y=z(t+t).

 

 

 

 

 

 

 

 

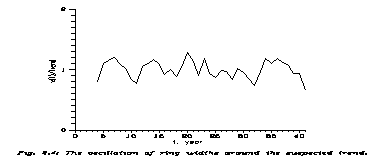
 If there is some periodicity in z(t), r(t) will show it. The 1s level of r is cca. 0.17 for small t's, and 0.2-0.25 between 10 and 20. The r(t) function is displayed on Fig. 2.5.

 

 

 

 

 

 

 

 

 

 

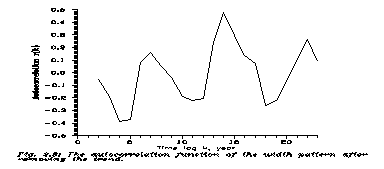
            Now, there are positive peaks at 7 (1s), 14=2*7 (2s) and 22~3*7 (1s); there is a negative peak before 7 and an expressed negative peak at 11. We formulate here 2 hypotheses and try to choose among them. Namely,

            There was something in the lower miocene at the site of the later Ipolytarnóc, influencing the growth of the tree

            A) with cca. 7.2 year periodicity and there was nothing with 11 year periodicity;

            B) with cca. 11 year periodicity and nothing with cca. 7 year periodicity.

            Let us finish first with B). If there was nothing with 7 year periodicity, then the 3 positive peaks are independent random upward fluctuations. Assuming (in the total lack of information) a Gaussian distribution of fluctuations of r, its probability is ~0.025*0.16²~6*10^-4, which is so small that we may forget the possibility.

            So there must be a periodicity with cca. 7 year. Then we understand the negative r(t) before 7; the expressed negative value at 11~1.5*7, and the positive peaks at 2*7 and ~3*7. There is no problem at all with the curve. It is interesting that the first recurrence is higher than the basic periodicity; but it is a commonplace about sunspots that the true sunspot cycle is 2*11 years now (because of the change of magnetic polarity). I do not know how could a tree feel the polarity, but I do not know either how it feels the sunspots.

            Is it possible that 2 periodicities existed, with 7 and 11 years? It is possible, if both correlated positively with the growth, and if the 7 year one was dominant. Then its 3/2 period overcompensated the other into negative, its 2^nd period overcompensated the 3/2 period of the second into positive, and so on. But the second periodicity simply cannot be seen.

            In Ref. 6 we calculated the 7 year Fourier component of z(t), extracted from the function, and then simply there was no autocorrelation at all at 11 years. This I do not repeat here, simply state that no trace of 11 year periodicity is seen. Of course, it is possible that the 7 year periodicity was not the solar activity but something else, and the solar activity did not affect the miserable tree; but if all 11 year periodicities are always attributed to solar activity, then why not this 7 year one?

            So far so good. But from Australian Precambrian layers 11-12 year periodicities are reported [7], and a recent German analysis on Miocene trees claims just an opposite result [8].

            Let us concentrate on Ref. 8, because the Precambrian is very far in the past. In Lower Lusatia two Miocene trunks of Taxodioxylon gypsaceum was found, with 1089 and 1575 rings, not at all evaluable. This is such a large statistics that standard methods can be applied without any problem; and so they have been. The result, according to statements of the Abstract of Ref. 8, is a 12.5 year periodicity "near to the recent length". However in all analyses there is a shorter period too, cca. 5.7 years.

            Now, there are various possibilities. Maybe there is a 6 year periodicity, with the first, and again stronger, recurrence at 12 years. But there is another obvious possibility too.

            The trunks are from miocene, but they seem later than Pinuxylon tarnocziense. The latter is Lower Miocene, and is estimated to be of 23 My old; the Lusatian trunks are estimated to be 15-20 My old [8]. It is possible that Sun changed its internal state between -23 and -15 My. This is an interesting possibility; let us hope that a more vigorous tree will be found from Lower Miocene.

 

3. SUNSPOTS AND ENGLISH PRICES

            It is widespread although seldom quantitative opinion that solar activity (e.g. sunspot number) has some influence on terrestrial meteorological, biological and sociological processes. However the idea is often considered superstitious, and, according to my experience, it is impossible to publish anything about it in journals of natural science or economy. Rightly so; we shall see why.

            Up to now, no sufficiently effective mechanism has been found, able to transfer the effects of solar activity bodily to the bottom of the atmosphere. (Except for special cases: e. g. Ref. 9 could explain one observed correlation. Hudson's Bay Company bought more fox and lynx skins during high activity. Here the explanation is the better illumination on arctic nights of High SRN by the extended polar light.) True, some slight correlation between sunspot numbers and total power output is reported [10], but it is almost impossible to get significant results even on phenomenologic level. The statistical error of the correlation coefficient is ~9% for series of 150 data. Consider e.g. correlation between sunspot number and climate. At the present state of meteorology it is better to use annual averages, and then it means a data base of cca. 150 years at best (the length of regular meteorology records), and in the same time a correlation much higher than 9% would be a miracle. So the task is extremely hard. And, as we shall see, there is a great danger that the result produced by the mathematical analysis is not an effect but an artifact.

            So it is vital to get as long data basis as possible. Now, the maximum for sunspot numbers is a reconstruction back to 1645 AD [11], slightly above 300 data. But solar "constant", annual

+average temperatures, moistures &c. cannot be quantified back to the middle of the 17^th century. Still, there is a quantity aggregating somehow meteorological, biological and sociological phenomena, whose reconstructed values are available from 1661 AD, which is, as we have seen, almost the maximum length to compare with sunspots. Perhaps strangely, this quantity is the price index in England [12].

            Let us see if there is any correlation between sunspot numbers and prices. The idea of such an exotic correlation may seem baseless, but is by no means impossible. Ref. 9 qualitatively mentions anticorrelation between wheat prices and sunspot relative numbers r. If SRN influences the growth rate of trees, it may influence that of wheat as well.

            Here we will not want to decide preliminarily if such an influence exists. Some authors oppose this idea (see e.g. [13]), some others do see the sunspot cycle in recent tree rings [14]. Statistical analyses are just the proper tools to collect more arguments in the debate.

            Ref. 9 mentions lower prices at maxima, not greater. This latest point is supported by some tree ring patterns (greater growth rates at maxima, although Ref. 9 classifies the correlation as "honest-to-God"). It seems that solar activity indeed has a very slight influence on terrestrial climate [15], but let us ignore all the models in this Chapter; they are incomplete at the best case.

            I repeat: as far as annual averages are used, it is impossible to find two series to be correlated longer than 400 years. And, quite independently from the actual mechanism, it would be useful to see if correlation exists between SRN and the price index. E.g. historians and brokers could use such a result, even if its significance is not quite at 3s level (what is at 3s level in history and economics?). So, with all the reservations about reconstructed data, we may proceed. It is possible that reconstructeurs have smuggled a nonexistent 11 year periodicity into SNR in the XVII^th century, but it is not too probable that the economists have done this with the price index.

            For our analysis we use 3 different sets of data. The first is the annual averages of sunspot relative numbers s(t). These data are reconstructions between 1645 and 1826, however based on records of real observations. The second is the annual price index p(t) in England, reconstructed back to 1661 [11]. More efforts are unnecessary because the starting point is the first peaceful year of the Stuart restoration. Between 1642 and 1660 there were the exceptional years of the Cromwellian civil war, and before 1642 even the reconstructed sunspot numbers are not continuous (and we are already very near to the beginning of any telescopic observation in 1609). Finally, the third set, in order to have the long range trends, contains the wheat prices w(t) at the Exeter market averaged for quarters of centuries. Such averages would be available back to 1316 [16]. The details can be found in Ref. 17.

 

 

 

 

 

 

 

 

 

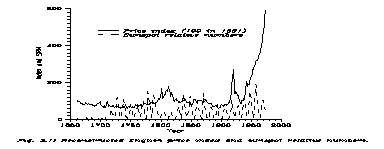
            The curves s(t) and p(t) are displayed on Fig. 3.1, w(t) on Fig. 3.2. In s(t) one first can observe the second part of the famous Maunder minimum until 1715 then a very roughly quasicyclic behaviour of cca. 11 year period begins, superimposed by the cca. 80 year Wolf-Gleissberg cycle. Price index p(t) starts from a rather high point just after the civil war, and then for 270 years (except wartime) remains below the original level. And this is an important fact. People generally believe in these years that inflation was a continuous creeping process; it is not so. Economy must do serious things to get a continuous inflation.

 

 

 

 

 

 

 

 

 

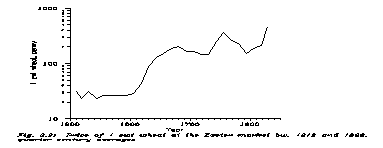
            From 1940 one can see a continuous inflation, triggered by the Second World War, but continuing even in peacetime. The small fluctuations on the curve may or may not be correlated with s(t), but such a correlation, if exists at all, is far from being transparent.

            Now we are going to make a correlation analysis between the SRN and the price index. If there is no significant correlation, then they are independent. If there is, then they interdepend, maybe indirectly. The correlation coefficient was defined in the previous Chapter.

            One can directly evaluate r(t). The results are similar to the folklore: high and obscure correlations. But these results are obviously artifacts.

            Take xºs, yºp. Then one gets curve (a) of Fig. 3.3, and this curve is uninterpretable. Assume e.g. that high s causes high price. Then r(0)>0, but at t=6 yr sunspot minima take the place of maxima and then r(6) must be <0, which is not so. Our guess is that the result comes from the accidental coincidence of the continuous inflation since 1939 and the ascending part of the present Wolf-Gleissberg cycle. In these decades the non-oscillating parts of s(t) and p(t) move together, which indeed leads to R(t)>0. This fact demonstrates how careful one should be with calculated correlations, and how unreliable isolated data from shorter data bases may be.

 

 

 

 

 

 

 

 

 

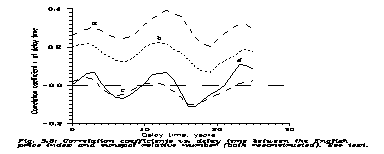
            Note that the absolute value of s measures solar activity, but the absolute value of the currency does not measure anything [18]. So inflation puts a trend into p(t), and then r does not have to oscillate around 0.

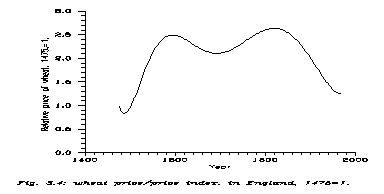
            According to this conjecture the next step is to take out the inflation trend from p(t). The simplest way is to divide with the Exeter wheat prices. This is curve (b) of Fig. 3.3; it is better than curve (a), but still uninterpretable. The reasons can be manifold; for example in England the secular changes of the food prices are not parallel with those of the total price index (see Fig. 3.4).

 

 

 

 

 

 

 

 

            Then one is desperate. Let us simply cut off all data after 1939; then the "secular" inflation is removed. Now Curve (c) is obtained; this curve is quite reasonable globally, having an 11 year quasiperiodicity and going into negative in the valleys. So indeed it seems that the inflationary trends of p caused the first, uninterpretable, correlation coefficient.

            However, in this way we lose 35 years, and, what is even worse, have created a hand-made data series with the possibility of smuggling some tendency into it. But we can as well form rolling averages <p(t)> of p(t) itself to determine the trends, and take xºs, yºp/<p>. Naturally, the investigated quasiperiodicity must not cancel, so it must not remain in <p>. This can be achieved by forming just 11 year rolling averages. Then some data at the beginning and end become lost, but we still can use points between 1667 and 1968. r_sp/<p> is Curve (c); it is fairly symmetric with respect to the axis r=0 and is quasiperiodic with cca. 11 year periodicity. Therefore there is no more evidence to be an artifact, and it may somehow be connected with the oscillation of s(t). The maximal correlation is ~7% at t»2.5 years. For the error eq. (2.3) yields s_r»5%.

            Now one may ask about significance and meaning of the result. For the first question the answer is reasonably definite, but not for the second.

            As we have seen, r²~s_r². Therefore the significance of correlation at any chosen t is poor. However r(t) exhibits a quasiperiodic behaviour as expected for the effect of a quasiperiodic agent. Were SRN(t) sinusoideal, then r(t) should be a cosine, and if it is such indeed, then a period yields 11 points for measuring r. This would decrease s_r by a factor 1/Ö11 » 1/3, thus arriving at 3s significance level, completely sufficient. The present case is not so optimal, since we cannot check the detailed form of r(t) not having a prediction for it. However its general form is good, symmetric, quasiperiodic and the quasiperiodicity lasts at least two periods, t»22 years, so we can regard r_o»7% as checked on a number of points somewhere be­tween 1 and 22. Then s_r should be decreased by a factor between 1 and 1/Ö22. For more definite statement hypotheses would be needed; until that one may obtain a conservative estimate by telling that r has been measured in the 4 extremal points (two minima and two maxima). Then s -> s/Ö4 » 2.5%, i.e. we are almost at 3s level, which would mean that the probability of no correla­tion is lower than 1%. So, our opinion is that the English prices from 1661 show a correlation with sunspot relative numbers whose maximum is (7±2.5)% at 2.5 years delay. (Note that r is a rela­tive date; r»7% does not mean that price changes would contain a component being 7% of the change of sunspot number; instead it means only that 7% of the total short range fluctuation of the price index is parallel to the changes of the sunspot relative number, and Fig. 3.1 shows that even the total fluctuation of p(t) is moderate.)

            Concerning the meaning of this correlation, we do not know anything. But one may guess e.g. to have hard winters just after sunspot maximum. If so, some part of next year harvest is possibly destroyed, causing high prices. And indeed, reconstructed r data show a high maximum in 1787, 2 years before the French Revolution, followed by wheat shortage and high bread prices. So, until no more is known about possible mechanisms, one may try with the indefinite idea that meteorological changes caused by solar activity may drive oscillations inherent in economic systems (such oscillations are indeed known in great abundance), and the delay time takes its explanation from characteristics of the particular economic system.

            The present analysis seems to demonstrate the difficulty of such investigations. First a high and very significant correlation is obtained, but it is an artefact. Then, removing the causes of this impossible kind of correlation, one gets a new, substantially lower, coefficient whose behaviour in itself might quite be reasonable. However, the error cannot be estimated by standard methods, therefore the result of any significance check may or may not be believed. It seems that the correlation is significant just at cca. 3s level, but the statement is between a suggestion and an established fact, and could be made final only by developing special methods for determining the error for this specific correlation mechanism. In addition, no explanation is known for the time lag. It is the reason that one can read extremely diverse statements of the existence, nature and degree of sunspot influence on human life. Still, the results at least sugest that there is something to be clarified.

 

4. ABOUT SPURIOUS SCATTERING

            Spurious scattering is very probably not a scattering at all, but it is obviously of spurious origin. For definition and details of analysis see Ref. 19. Recapitulating only the very essence, consider a track without external magnetic and electric fields (this was just the case in cosmic ray measurements in the 30's, when balloons could not lift up complicated apparatuses). Still the fine details of the track can show the energy of the particle via the evaluation of mean sagitta squares. First the sagittae D_i are defined. The i^th one is built up from the i^th and neighbouring points of the track of coordinates

            (x_i-s,Y_i-1); (x_i,Y_i); (x_i+s,Y_i+1)

where s will be called cell length and then

            D_i≡Y_i+1-2Y_i+Y_i-1                                                                                 (4.1)

Now, <D²(s)> characterizes the winding of the track. It can be shown that the Coulomb scattering leads to [19]

            <D²(s)> ~ cs³                                                                                       (4.2)

where the Coulomb factor c depends on energy and emulsion composition. Calibrating the same emulsion in the laboratory we know c(E). So the task is to determine c's of the tracks in the ballooned emulsion, then the particle energies are known.

            To determine c one must perform a fitting, but then a trial form is needed. The most obvious one is

            <D²(s)> ~ a + cs³                                                                                 (4.3)

where a is the mean error of measuring Y_i. That means a 2-parameter fit, a and c must be determined simultaneously even if nobody is too interested in a.

            However, experimental data do not follow this law. Jánossy rather found a more complicated law

            <D²(s)> ~ a + bs + cs³                                                             (4.4)

with which the agreement was always excellent.

            Let us go again back to the 30's. Nobody was interested in b; it was needed only for the simultaneous fitting. Still a name was needed for the mechanism behind b, and it was called spurious scattering, maybe because it was hard to find the real mechanism behind. Ref. 19 gives an explanation: this term appears if (maybe during the treatment) the emulsion disintegrates into mosaic-like parts and they slip in random directions. In Jánossy's measurements b~10^-4 µm, which is conform to 0.1-1 µm individual slips at 100-1000 µm intervals.

            So far so good. Emulsions in the developing fluid may soften and disintegrate slightly, and then cosmic physicists have measured the extent of disintegrations, slips, rotations &c., which is good to know but not too fascinating. Later this specific balloon technique faded out, and the mechanism behind b did not interest anybody except L. Jánossy from 1971.

            Then he restarted to invent a theory beyond standard Quantum Mechanics, in which wave packets underwent repeated reductions spontaneously. For the details see [20]; the theories are irrelevant here, only the fact that it would be very important to see something beyond standard QM. E.g. unification of gravity and QM could result in repeated reductions, winding paths, anomalous Brownian motions, &c. [21], [22], [23]. Jánossy would have preferred if the wave functions of elementary particles had remained always microscopic, and recognised that spurious scattering could be explained via repeated reductions.

            Jánossy suggested to start an extended measurement to see if b is really significantly nonzero, energy-dependent, particle-dependent, and so on. He asked his Serpukhov colleagues to shoot a monoenergetic proton beam of 70 Gev on emulsions, and got a single emulsion from the first calibration runs of the Batavia accelerator, still at 200 GeV. Monoenergetic tracks can be added up, and so the statistics is excellent. In that time tracks were measured by scanning girls of half-time jobs, and human labour was cheap in Hungary, so it seemed that nothing could prevent full success.

            But sometimes Fate is merciless, and in this case many malevolent factors added up to hinder the project. Jánossy was at that time at the Academy of Sciences, not at CRIP, so the suggestion went through several levels of hierarchy. At the end the particular experimenter performing the task was not informed about the theory. Still that was not fatal. But in addition this experimenter was female and married during the measurement. Therefore after some time she stopped for a while to produce babies, and when she returned, Jánossy prematurely died in a heart attack. Then she had the data, but not the theory, and could not write an article. The data were stored, specially on holed paper ribbons read by special Bulgarian machines.

            This was so until I heard about the story in 1990. I knew the theory. So after 15 years again theory could meet data. But could they? We started to look for the data (on the holed paper ribbons) found some ribbons but not the Bulgarian machines reading them. There was a rumour that in an indeterminate time between 1978 and 1990 the data were copied to a magnetic tape, but that tape was not in use either anymore. And so on. After a quarter year a fragment of data were found in a notebook. That data, with some scattered cosmic physics publications from the 60's, are the total available databank of spurious scattering.

            And there is very little hope to make new measurements. The original balloon technique is out of use. Particle physical measurements do not use too much photoemulsions either, and the other techniques cannot go down to 1 µm precision. Scanning girls are rare and expensive. So until a very rich Quantum Gravity project is not convinced to support new measurements, the phenomenon is practically not repeatable, although it belongs to standard experimental physics, where everything is repeatable.

            And now some results. For the details see [20]. We evaluated measurements at 4 energies: 0.25 GeV, 9 GeV (both published, with moderate statistics, in the 60's), 70 GeV (the Serpukhov tracks) and 200 GeV (the Batavia tracks), both measured between 1972 and 1975. Unfortunately, the 4 emulsions were all different.

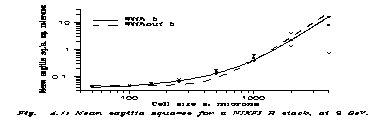
            At 0.25 GeV E. Fenyves and Éva Gombosi measured one track [19] whose energy was determined from parameter c in the spirit told at the beginning of this Chapter. The spurious scattering parameter has been calculated recently by us from the published sagitta squares. There were 37 measured sagittae N=37 at s=500 µm. The 9 GeV data can be find also in Ref. 19, but in a different form. There <D²(s)> is given at 8 different s values (that is Fig. 4.1) and thence a, b and c can be calculated by a least squares fit. (For that the b term is indeed necessary.) The source does not give N, but even then the error can be calculated from the fit. The emulsion was a NIKFI R stack.

 

 

 

 

 

 

 

 

 

 

            The measurements at 70 and 200 GeVs, were performed visually and manually by two microscopes of the same type KORITSKA. The last readable digit was 0.1 µm; however the reliability seemed to be rather 0.5 µm if returning later to the particular point. It is worthwhile to mention that the majority of the 70 GeV Soviet plates was slightly bent, and the thickness of the emulsion had also some gradient. This hindered the measurement, and reduced the number of appropriate tracks by cca. 40%. The elementary cell size was 0.5 mm, and the number of processed sagittae was cca. 3000 at 70 GeV, and cca. 2000 at 200 GeV. The mathematical method of the analysis was the same as given in Ref. 19. Here we only mention that the global curvature of tracks (and plates, if so) were removed by a fit of prescribed way via 2^nd order Legendre polynomials. The final results of the analysis are given in Columns 3 and 4 of Table 1.

            In addition, at 200 GeV the mean sagitta squares were measured at 4 other s values too, namely at 1, 2, 4 and 8 mm's, obviously with less statistics. This, in principle, enables us to determine the parameters in an alternative way too (the one followed at 9 GeV). This would be dangerous, having only 5 points to determine 3 parameters, but is somehow still a check.

            The results are

 

E, GeV	0.25	9	70	200
a, µm2	-4.97*10-2	3.33*10-2	2.94*10-1	-4.47*10-3
b, µm	1.31*10-4	1.33*10-4	2.16*10-5	1.02*10-4
c, µm-1	2.54*10-10	2.41*10-10	1.12*10-10	2.92*10-11
saa, µm4	3.60*10-3	1.37*10-5	1.17*10-4	2.78*10-5
sab, µm3	-3.96*10-6	-1.09*10-7	-6.71*10-8	-2.39*10-8
sac, µm	2.79*10-12	7.87*10-14	2.40*10-14	3.99*10-15
sbb, µm2	4.75*10-9	1.21*10-9	5.48*10-11	2.50*10-11
sbc, µm0	-3.66*10-15	-9.95*10-16	-2.27*10-17	-4.51*10-18
scc, µm2	8.29*10-21	4.97*10-21	2.40*10-23	4.38*10-24
N	37	?	~ 3000	1885

 

The parameters of eq. (4.4) and their error matrix from the mean sagitta squares

 

            Now: what have we learnt? First, one can compare b to Ös^bb . Then b differs from 0 on (cca.) 2s level at 0.25 GeV, on 3s at 9 and 70 GeVs and on 20s at 200 GeV. So spurious scattering does exist, and this was possible to prove even at the moderate and practically unrepeatable database. Then let us look at the values and energy dependence of b (Fig. 4.2). The result is disturbing, because of the deep depression at 70 GeV, which is strange in the best case. That smaller b belongs to the inhomogeneous and bent Soviet plates, and how can distortion make b decrease? We have seen that disintegrations & slips or rotations mimic the effect, not obliterate.

 

 

 

 

 

 

 

 

 

 

 

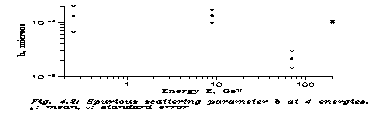
            We have no serious answer (the measurement is not repeatable now.) So let us turn to the error matrices. The Table  shows that da and db are very strongly correlated at any energy. Since correlations with dc is not so substantial, one can visualize the situation in a 2 dimensional parameter subspace (a,b). Then it is characteristic to have a "diagonal" error ellipse, but it is also striking to have negative a values (i.e. background noise) at some energies. From these two facts it is clear that some part of b must be an artefact, and should be considered as belonging to a. One might, e.g., argue as follows. The width of the track is cca. 1 µm. If its center is not correctly found, there is 0.5 µm random walk in each 500 µm step. However, consider the following facts. First, we used two very different ways of analysing the data; in one of them the step length varied between 50 and 4000 µm's and still the linearity remained in the final results. Both methods gave b values roughly similar (except for 70 GeV) and quite significantly nonzero; and both methods gave strong correlation between da and db. So the b values cannot be simply false consequences of systematic errors of a particular method. Second, even with this strong correlation the error ellipses are far from the b=0 axis. Therefore the systematic errors are quite possible, nevertheless spurious scattering seems to exist and the order of magnitude of b is 10^-4 µm.

            One then may ask what is what we see? Ref. [20] lists very various possibilities. Without going into details I recapitulate them as follows.

            The conventional explanation is mosaic-like disintegration and minute slips in the emulsion. Then the spurious scattering parameter would depend on the type of emulsion and on the details of treatment, while would be fairly independent of the particle and its energy. However in the present measurement the parameter b does not seem to depend either on energy or on the actual type of emulsion (except for both possibilities the strange 70 GeV case, which was just the case when the emulsion was in the worst shape, so it would be hard to imagine that disintegrations and slips would have been minimal there). This explanation, then, does not seem too probable.

            The alternative possibility is that a "quantum stochastic" effect of any kind is seen. There are various suggestions for such mechanisms; let us try to compare the results with the (rather qualitative) predictions of different reduction models. Let us note that <D²(s)>_~bs is a kind of "anomalous Brownian motion"; it is a random walk term.

Self-interaction.

            One can put nonlinearities into the Schrödinger equation. Such term may stop the spontaneous spread of the wave function, but in itself does not lead to reduction, so does not lead to anomalous Brownian motion either. See e.g. Ref. 24.

Repeated quantum stochastic multiplication.

            This is the mechanism suggested by Ghirardi, Rimini and Weber (see [25]). The mechanism is a free expansion for time t and then multiplication by a Gaussian of width s. One would think that by choosing the new parameters of that theory to s~10^-4 cm and t~10^-12 s, to get the observed random walk. However, in this mechanism the above parameter values do not lead to 1 µm random walk in each 100 µm's. During the prehistory of the proton, a large number of such cycles has happened, therefore now, when passing the emulsion, the cycles must be stationary, i.e. all cycles must start with the same width. Ref. 25 gives the evolution of a Gaussian wave packet through cycles. Introduce the dimensionless parameter e as

            e º th/ms² ~ 10^-9 << 1                                                                                    (4.5)

Then, substituting into the formulae of Ref. 25 one gets that in the stationary case

            <(q-<q>)²> ~ Öe s²

            <(p-<p>)²> ~ h²/2s²Öe                                                                                    (4.6)

            <(q-<q>)(p-<p>)> ~ h/2

            Then a simple but tedious calculation gives the random walk obtained from jumps located in the region Ö<(q-<q>)²> , with the result

            <D²(s)> ~ 4(h/p)s + (1/2s²)(h/p)²s²                                                                  (4.7)

where p is the original momentum in x direction. So both a linear and a quadratic spurious scattering is obtained. However the amplitude is too small. With the above s~10^-4 cm for a 70 GeV proton at s=100 µm the sagitta square is cca. 10^-17 cm², 8 orders of magnitude below the experimental value.

Influence of stochastic background.

            Something stochastic and fundamental, in the background of other theories, is disturbing the wave packet. If that background is stochastic gravity then no observable spurious scattering appears. Namely, elementary particle masses are so low that gravity breaks down the superposition only in astronomical times. (A rough estimation based on Refs. [22], [23] gives 10⁵³ s.) If the background is a so far unknown stochastic field, any result can be obtained, of course.

Berkeleian omniobservant reduction

            After discovering QM Bishop Berkeley's slogan Esse est percipi [26] might have been partially reinterpreted, at least in the orthodox QM because perception is a kind of Measurement. So his viewpoint would mean that objects not measured by us are measured time by time by God or Nature.

            What is percipio? According to orthodox QM, percipio~metior, pondero. If so, in our age the Bishop would say that a body not measured by any of us is still measured by God, and therefore His omniobservancy keeps the states only microscopically smeared. The idea is similar to the repeated quantum stochastic multiplication, but not at all the same. We have just seen that if there is no enough time between multiplications, then the wave fuction is continuously shrinking and after some time drops below even the well checked atomic sizes. In contrast, repeated Measurements only restore again and again some limiting size. The simplest example is as follows. Assume that the system has its own linear Hamiltonian, but there is another, Divine, Hamiltonian as well, giving too high energies above a limiting size S1 µm, and God applies it on all wave functions at t intervals. Then for a bound microscopical system practically nothing happens, because below S the effect of the Divine operator is negligible. For an unbound particle nothing happens until the expanding size is below S. When the size enters that range, however, then each Divine Measurement substitutes the wave function with one of width S centered somewhere in the region where before Measurement it still was substantial. Then further expansion stops, and there appears a "random walk" with S steps at t intervals.

            However no definite model exists up to now. So we can only say that the measured spurious scattering data may be compatible with a repeated Divine Reduction. Numerical calculation is unnecessary here; [19] gave the formulae for a random walk, which remain valid, mutatis mutandis, when the random walk is caused by a Measurement independent of us, say, with a limiting width S~0.1 µm, and with a repetition time t~10^-12 s. Then b~10^-4 µm, as measured. However now is the proper time to note that electron and neutron splitting experiments above µm range strongly oppose such an explanation, and, in addition, theology is not the proper explanation for a single, unrepeatable measurement.

            There remains a possibility. It is not yet ruled out that the observed effect is a quantum stochastic one, but not at the particle but in the emulsion. Namely, in an emulsion there are silver-halogenide grains of the size of µ~1 µm. Now, the situation is too involved for detailed calculations, but consider dimensional analysis. In a nonrelativistic (Newtonian) Quantum Gravity there are two fundamental constants, G and h. Consider now characteristic masses m in the matter; then the only possibility to get a characteristic length is

              b ~ h²m³/G                                                                                                     (4.8)

Then a b~10^-8 cm can be (somehow) obtained from masses ~10^-13 g, which would be ~3*10^-5 cm grains in the emulsion. For more details see [27]; such grains are there, we cannot calculate the effect in more details, since it would need the unification of Quantum Gravity and materials science, which needs time. In addition, as we know, the measurement cannot be repeated just now.

            Here, therefore, we may and should stop. But: spurious scattering exists. That is a result.

 

5. ON THE CHRONOLOGY OF WORLD'S FIRST KINGS

            Proper history starts with writing, because illiteral nations could not transfer names of persons, sites &c. to posteriority. In addition writing appears with the beginning of state organisation. So historians have a good chance to decipher the names of the first kings; and, if some more detailed texts survived, then their correct chronology can be restored too.

            Two areas may have the claim to have brought the first states into life: Egypt and Sumer. Egypt was unified by Menes roughly at 2900 BC, and before small statelets existed along the Nile; Sumerian city-states predate this time by some centuries. In Hellenistic ages Manethon compiled an Egyptian history back to Menes, maybe from original sources, but from Sumer we do have the original sources. Or almost so: the available copies of the Sumerian King List [28] come directly from the XVIII^th century BC. It seems that the original was compiled in cca. 2120 BC, in the upheaval of Sumerian national feelings when King Utuhegal of Uruk liberated the Sumerian cities from the Guti overlordship.

            Unfortunately the Sumerian King List starts strangely [28]. It tells that when the institution of kingship descended from Heaven, then the first royal capital was Eridu. That is quite possible, since Eridu seems to have been a very old city in the marshes. The name of the first king is given as Alulim, but his years of rule as 28800 years, which is rather strange. After 8 kings, 241200 years total, the Flood swept over the cities and kings. Although this age is in fair accordance with the age of the "mitochondrial Eve" of human geneticians, serious caution is needed.

            Now, Prediluvial kings may be mythical. After some time, says the List, kingship again descended from the Heaven, to the city of Kish. That is possible, Kish was a powerful city of the north, on higher grounds, so less damaged by the Flood (anything was that). The king is named Ga...ur, the middle syllable illegible already for the scribe 3800 years ago; but the length of rule is 1200 years. The Kish I dynasty is 23 kings altogether, and the summed time is told to be 24510 years, 3 months, 3½ days. This time could be good for the appearance of Homo sapiens sapiens at the spot, but not for kings of Kish.

            There are logically possible solutions. E.g.

              A) the first kings might have been demigods;

              B) the time data may have been completely fictitious;

              C) the kings may have been fictitious too;

              D) some changes of the calendar are reflected; and so on.

            Explanation A) is ignored here on the ground of physicists' common sense (for any case no dishonour is meant for the shadows of the first Sumerian kings), case B) is quite possible, but then we throw away all the data, case C) is disproved, because King Enmebaragesi, the 22^nd, who appears on the List with 900 years occurs on an alabaster vase, ritual gift to the Nippur shrine [29].

            Case D) represents a whole class where some transformations, deliberate or accidental, happened on the data. In addition, a part of the data may be sheer guess. Now, can we do anything with the data? There is no parallel source; it seems that at the beginning of Kish I Egypt still consisted of statelets, without registering Mesopotamian history.

            In addition, the List is incorrect in one more sense. It puts all the known rulers (except those of Lagash, who were ignored as traitors, tax-collectors and puppets of the Guti just before collecting the list) in one continuous line, always a sole ruler for Sumer. But that is clearly not so: tradition mentions rulers of the List warring with each other, e.g. Gilgamesh of Kullab, the son of a lillu demon, King of Uruk, with Agga, son of Enmebaragesi, of Kish. Can anybody do anything with such a list?

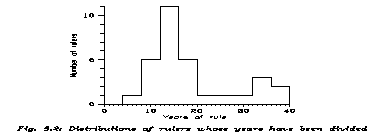
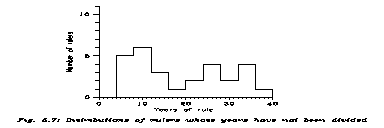
            Only if not utter and final certainty is pursued. But that is not necessary. Radiocarbon dates exist for cities, hence the greater rulers can be dated with 1-2 centuries of error. If a method gives less error with some acceptable probability, then we have learnt something. This plan was executed in 1975 [30], but in the next 24 years the statistical analysis improved slightly. For the details, numbers, references &c. see Ref. 30; here I give the essence, and some considerations absent in Ref. 30.

            Now let us see some raw data. The ruling times here are denoted by t, calendar time by t. We consider 66 rulers, namely all whose data are legible from Kish I, II, III & IV, Uruk I, II, III & V (Uruk IV being very special, as puppet kings), Ur I & III (in Ur II all numbers are illegible), and Agade (except for 4 successive kings ruling 3 years altogether). Now, a lot of too large numbers are divisible by 60, and the Sumerian number system was based on 60. (The time of the introduction of strictly sexagesimal system is not clear, but for mathematical and astronomical texts it was general about 1900 BC.) At sexagesimal positions, however, decimal numbers were used, vertical wedge for 1 and horizontal one for 10. Zero was not used until very late and only in astronomy. For more details see App. B. So, e.g., 10, 60, and 6=60/10 may appear in misinterpretations, misticisation &c. E.g. doubts about a factor 60 can be visualized even by arabic numerals.

            In sexagesimal system our number 721 is written as

12;1

i.e. 12 "large units" (one vertical and two horizontal wedges) and one "small unit". Indeed 12*60+1=721 in our system. But

12

is awkward, it may be 12, 720, &c. A scribe may have been surprised to find 12 years for an ancient divine ruler, and may have been tempted to correct 12*1 to 12*60+0*1. This is not a proof, only a possibility.

            Now let us try with a desperate guess. We do not accept numbers above 59 years, but if they are divisible with 60, 10 or 6, we try to assume that they have been multiplied with the actual factor. Sometimes this method is not unique; then we require that the result of the division be, say, between 8 and 59.

            Then the 66 numbers behave as follows. 30 do not need manipulation. 3 should be divided by 6, 11 by 10, 18 by 60, and 4 are completely uninterpretable in this way

            Now, the reader may tell that artificial numbers can be produced by dividing impossible numbers with artificial ones; and that is true. However we will immediately check this working hypothesis.

            In the 4 groups there are 4 distributions. We cannot check if the distributions are similar but scaling, as expected for multiplicating factors, because one group contains only 3 kings. However we can compare the averages.

            This is done by a 2-parameter fit:

              <ln t>_i » ln a + kln c_i                                                                                      (5.1)

where _i stands for the groups 1, 6, 10 and 60, and c_i are ln 1, ln 6, ln 10 and ln 60, respectively. For this fit we need <ln t>_i and its statistical error. By evaluating the empirical first and second moments in the groups in the standard way one gets

 

	Group	1	6	10	60
	<ln t>	2.873	4.904	5.381	6.835
	s<lnt>	0.120	0.488	0.195	0.058

 

and then we have the weights for the fit (5.1). The best fit is

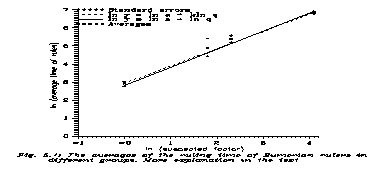
a=18.6 ys, k=0.959

This exponent is almost 1. To check, if k=1 is possible or not, let us make a 1-parameter fit with k=1, then a=16.3 ys, and in the chi² test

              chi²(4-1=3) = 3.8                                                                                                       (5.2)

This means that k=1 is possible on a quite fair level. The averages are statistically undistinguishable. The situation is displayed on Fig. (5.1).

 

 

 

 

 

 

 

 

 

 

 

            So the assumption that too large numbers are multiplied is not disproven. The support would be rather weak in physics or astronomy, but we have no more kings, the statistics is very poor.

            Now let us proceed. One may divide by the suspected factors, and then a distribution is obtained. We have seen that the average is reasonable; let us see if the distribution is impossible or not. All the details are again in [30]. Here we give only the distribution of the times which have really been divided: that is Fig. 5.2. The statistics is even poorer, but the form is not impossible. Its first peak is very roughly Gaussian with

<t> = 15±1 ys; s_t = 5±1 ys

Now, are these parameters possible, or not?

 

 

 

 

 

 

 

 

            For this we need theoretical and empirical considerations. Available theory is very poor. Consider an ideal case when all successions are legal and always the first son succeeds. Then

              t_I = l_I - (l_I-1 - b_I-1)                                                                                            (5.3)

where l is the lifetime, b is the age when the first son is born. Both quantities had some distributions at 3000 BC, of which we know nothing. However if a triple convolution is enough to use the Theorem of Central Limiting Distribution, then f(t) is Gaussian. A triple convolution is not enough; but even then f(t) is nearer to Gaussian than f(l).

            From the convolution

              <t> = <b>

              s²_t = 2s²_l + s²_b                                                                                             (5.4)

Now, for a southern, polygamistic, mainly pastoral civilisation 5000 ys ago 15±1 ys was quite possible for <b>. The problem is rather with s_t; the numbers would permit maximally 4 ys for the mean deviation of the lifetimes in royal families, which is a rather too sharp distribution. Larger mean deviation is expected.

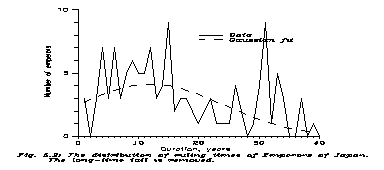
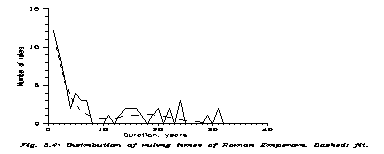
            Now comes the empirical approach. What kinds of distributions can we see for royal rules? Obviously distributions of different societies cannot be summed up, so I choose here 2 very long Imperia, Japan and Rome. In Rome (according to one count of several) there was 118 Emperors from Augustus to Justinian (after whom the society changed), and the present Japanese Emperor is the 125^th one. For the data see [31].

            The Japanese dynasty is sacred, it is claimed that all successions were legal. The distribution is Fig. 5.3: it is roughly Gaussian around 13(!) ys, the distribution is wide. Among the Roman Emperors (Fig. 5.4) many were usurping generals, so an exponential decay law appears at short times (see App. C), and then a small Gaussian peak around 18 ys. The ratio of rulers belonging to the Gaussian is some 21%, a minority. Maybe the Gaussians are the lawful successors and the exponentials are the generals; the numbers are acceptable. The decay time is cca. 3 ys, the Gaussian average is 16.5 ys with 5.6 ys width, quite close to the early Sumerian data.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

            Now let us go to eq. (5.3), because I used it to suggest a Gaussian. Eq. (5.3) leads to an antiautocorrelation between neighbours in the series {t_i}. (A son hardly survives his father of extremely long life.) This antiautocorrelation we cannot check on the Sumerian data because some illegible numbers interrupt here and there the series. So let us see Japanese (Fig. 5.5) and Roman (Fig. 5.6) autocorrelations.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

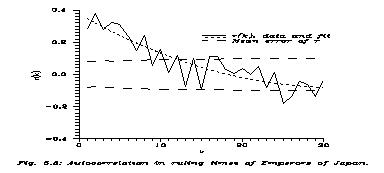
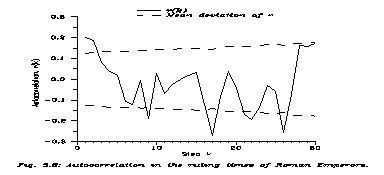
            None of them show anticorrelation between neighbours. The Japanese data are surprising: positive autocorrelations decreasing but existing even for far successors. The Roman data are simpler: positive and significant autocorrelations for close neighbours and then nothing significant.

            The Roman case is simple. Newer and newer dynasties followed, so long-range correlation is impossible. Maybe the mechanism of eq. (5.3) works, however it cannot be seen. Namely, there are two possibilities. A and B are either from the same dynasty, or not. If they are, then the father's ruling time affects the son's, and that is a fluctuation around 16.5 ys. If no, then there is no correlation. Now, the fluctuation has two centres: 16.5 ys ("lawful successors") and 3 ys ("generals"). Compared to this difference the opposite fluctuation between father and son is smaller. Being in the same dynasty establishes more correlation (all being around 16.5 ys) than anticorrelation (due to eq. (5.3)).

            As for the Japanese Emperors, in some times they used a practice, almost unknown in Europe: the insei. The Japanese Emperor is too sacred to be able to govern effectively. The original solution was to nominate brothers, nephews &c. as prime ministers. So appeared the great Fujiwara clan. When it was too powerful, Emperor Sirakawa declined from the throne in 1086 AD, and became a joko ("retired emperor"), helping his son. Now this practice was repeated many times. So for many emperors the length of rule was not determined by the length of life, but rather by a custom, when to retire. That establishes a strong positive correlation.

            Then one can tell that Fig. 5.2 is possible, if most of the early Sumerian kings were lawful successors, not usurpers (no starting exponential is seen, as on the Roman spectrum). The rulers of too long t's are generally the early ones, and one may assume that then kingship was more sacred than later. (Many early rulers have in their names the word "en", meaning "ruler" with a religious accent. Later many kings are called "lugal", which is simply "big man".) Our last check is Fig. 5.7: It is the spectrum of Sumerian rulers who did not need dividing (they are generally from later times). The exponential beginning appears for them. Summarizing, neither <t>, nor s_t is without parallel.

 

 

 

 

 

 

 

 

 

            Then let us accept the divided numbers, let us do something with the 4 numbers which cannot be divided even with 6 or 10. Then we have numbers; where numbers are illegible, let us substitute some averages. All the details can be find in [30]. We need a starting point, and going backwards, all previous kings get their calendar years for the beginning of their rules. For the starting point we need a king who ruled Kish, Uruk and Ur together. The first king, for whom this is sure from almost the beginning, is Sargon, the Conqueror (Sharrukin I of Agade). His rule started somewhere about 2350 BC. Let us accept now this number; if it changes, all other data move rigidly with it.

            The reconstructed data carry uncertainties. The division method is not unambiguous. Some rulers may be missed. At the changes of dynasties some years of civil wars may have gone on. So let us put ±10 ys error for all data got by division, and the same for all new dynasties, but these errors are uncorrelated. Then, in first approximation, all kings have calendar years and mean errors. Now, and only now, can we make historical checks.

            Sumerian texts mention some synchronisms between rulers of different dynasties (e.g. warring with each other). We can directly use only two of them here: the synchronisms of Gilgamesh of Uruk (2637-2616±25) and Agga of Kish (2657-2647±40) [32] and that of Enshakushanna of Uruk (2476-2466±20) and Enbi-Eshtar of Kish (2490-2461±21) [33]. As seen, the synchronism is established in the second case, and is within one standard error in the first.

            Therefore the scarce internal data do not contradict the reconstructed calendar years. The detailed chronological table can be found in [30]; here we give only the founding years of some old dynasties; all BC

 

	Ur II	2466±15
	Ur I	2643±25
	Uruk III	2350±10
	Uruk II	2476±20
	Uruk I	2763±35
	Kish IV	2415±15
	Kish III	2425±20
	Kish II	2647±35
	Kish I	3015±60

 

Since the beginning of the early dynastic period of Sumer is put generally to cca. 3000 BC [34], there cannot be too much problems with these reconstructed data. On the other hand, except for early Kish I, the mean deviations are smaller than in the best radiocarbon laboratories (and how to date a king by radiocarbon whose bones are not available?).

            Now, Kish I started after the Flood. So, the Flood of the Sumerian King List happened at 3015±60 BC. Is it the Flood of the Bible? I do not know. From the biblical texts Martin Luther calculated 2305±? [35], which is already the time of the well known Agadean dynasty, so impossible.

 

6. THE SECRET OF THE FIRST CHINESE VERSES

            F. Tőkei, an outstanding Hungarian sinologist, in his youth formulated an idea about the structure and pattern of the oldest known Chinese verses. He published it with some arguments in 2 papers [36], [37], but, as he said later, in the introduction of a book of his [38], "the scientific literature just acknowledged the papers, did not utilize or disprove them". So, he continued, the author became bored, put away the problem; maybe linguistic methods would be needed to continue. Here I show that statistics will do as well, and make one step forward, just for demonstration. This is a preliminary report; together with I. Borbély we are planning to perform a more elaborate study, but never have the necessary time.

            The question is: what pattern makes an old Chinese text verse? From classical times we know theoretical works, which clarify this problem: then the necessary conditions were: rhyme and a regular pattern of musical tones (which latter is an important property of words in the Chinese language). However, there are more ancient texts in the collection Shi Jing, which were considered always verses (otherwise they would have not been in that collection) but do not show the above pattern. So it seems that in archaic times (roughly until the beginning of Chou era) another rules were valid for verses.

            Unfortunately, Chinese writing is ideogrammatic, so does not reflect the changes of pronunciation. However B. Karlgren reconstructed the archaic forms of many words [39]. Then Tőkei able to formulate his hypothesis. Namely, that the main pattern in an archaic Chinese verse is a regular pattern for the voiced/unvoiced first consonants of words.

            This idea is so foreign from European literary ideas that some explanation is needed. Chinese sources stated that this voiced/unvoiced opposition corresponded to "low/high" musical tones in ancient Chinese (say, the Han era). That is indeed possible, if we define carefully, what is low and high.

            A human sound of speech is a complex superposition of waves, which cannot be represented by a single frequency. However it can be more or less represented by a restricted number of frequencies. E.g. in English and Hungarian it seems that vowels are quite well determined by the first two local maxima of the Fourier spectrum.

            We are interested in consonants, but vowels are simpler so let us see first on them, what may be low and high. In English literature low/high means the position of the tongue at formation, and looking at the frequency plots [40] one sees that for high vowels the first formant frequency is lower than for low ones. On the other hand, there is a back/front opposition, and for front vowels the second formant frequency is higher than for back ones. In Hungarian terminology closed/open stands for the English high/low, and high/low for the English front/back. "Open" vowels have higher first formant frequencies, "high" ones have higher second ones [41]. Hence one can see that terminologies are language-dependent, and we cannot be sure what was meant when a Han Chinese linguist used the term "high".

            However voiced/unvoiced opposition (when exists in a language) is physiologic. Ref. 42 gives the results of successful Hungarian CV syllable syntheses. It seems that many voiced consonants can be characterised by 3 or 4 formant frequencies (moderately dependent on the next vowel), while unvoiced consonants are characterised by noise bands. Now let us see some examples. For [b] F1 is 300 Hz, F2 is around 1000 Hz and F3 is 2300 Hz. For its unvoiced counterpart [p] there is a continuous noise band in the range 400-5000 Hz. For [d] F1 is 400 Hz, F2 is around 1600 Hz, and F3 is 2600 Hz; [t] is a noise band with two maxima at 1600 and 3500 Hz. And so on. Generally, the frequency spectrum starts and ends higher for  unvoiced consonants than for the voiced counterparts. So indeed, voiced/unvoiced can be low/high musically, and if it was so in Han Chinese, it was so in Shang-Yin or Zhou Chinese so.

            Now let us see the patterns. Tőkei notes that one may ignore rhyme, because some ancient verses of Shi Jing, namely N°'s 273, 277, 285, 293, 295, 296, are rhymeless (for the Shi Jing, see [43]). Then he took Verse 8 from the Shi Jing.

            It is a short verse, 3 stanzas, each of 4 lines, each line contains 4 words. The content is rather simple: the actors are gathering some herbs while chanting that they are gathering the herbs. It is rhymed, but let us ignore that. Let us represent here the voiced/unvoiced opposition as 0/1, and then the pattern reconstructed by Tőkei is

 

1 1 0 0

0 0 1 1

1 1 0 0

0 0 0 1

 

This is one stanza, but the 3 ones are identical for pattern.

            It seems, indeed, "regular", but human mind likes to find pattern everywhere, so can we be sure that the pattern is not accidental? Longer texts exist, but they are not such simple. How to be sure that the regularities exist in reality?

            Now, my point is that the investigation can be continued from the data of Refs. 36 & 37, without any further linguistic work. Namely, there are statistical methods to decide if a series is random, or not. If it is significantly non-random, then somebody has put a pattern in it. So (for long enough texts) one can decide if they are patterned for voiced/unvoiced first consonants; if verses are, proses are not and this pattern is the only recognisable pattern, then the question is settled (until another sinologist does not suggest another pattern).

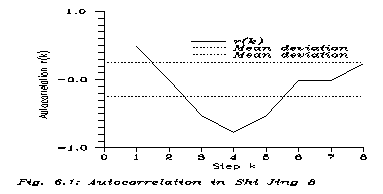
            As told above, this is a preliminary report, so I take only the above Shi Jing 8, mere 16 words. But for analysis a Born-Kármán boundary condition will be used, i.e. I restart the text at the end. This is not the ARIMA trick here: there are 3 identical stanzas, and the text is clearly good for circular singing.

            So regard the text as a linear, repeated, infinite series of numbers 0 and 1. In a random series there is no significant autocorrelation, in a patterned series the autocorrelation is significant. The autocorrelation function is Fig. 6.1; being the elementary cell of length 16, s_r=0.25 in the null hypothesis, when the series is believed to be random. The independent points of r_k are at 1£k£8 (beyond k=8 it has a mirror-symmetric second half), and r_k differs from 0 at cca. 2s level at k=1, 3 and 5 and at more than 3s level at k=4. The chance that all these r values are simultaneously accidental, is much below 0.0001. The text is patterned without doubt.

 

 

 

 

 

 

 

 

 

 

            Now, such an autocorrelation analysis should be done on longer and more sophisticated verses, and, for comparison, proses. Many texts are available without further works, because in Refs. 36 and 37 Tőkei reconstructed the archaic voiced/unvoiced pattern. But just now I wanted only to demonstrate that the hypothesis of voiced/unvoiced pattern can be checked on the data available.

 

7. CONCLUSIONS

            I have shown several situations when statistics was applied at the borderline of possibility (stricter persons would tell that beyond that borderline), and still, with some hand-made and special methods, some result has been got. What is the morale in this?

            First: if one makes some efforts, he gets more result than without it. Yes; but how much worth is that result?

            That depends. Some results are quite reliable, while some others are similar to minors' testifications in canonisation processes (where they only point towards the final result as a small stick and they are not to support us as a cane.)

            For the Lower Miocene ring pattern, I am sure that no 7 year component was smuggled in and no 11 year one out of the data; other distortions may have happened because the determination of the trend was rather handmade. Still, the 7 year component is there at the end, significantly. Of course, it would be difficult to prove that it was the solar cycle and not some up to now unknown cycle of Miocene meteorology. I do not think that this only, isolated sample proves the cyclic solar model. However the result helps in choosing the suspected time when Sun switched at the present way of life. Namely at the Lower Miocene, cca. 23 My ago the solar cycle time seems to have been different from the present one, while slightly later, 15 My ago it was already similar, according to the Lusatian samples. Then maybe more Lower Miocene and Upper Oligocene samples should be investigated (if they exist now). The result is very interesting, but nothing practical depends on it.

            For the connection of the English prices and sunspot relative numbers, I think, I have proven a slight connection. But it is indeed slight. The result simply indicates that slightly higher inflations are expected just under sunspot maximum. In addition I emphasize that the analysis happened only for England: countries of different meteorology may behave themselves differently. The result indicates that there is something to be investigated; but a result between 2s and 3s level is insufficient for final proof. Still, it is an indication.

            For the spurious scattering the statistics is excellent even on the present measurements. The existence of the effect is estab­lished. The deep depression at 70 GeV on Fig. 4.2 shows that mea­surements should have been performed on different emulsions at the same energy; but it was impossible. The result does not prove or indicate Quantum Gravity origin; simply permits it, and there is no harm in that. If one can derive the effect from Quantum Gravity, good; if not, still nobody will throw away a Quantum Gravity theory explaining everything but spurious scattering. Anyway: what if the spurious scattering is the mosaic-like splits and translations and rotations of the emulsion?

            For early Sumerian kings, we have got some rational data from fairy tales. However note that applying the conservative method (say, giving 15 years for each king on the List and 25 to the famous ones) the bulk results, i.e. the beginnings of dynasties, would have been rather similar. Still, this is the result which has utilized the maximum amount of numerical data available. And it is comfortable to know the date of the Flood (anything have been it). In addition, famous Gilgamesh is dated. So everybody is kindly asked not to call predynastic Egyptian finds as an Eastern-type knife at Gebel-el-Arak, or a ceiling painting at the 10^th Hierakonpolis grave, with a bearded man fighting two lions, Gilgamesh-type ones (which did happen [34]). He did not yet live when Menes founded the First Dynasty of Egypt.

            Finally, now we know that Shi Jing 8 is patterned for voiced/unvoiced opposition, as was suspected by F. Tőkei 40 years ago. Is it not nice?

            Of course, it would not be too wise to prove a fundamental law from an irrepeatable or irreproducible event, and it would be even less wise to rearrange bridges according to the new fundamental law. But such serious deeds were not committed here.

 

ACKNOWLEDGEMENTS

            Of course, the investigations mentioned here were not supported by any fund. However the author would like to thank the Theory Department of the Particle and Nuclear Institute of CRIP.

            In different topics different persons are acknowledged for help, collaboration &c. The core of Chap. 2 is a common work with Dr. A. Horváth, Konkoly Observatory, who was one of the original investigators of the ring pattern too. In Chap. 3 Fig. 3.4 is a product of an analysis originally performed within the Hozam és Tárca Bt. About Chap. 4 the work of Ágnes Holba is acknowledged, who was coauthor in the evaluation of spurious scattering measurements; in addition Quantum Gravity discussions with Dr. L. Diósi are highly appreciated. The bulk of the mathematical analysis mentioned in Chap. 5 was done in collaboration with L. Végsö, and very illuminating discussions with Dr. G. Komoróczy are thanked. Finally, in connection with Chap. 6, some advices of Dr. F. Tőkei are acknowledged.

            However the author must take the full responsibility for the conclusions drawn from the analyses mentioned here.

 

APPENDIX A: WEIGHTS FOR CORRELATED MEASUREMENT ERRORS

            Some parts of these considerations can be found in Ref. 6. Consider a measured (say, time) series

              f_i = f(t_i)                                                                                                           (A.1)

Now, some theory (correct or wrong) predicts a form

              f(t_i) ~ F(t_i;p_α)                                                                                      (A.2)

Then f_i measures p_α. Obviously, the measured p_α's are those with which F_i are nearest to f_i. The only question is: in which sense?

            Let us assume that

              1) the theoretical prediction is correct; and

              2) we know the statistic behaviour of measurement errors.

None of them is true, but let us proceed.

            Let us form the measurement error

              d_i º f_i - F_i{at the best p_a}                                                                               (A.3)

In addition, let us assume that the measurement does not distort (if it does, one can correct it), i.e.

              <d_i> = 0                                                                                                        (A.4)

and that the second moments

              <d_id_k> º s_ik                                                                                                  (A.5)

are enough to characterize the statistics.

            Then consider the extremum principle

              S_ik(f_i-F_i)(f_k-F_k)s^ik = Q² = extr.                                                                       (A.6)

where the matrix s^ik is the inverse matrix. One can see that eq. (A.6) is true in expectation values, if s_ik fulfils some definitiveness conditions. E.g. let s_ik be positive definite, and let us assume that one missed the "best" F_i. Then, by extracting a wrong F_i,

              f_i - F_i = d_i + e_i                                                                                                (A.7)

The e's, being misinterpretations, are generally uncorrelated with the measurement errors, so

              <(f_i-F_i)(f_k-F_k)s^ik> = <d_id_k>s^ik +<e_ie_k>s^ik = n + <e_is^ike_k>               (A.8)

The first term is constant, and the second is positive definite, so the total expression takes its minimum at e=0, so at the best F_i.

            If the individual measurements do not influence each other, then s_ik is a diagonal matrix, and eq. (A.6) reduces to the weighted least squares' formula.

 

APPENDIX B: ON THE SUMERIAN SYSTEM OF NUMBERS

            The reader can consult with Refs. 44, 45 and 46. Refs. 44 and 46 agree that 1) the original Sumerian numerical system was not strictly sexagesimal and positional, but 2) it became such, at least in scientific use, either in the late Sumerian or in the early Babylonian times. Ref. 44 gives a multiplication table from the time of King Sulgi (Ur III dynasty), which is strictly sexagesimal and positional. Ref. 45 concentrates on Old Babylonian times, and states that the sign for 0 did not exist in 1500 BC and did exist in 300 BC.

            For our purposes Ref. 46 is the most proper. Let us cite: "The Sumerian system...was sexagesimal in character but not strictly so since it makes use of the factor 10 as well as 6 thus: 1, 10, 60, 600, 3600, 36,000, etc.". And it states that the system of mathematical texts is purely sexagesimal and positional. "The zero was unknown to the Sumerians, and the absolute value of the units was not indicated in the writing, so that a number...4,23,36, can be read either...15,816, or as...948,960, etc...". Ref. 46 gives, however, an older mathematical text from Fara (Suruppak), from cca. 2500 BC, which is not strictly sexagesimal and positional.

            The original text of the Sumerian King List was compiled about 2120 BC, when the transition was still in process from the old system to the new one, and surely used old texts too. The actual copy ends about 1800 BC, in a time when the positional system was dominant. Therefore we can conclude as far at least that the List was a product of an age of changes in numerical systems, and the old system "makes use of the factor 10 as well as 6", not only of 60. These factors are just the ones used in the analysis of Chap. 5.

 

APPENDIX C: ON THE EXPONENTIAL DECAY LAW

            Exponential decay laws can be derived in physics by assuming that atoms or nuclei "do not age". Assume that we have a nucleus, which is, for some quantum mechanical reason, unstable. Then choose a time interval dt. The probability that the nucleus decays between 0 and dt is pdt, where p is a decay rate. Then the probability of decay between dt and 2dt is (1-pdt)pdt and so on. Going to 0 with dt and summing up, the chance that the nucleus is still in existence after t is

              P(t) = e^-pt                                                                                                        (C.1)

which is the exponential decay law if p is independent of t.

            Now, approximately the same is true for usurping generals. They have no dynasty, no tradition, and other generals can follow their examples easily. If so, the probability of being overturned in a period dt if it has not yet happened is time-independent. Average usurpers have no time to make their rule traditional and stable. If one is successful, then he already has founded his own dynasty, and then he counts as a lawful ruler.

 

REFERENCES

 [1]       Schwarzschild M.: Structure and Evolution of the Stars. Princeton University Press, Princeton, N.J., 1958

 [2]       Novotny Eva: Introduction to Stellar Atmospheres and Interiors. Oxford University Press, New York, 1973

 [3]       Fowler W. A.: Nature 238, 24 (1972)

 [4]       L. Ky: KFKI-1996-02/C

 [5]       Baktai Mária, Fejes I. & Horváth A.: Astron. Zh. 41, 413 (1964)

 [6]       Horváth A. & Lukács B.: KFKI-1986-20/B

 [7]       G. E. Williams & C. P. Sonett: Nature 318, 523 (1985)

 [8]       Ch. Spiering & al.: Zeuthen preprint PHE 90-31 (1990)

 [9]       G. Gamow: A Star Called the Sun. Penguin, Harmondsworth, 1967

[10]      R. C. Wilson & H. S. Hudson: Nature 322, 810 (1988)

[11]      J. A. Eddy: Science, 192, 1189 (1976)

[12]      See: The Economist, 13^th July, 1974

[13]      A. Pittock: in Solar-Terrestrial Influences on Weather and Climate. D. Reidel, Dordrecht, 1979, p. 181

[14]      J. M. Mitchell, C. W. Stockton & D. M. Meko: in Solar-Terrestrial Influences on Weather and Climate. D. Reidel, Dordrecht, 1979, p. 125

[15]      J. M. Wilcox: Science, 192, 745 (1976)

[16]      A Century of Agricultural Statistics. Great Britain 1866-1966. Her Majesty's Stationery Office, London, 1967

[17]      B. Lukács: KFKI-1991-08

[18]      B. Lukács: Once More about Economic Entropy. Acta Oec. 41, 181 (1989)

[19]      L. Jánossy, Theory and Practice of the Evaluation of Measurements. Clarendon Press, Oxford, 1965

[20]      Ágnes Holba & B. Lukács: Acta Phys. Hung. 70, 121 (1991)

[21]      F. Károlyházy, Magy. Fiz. Foly. 22, 23 (1974) (in Hungarian)

[22]      F. Károlyházy, A. Frenkel, B. Lukács, in: Physics as Natural Philosophy, eds. A. Shimony and H. Feshbach, MIT Press, Cambridge Mass. 1972, p. 204

[23]      L. Diósi and B. Lukács, Phys. Lett. 142A, 331 (1989)

[24]      L. Jánossy, Acta Phys. Hung. 1, 423 (1952)

[25]      G. C. Ghirardi, A. Rimini and T. Weber, Phys. Rev. D34, 470 (1986)

[26]      G. Berkeley, Treatise on the Principles of Human Knowledge. London, 1710

[27]      Ágnes Holba & B. Lukács: in Stochastic Evolution of Quantum States in Open Systems and in Measurement Processes, eds. L. Diósi & B. Lukács, World Scientific, Singapore, 1994, p. 69

[28]      Th. Jacobsen: The Sumerian King List, Assyriological Studies 11, Chicago, 1939

[29]      A. Poebel: Historical and Grammatical Texts, Philadelphia, 1914, N°'s 6-7

[30]      B. Lukács & L. Végső: Altorient. Forsch. 2, 25 (1975)

[31]      J. E. Morby: Dynasties of the World. Oxford University Press, Oxford, 1989

[32]      W. C. Hayes, M. B. Rowton & F. H. Stubbings: Chronology: Egypt, Western Asia, Aegean Bronze Age. Cambridge 1962

[33]      A. Poebel: Historical Texts. Philadelphia, 1914, 151

[34]      G. Clark: World Prehistory. Cambridge University Press, Cambridge, 1969

[35]      J. Aurifaber: Chronica des Ehrnwirdigen Herrn D. Mart. Luthern &c., Wittenberg, H. Lufft, 1551

[36]      F. Tőkei: Acta Orient. Hung. VI, 53 (1956)

[37]      F. Tőkei: Acta Orient. Hung. VII, 88 (1957)

[38]      F. Tőkei: Sinológiai műhely. Magvető, Budapest, 1974

[39]      B. Karlgren, Grammata Serica Recensa, BMFEA 29, Stockholm, 1957

[40]      G. E. Peterson & H. L. Barney: J. Acoust. Soc. Amer. 24, 175 (1952)

[41]      I. Borbély & B. Lukács: Acustica 68, 52 (1989)

[42]      G. Olaszy: in Proc. 8^th Colloq. on Acoustics, Budapest, 1982, p. 204

[43]      B. Karlgren: The Book of Odes. Stockholm, 1950

[44]      B. L. van der Waerden: Science Awakening, Vol. 1, Nordhoff International Publishing, Leiden

[45]      O. Neugebauer: The Exact Sciences in Antiquity. Brown University Press, Providence, RI, 1970

[46]      S. N. Kramer: The Sumerians. University of Chicago Press, Chicago, 1963