ARE WE CHIMP HYBRIDES? AND THEN THE HYBRIDES OF CHIMPS AND WHOM?

 

B. Lukács

 

Matter Evolution Subcommittee

 

of the Geonomy Scientific Committee of HAS

 

CRIP RMKI

 

H-1525 Bp. 114. Pf. 49. Budapest, Hungary

 

lukacs@rmki.kfki.hu

 

ABSTRACT

            According to a recent article we are the offspring of proto-chimps and superhuman Sahelanthropi. Still the chimps and we live; the superhumans died out. (Or did they emigrate into the Galaxy? Probably not.) Evolution is not so simple as Darwin imagined it; against the recent article Huxley and St. Thomas of Aquinas would have fought side to side. But we must learn from facts what was our evolutionary pathway. And enjoy a paper of mine from 1990 about back-hybridisation: I had to translate it from ChiWriter to put it to the Net.

 

1. INTRODUCTION

            A recent article in Nature Online ([1]; surely now it must exist on paper format too, but that I must check) seriously have disturbed our traditional opinions about "hominisation". Until now in practically any framework of thinking (theological as well as philosophical as well as scientific) the divergence of "human" and "nearest animal" lineages was considered as an important step and the emergence of a "human" line was considered a qualitative change. Now it seems that even that step was something "neutral".

            4 species are extant which are relevant for hominisation: gorilla, the two chimp species (common chimp & bonobo) and we humans. I deliberately use everyday names because correct taxonomy is still a matter of discussion, and the ambiguity would disturb the present article. Anyway, the above 4 species are rather near to each other, genetic distances are small and divergence times seem to remain below 7 My. All recent data support that the extant lineages diverged in the following sequence.

            1) Gorilla line diverged from the still common lineage of chimps & us. You may put the PoD at cca. 7 My. (Ref. [2] gives 6.3±0.6 My.)

            2) The common lineage of chimps diverged from the lineage leading to us. In "traditional" scenarios (so in all studies until [1]) this is the Emergence of Man. The PoD is put generally to 5-6 My. (Ref. [2] gives 5.1±0.8 My.)

            3) Then the two chimp lineages diverged at cca. 3 My.

            Of course lots of extinct lineages may have existed too, but one cannot perform genetic investigations about them, and, if these lineages were unsuccessful, maybe they were not overly important.

            Now, Ref. [1] gives hard data which should be ordered into some clear pattern. The first and maybe simplest attempt has led to the weakening of the traditional picture. I will discuss briefly this in Chapter 2., In Chap. 3 I call attention to a paper from 1990 [3], which I have appended to this site.

 

2. ON THE EVOLUTIONAL NOIVELTIES IN REF. 1

            Ref. [1] suggests 2 major innovations in "hominisation" picture. First, there seems to be a (restricted) trifurcation in a triangular pattern at the separations of the gorilla, chimp and human lineages. Second, after the divergence of chimp and human lineages (restricted?) interfertility remained for a long time, and the present humans are descendants of an interspecific hybridisation. The two novelties are connected: triangular trifurcation clearly indicates a retained interfertility, as we are going to see.

            GCH trifurcation is not new. Some quarter century ago comparisons of primate chromosomes (forms & fluorescent band technique) showed into the same direction. H chromosomes differ from both C and G ones, but in two different ways. First, the H set is 2*22+XY, while both C and G ones are 2*23+XY. Obviously a central fusion/Robertson translocation happened somewhere on the way leading to solely us. Clear data show that our Chromosome 2 is a result of fusion of 2 C chromosomes [4], [5]. Second, there are a few inversions between C and H and roughly the same number between C and G and G and H. Now, the reconstruction of the sequence of these inversions among G, C and H [4] resulted in a triangle; at least for one inversion we seem to inherit G pattern.

            Obviously the genome gives much more insight into the evolutionary path than simply the structure of chromosomes. While the complete gorilla genome is not yet at reach, the authors of [1] compared all the sequences where H, C and G sequences were all available. Now, the result is again a triangle. While our closest relative is chimp, there are some sites where H and G sequences are the same but C differs. And these "anomalous sites" are no rare exceptions: [1] tells that their amount is 23±5 %.

            So much back mutation or independent agreement is impossible. So if we preserved G sequences against C ones, then G, C and H lineages cannot be ordered via two clearcut cleavages: G vs. CH and C vs. H. The details of this triangular structure, however, will not be clear until the collection of the complete gorilla genome.

            As for the second novelty, the authors of [1] (if I understood correctly the rather short paper) perform mainly population genetics calculations, and get results contradictory to simple situations. E.g. the X chromosome is "too young"; its divergence time is too short. To be sure, X is expected to be younger than the autosomes, because males have only one; but the X is younger than expected.

            Now, [1] suggests a history. In it, human-chimpanzee divergence "happened twice". There was a first divergence at t₁>6.3 My, resulting in two divergent lineages, say, P and R. Then, later, at t₂<6.3 My, P and R hybridised, resulting in Q. Obviously this is possible if, say, t₁-t₂<1 My. (Between horse and ass, where the divergence time is ≈2 MeV, the hybrid is almost fertile, see individual stories from Aristotle to present.) However, now we have only P, the chimpanzee, and Q, the humans! R has died out.

            Unfortunately the smoking gun has not yet found, or at least not published in [1]. That would be the distribution of divergence times or normalised ratios of differences or something similar for many sections of chromosomes. Namely, the divergence times calculated from different pieces of the DNA always have some smooth distribution, even if there was a unique time of speciation, for elementary probability reasons. However the distribution should be something with a single peak. But if you see two peaks...

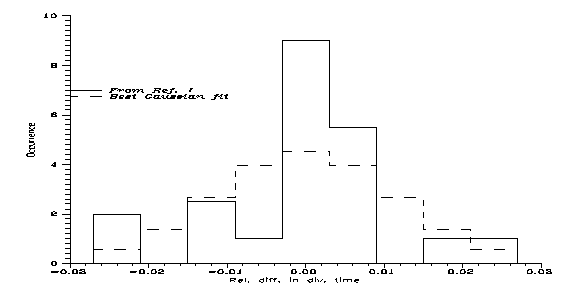
            The thing most similar to this is the uppermost graph on Fig. 1 of Ref. [1], showing the relative rates of human-chimpanzee differences calculated for individual chromosomes. Unfortunately no numbers are given, so we can use only the graph; and for the little chromosomes 14-22 only an average is given. Even then, omitting the details, from them one gets my Fig. 1. The continuous line is the empirical distribution in 0.06 bins of relative differences (around the global autosomal average normalised to 1) and the dashed line is the best Gaussian fit to it. Since the Gaussian or normal distribution fairly approximates lots of distributions obtained in simple models of randomness, one would expect something fairly Gaussian; but no. True, the average difference is most abundant, but both much more and much less differences are enhanced while medium differences are suppressed. For first sight this would suggest 3 important speciation events, not 2; but maybe crossovers are behind. Indeed, a nontrivial speciation process is indicated.

 

 

 

 

 

 

 

 

 

Fig 1: The distribution of normalised divergence times between H and C chromosomes; autosomal average is 1. (For Chromosome X it is 0.835.) Observe the serious deviation from Gaussian distribution.

 

 

 

            The authors try to calculate some bounds for primordial speciation and then for back hybridisation; the estimates are not very strong but interesting. It seems that the divergence time may go up even to 7.5 My. Now, recent calculations with a simple speciation event give generally 5-6 My, and the overpopulation in the distribution appears above 0.2. so some 2.5 My would separate the two events. Long enough, similar separation of horses and asses resulted in practical infertility, but facts are facts...

            For any case then indeed the first speciation can go before Toumai, the Sahelanthropus (?) tchadensis and that lineage later died out. However there are two disturbing consequences, disturbing even if they do not rule out this scenario.

            First, any HC split early enough for Toumai will be before the HCG split too. Namely, look at [2]. The paper concentrates on divergence times and gets 5.1±0.8 My for HC and 6.3±0.6 My for (HC)G. So even in the orthodox scenario the two divergence times marginally merge. This is not bad considering the 23±5 % of the genome where the gorilla DNA is nearer to us than the chimpanzee one is; but also it demonstrates that the scenario of Ref. [1] on its Fig. 1 is not self-consistent. At a primordial human-chimp split led to Toumai the proto-gorillas were still fertile with the (HC). And anyways: how do you expect to distinguish human, chimp or even gorilla lineages 6.5 My ago if gorilla was separated from our lineage at 6.3 My? It is a nice question if Toumai was Sahelanthropus or Sahelpithecus [6]; but for that age the question is of course anachronistic.

            Second: the lineage more different from chimps, so superhuman is now extinct, while we, carrying more chimp DNA, are paramountly successful. Possible; but then we should not be so proud about the split from the chimps. Darwin and Huxley imagined it otherwise; but now it looks as if in the first 1-2 million years our ancestors were not superior to chimps (if not the opposite...).

            By the way, we shall not be able to formulate clear sentences about hominisation until we do not define the meaning of "hominisation". This was not difficult until cca. 1985, when Genus Homo was believed to have appeared some 1.5 My ago from Australopithecus. But look again at [2]. There the exact Linnean names of common chimp, bonobo and us are Homo troglodytes, Homo paniscus & Homo sapiens, respectively; the other homines differ only from us on subgeneric level, not going into the proper names. Then according to the rules of lingua Latina hominisatio is the evolutionary process resulting in Genus Homo, so chimps also underwent it. This usage is contrary to Common Sense;  but, on the other side Common Sense is now contrary to grammar...

 

3. ON LIMITED FERTILITY DUE TO ROBERTSON TRANSLOCATION

            There was a Robertson translocation on the way from the LCA of chimps and us to us. Namely our Chromosome 2 is a fusion of 2 chimp chromosomes. Such a Robertson translocation does not cause mutual sterility as many well documented cases prove it, including familiar enhancement of Down syndrome caused by a 15+21 fusion. The parent is normal, but his/her 15+21 may be detected in the mitosis/meiosis after fertilisation. So the child may inherit 3 21's (one on a 15), and so Down. With a bigger chromosome trisomy can be lethal.

            We do not know when this Robertson translocation happened; but surely it was behind one divergent evolution. In 1990 we calculated the consequences in a scenario where this mechanism was behind the human-chimp divergence. It may have been; and as you will see, it causes reduced interfertility but no more.

            Having read [1] I looked for the old file. Alas, it was written in ChiWriter, with Grapher figures, so it was nontrivial to make it Internet-friendly. Now it is ready and is given here as an insert; enjoy it if you like.

 

************************************************

 

From: From Cosmogenesis to Biogenesis; Proc. of the 1^st Symposium on Matter Evolution, KFKI-1990-50, pp. 125-129

 

HOW TO JUMP INTO HUMANITY: A MATHEMATICAL RECONSTRUCTION

Ágnes Holba & B. Lukács

Central Research Institute for Physics, H-1525 Bp. 114. Pf. 49.

Budapest, Hungary

Received on 5^th Oct., 1990

 

ABSTRACT

            Judged from the chromosome sets, one of the factors responsible for the appearance of a separate human line of evolution may have been a Robertson translocation. Here this step is analysed and some constraints are obtained for the parameters valid then and there.

 

1. INTRODUCTION

            The previous paper (Kordos, in this Volume) extensively discussed the hominization process in the light of fossils and observed environmental changes, and the reader has got a coherent picture about an evolution of cca. 40 Mys leading to ourselves.

            However, about the last big "jump", separating the Hominids from their "ape" relatives (called colloquially Pongidae), fossils are silent: nothing has been found between 8 and 4 Mys. So this event

can only be reconstructed from observed tendencies and recent data.

            At the beginning of the separate hominid branch there must have been at least one very exceptional step as judged from some paradoxical features of the endproducts. For example: the genetic distance between Homo sapiens and the great African apes is in the order of that of close congeneric or even sibling species [1], [2], [3]; in contrast, taxonomically they are classified into separate families.  The estimated time of separation changes between the 25 Mys of fossils put into traditional taxonomic context and 4 Mys of distance in immunology [4], [5]. It is hard to decide if the man-chimpanzee-gorilla separation was a trifurcation or two bifurcations [6], [7]. (Two subsequent bifurcations would anyways lead to strange result. If the human lineage had been detached first, then that would be expected to preserve the primitive features, i.e., say, bipedal locomotion would be ancestral to knuckle-walking of African apes. In any of the other two cases man would form a taxonomic unit with one ape against the other one.)

            And, in spite of the greater similarity in immunology between Homo and African Pongidae than between African and Asian ones [5] [8] all Pongidae have 23 pairs of autosomes while recent hominids have only 22.

            The last fact indicates a Robertson translocation (or central fusion), which may be a natural explanation for some other peculiarities as well. E. g. such a translocation creates a fertility barrier between two subpopulations carrying the same genes, so can create two species even at very small genetical or biochemical distances. However, the same fertility barrier impedes the survival of such a mutation. Therefore the fate of a Robertson translocation always depends on a lot of parameters, and can be predicted only if all the parameter values are known. However, now we are in a topsy-turvy situation: we know that the fusion has propagated in the population, and try to find out why and how. By other word, the success of the mutation singles out a domain in the parameter space at 5 Mys ago, and we are looking for the actual domain.

            In a fixed model this is a pure mathematical problem, and, indeed, we will try to restrain ourselves from biologic discussions as far as possible. However, it is not always possible because one has to select a specific model, with a restricted number of parameters, which involves technical simplifications &c., and this selection needs some biological considerations anyways. If the simplifications were too crude, the calculations could be repeated with less simplifications as well.

 

2. SOME ELEMENTARY FACTS

            There are claims to have found the evidences for a Robertson translocation in hominisation. For a review see Refs. 2 & 7. According to it, human and chimpanzee chromosomes can be brought into correspondence by band technique, with the result that the difference is a number of pericentric inversions, and a central fusion of two chromosomes, originally small and acrocentric, resulting in the large metacentric human Chromosome 2. According to the genetic distances and estimated mutation rates, Refs. 5 & 6 place the separation of human and chimpanzee-gorilla lineages to -5 Mys, so this is the earliest possible date of the fusion. Ref. 7 shows 6 Robertson translocations in the catarrhyne evolution on the branch ending in us, which means roughly one in each 10 Mys. Therefore, while analogous mutations do happen in each generation (cf. the rare inheritable kind of Down syndrome), the survival of the mutation is rare indeed.

            Since the fusion is absent in any Pongida, it must have happened in the separate human evolution. Ref. 6 estimates a common gorilla-chimpanzee branch for further 2 Mys, but the problem is that Ref. 7 sees some chromosome changes shared by man and chimpanzee, but not by gorilla, while some ones indeed characterize solely the chimpanzee and gorilla. Therefore it seems that there remained some restricted cross-breeding even after the separation of the human branch, and also the gorilla and chimpanzee subbranches were then already distinguishable. To be cautious, it is enough to state that the situation indicates a complicated genetic history.

 

3. ROBERTSON-TRANSLOCATION

            Consider an animal whose chromosome set contains, besides arbitrary others, two pairs of acrocentric chromosomes (A A, B B). Assume a coincidence of two fragmentations: A loses a very small terminal fragment but retains the centromere, while B breaks losing just the centromere and the irrelevant terminal part behind. After inverse recombination the mutation changes the pair into (A AB, B ba).

            Here AB contains the full information of A and B, containing the centromere of A, while ba is blank, irrelevant, with the centromere of B. Therefore the mutant produces four kinds of haploid  gametes, listed below. By pure combinatorics the four probabilities would be equally 1/4, but observations clearly show a moderate preference to the mutant descendents. The simplest way to describe the phenomenon is the meiotic scheme of Table 1, and this simplest meiotic scheme will be used in our model.

 

AA;BB	→	A;B	p=1
AAB;Bba	→	A;B	p=(1-k)/4
AAB;Bba	→	A; ba	p=(1+k)/4
AAB;Bba	→	AB;B	p=(1-k)/4
AAB;Bba	→	AB; ba	p=(1+k)/4
AB AB; ba ba	→	AB; ba	p=1

 

Table 1: The simplified meiotic scheme

 

            Here 0≤k≤1 is the preference parameter (of any origin); for some other translocations of the recent human set [7] k~0.2, and we will use this number in some numerical examples, but do not regard it anything more than an estimation.

 

4. THE PROPAGATION OF THE FUSION

            Now we are going to define the model step by step. Consider a population with 3 different genotypes, their relative concentrations and fitness factors (meaning the ratio of life expectancies in reproductive age), as follows. Wild form: (n₀,1), heterozygote mutant:  (n₁,v), homozygote mutant: (n₂,w). Now we assume random mating, and mutation only in the ova, with probability ε. Then the concentrations change from generation to generation as

 

n₀ → Q(1-ε)[n₀+(1-k)vn₁/4]

n₁ → Q{(2-ε)[(1+k)vn₁/4+wn₂][n₀+(1-k)vn₁/4]+ε[n₀+(1-k)vn₁/4]²+(1-k²)v²n₁²/8}

n₂ → Q{[(1+k)vn₁/4+wn₂]²+ε[n₀+(1-k)vn₁/4][(1+k)vn₁/4+wn₂]}                                  (4.1)

Q^-1 ≡ (n₀+vn₁/2+wn₂)² + (1-k²)v²n₁²/8

 

            Fixing the parameters v, w and ε, the concentrations can be calculated step by step from an initial condition. Now we want to go back, calculating the parameters from the final result, but even then estimations for the suspected ranges are needed. For the analogous hereditary Down syndrome ε~10^-4-10^-5   which may be so also for now, and we mentioned above a guess for k. However, v and w cannot be read off because they obviously depend on the gene content of the chromosomes; the considered fusion is over and cannot be anymore observed. As for the initial conditions, the obvious ones would be n₀≈1, n₁≈0, n₂≈0  ("before fusion"). However, as we shall see, this state never existed, and such initial conditions may be incompatible with the known final result.

            To reduce the number of unknown parameters, we assume that the change in fitness is proportional to the changes themselves:

 

w=1+2(v-1)                                                                                                     (4.2)

 

With this now let us postpone the values of v and w for a moment.

            The structure of eq. (4.1) is quite similar to that of systems of differential equations. In that case it is often observed that in asymptotic time the actual solution becomes independent of the details of the initial condition, but there are different asymptotic solutions for very different initial conditions. This is so in the present case too. E. g. for ε=0 eq. (4.1) has 3 stationary solutions: i) n =1; ii) n =1; iii) a third solution obtained if we write the same concentrations on both sides (details later). The obvious expectation is that these final states belong to different domains of initial conditions. Then there is a stationary state reached asymptotically from the "natural" initial conditions. After some transient behaviour this state is well approached and will not change if the parameters are constant. So if a change happened say 5 Mys ago, then there must have happened something either with the parameters, or with the actual state by a surprisingly high fluctuation. The first guess is v≈w≈1, because the genes are unchanged. Then the asymptotic solution belonging to the initial condition n =1 is:

                    

n₁ ≈ 2ε/(1-k), n₂ ~ ε²                                                                                        (4.3)

 

So for any reasonable k the mutant concentrations remain very low forever, indeed. Then one is tempted to argue for v»1, judged from the present serious advantage of man to chimpanzee. While it is strange without gene mutation, it is by no means impossible; Ref. 2 demonstrates that even now the genetic distance between the two species is very moderate and still the difference is serious. The last paragraph of Ref. 2 even suggests position effect as cause for the serious difference, and this does appear via Robertson translocation. However the fitness w of the human ancestor 5 Mys ago must not be identified with that of the present man, with his technology &c. And, by assuming high constant v and w values one gets the asymptotic solution n₂≈1 in a few generations (details later), i.e. then the wild form practically cannot have existed at all.

 

5. TWO SCENARIOS

            So there seem to remain only two possible scenarios (together with their combinations, of course). One is the transient increase of v. While one cannot wait serious increase from pure position effect, there can be a very special difference leading to definitely higher v under very special circumstances, which can exist, of course, only for limited time. Then we have to check if this transient increase is enough to produce the final homozygote mutant population by "the survival of the fittest". The other scenario is massive inbreeding (Adam & Eve), sometimes suggested.

            In it v=1, but the mutant must have been isolated from the population together with arbitrary number of the opposite sex. Then in the next generation

 

n₁/n₀ ≈ (1+k)/(1-k)                                                                                                       (5.1)

 

In the next step the fertility barrier of the heterozygotes already appears, so this scenario is equivalent with a very high initial n₁ value, with n₂≈0.

 

6. RESULTS AND CONCLUSIONS

            Consider the first scenario. Originally for an indefinite long time v≈1; so we start from (4.3). At t=0 v increases (for a while).

            Let us see first the condition for the propagation of the mutation. Solving the evolution equations for the beginning (n₁«1, n₂«n₁) one obtains that n₁ remains growing above a level ~ε if

         

v>2/(1+k)                                                                                                                                (6.1)

 

So without the meiotic preference parameter v>2 would be needed, and the neighbourhood of v=1 can be reached only if k≈1, which could happen only with improbably special meiotic mechanisms. The meiotic preference of Robertson-translocated mutants helps the propagation of the mutation, but in itself cannot do propagate it.

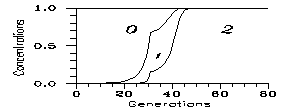
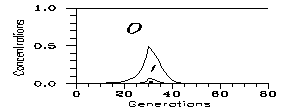
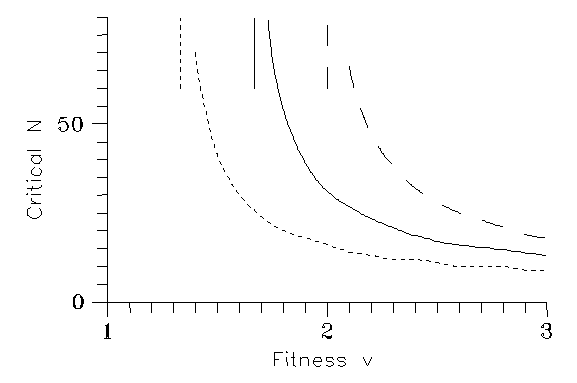
            Then in most cases the mutation dies indeed out, i.e. under general circumstances the mutant concentrations are cca. on the level (4.3). Now we are going to discuss the special circumstances compatible with propagation. For a short time v must have exceeded the threshold value (6.1). Assume, therefore, that after N generations v (and w) returns to 1; Fig. 1 is a calculation for v=2. One sees that if the favourable conditions remain for 30 generations, the new species dies out after some further 30 generations; however, raising N from 30 to 31, the new species survives and the old one will die out. The critical N value obviously decreases with increasing v; a numerical calculation leads to Fig. 2 for k=0.2.

            These results suggest that the sudden change in the fate of the two species happens at such a duration of the favourable conditions when the concentrations of the mutants have been able to reach some critical values. Here we have arrived at the position to decide the possibility of the Adam&Eve scenario as well. Since this problem is important enough, we are going to determine the critical n values as functions of k (for definiteness' sake, at ε=0, which is a good approximation at already substantial mutant concentrations).

            Setting v=w=1, below a critical value the mutant concentrations decrease, above they increase. (For a stricter statement see the Appendix.) First we may look for the equilibrium concentrations which can remain unchanged. To get them one has to write the same n values on both sides of the evolution equations, which then give 2 algebraic equations for the two independent concentrations. The calculations show that the equations have only one root pair (if any) for any fixed 0<k<1 in the possible domain 0<n₀,n₁,n₂<1. The result is Fig. 3.

            Now, this equilibrium may be stable or unstable; this question can be answered by starting a calculation in the neighbourhood of the critical concentrations. This perturbative calculation can be analytically performed (cf. Appendix), with the result that the equilibrium is always unstable (except for domains of zero measure). This  result may be interpreted in the following way. If one of the homozygotes dominates the other then the minority is continuously being eaten up. For definiteness' sake, assume that n₂

is dominant. Then the heterozygote subpopulation (1) cannot maintain itself due to the reduced fertility. As for (0): (01) pairs result in (0) only in 50%, while all (02) pairs give (1).

            Being (2) dominant, (22) pairs are more frequent than (00) ones, so (2) wins. (Therefore after the new population is established, any border encounter of the populations ends without a mixed population; the two disjoint "species" remain disjoint, but with a limited possibility of gene exchange, which decrease the genetic distance, to be remembered.) The critical concentrations, whenceforth (2) is dominant, of course depend on the preference factor k of the meiotic processes, and just this dependence was calculated.

            In our case it turns out that  (except for domains of 0 measure) for ε=0, v=w=1 the plane of initial conditions (n₁,n₂) is divided into two regions: below  the dividing line the final fate is n₀=1, above it is n₂=1.

            Now we have explored our model system, so, with the utmost caution, are in the position to draw some conclusions. In the scenario "survival of the fittest" for k=0.2 the final result is Fig. 2; with higher k values the needed N decreases. It is definitely outside the scope of the present paper to guess if the unknown necessary environmental conditions helping the mutant could be present for the calculated time.

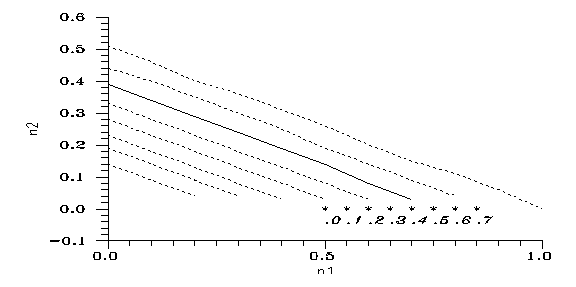
            In the scenario "Adam&Eve" (or rather Adam or Eve) the conclusion can be obtained by putting the initial condition (5.1) onto Fig. 4. It turns out that for a complete isolation the critical k value is ≈0.35. Incomplete isolation is almost hopeless; with a second person of the same sex n₁/n₀ is roughly halved and the point  gets out of the preferred domain except for k's close to 1.

            Now, this possibility can in principle be checked by observations. If any fusion is seen in the present human population with k>0.35, then the scenario is possible, and the fusion is propagated just when the mutant is isolated and the subpopulation does not die out. For this, an isolated Adam is much better than an isolated Eve, of course. Being n₁ in the order of ε, this isolation is very improbable, but this fact may be conform with the observed rate 1/10 Mys.

            If the meiosis cannot produce k>0.35, then the second scenario is ruled out in the present simplest model. More complicated meiotic schemes may help, but it is better not to hope in meiotic processes handmade directly for the propagation.

            After the propagation of the mutation a new population has appeared with a chromosome number less by one pair. However this propagation was not necessarily worldwide. Some generations later there is again a possibility for mixing in peripherial encounters. This means a new initial condition n₁=0. The result is on Fig. 7 for k=0.2: one of the original constituents of the mixture dies always out in cca. 10 generations. However, during these generations a serious gene transfer is possible, thus keeping the genetic distance low.

 

ACKNOWLEDGEMENT

            One of the authors (B. L.) acknowledges some discussions in the beginning of 70's with L. Végső  about numerical simulations of the propagation of a central fusion.

 

APPENDIX: EVOLUTION IN THE NEIGHBOURHOOD OF A FINAL STATE

            Here we give a detailed mathematical analysis of the possible asymptotics of paths governed by eq. (4.1) in the case ε=0, v=w=1.

            Eq. (4.1) is two equations for two variables as can be seen by eliminating n₁=1-n₀-n₂. It is worthwhile to introduce two independent new variables x and y:

 

            n₀ =(x+y)/2; n₁ =1-x; n₂ =(x-y)/2                                                                                              (A.1)

      

and then  for ε=0, v=w=1 (which condition will not be repeated henceforth) eq. (4.1) reads as

           

x_i+1 = {Q(x)[(1+x)²+(2y-k(1-x))²]/8}_i

y_i+1 = {Q(x)(1+x)(2y-k(1-x))/4}_i                                                                                              (A.2)

Q(x) = 8[2(1+x)²+(1-k²)(1-x)²]^-1

 

Requiring equality of sides one gets the stationary solutions, i.e. the possible final states. The roots are as follows:

 

(x,y)=   (1,1);     (1,-1)    (x₀,y₀)                                                                                                (A.3)

                                  

where

 

{(3-k²)x₀³ +(1+k²)x₀² +(1+k²)x₀ -(1+k²)}{(3-k²)x₀ +(1+k²)}²-

-8k²(1+x₀)[(3-k²)x₀²+2k²x₀ +(1-k²)] = 0                                                                                  (A.4)

y₀  = 2k(1+x₀)/[(3-k²)x₀ +(1+k²)]

 

The equation for x₀ depends only on k². For k²<1 it has only one root in the domain 0≤x₀≤1, and in addition for |k|>0.5 this root gives such a y₀ which leads to  the negativity of one of  the ni's. For k>0 the root is displayed on Fig. 3; the k<0 case can be obtained by the exchange of n₀ and n₂.

             Now choose a possible final state and assume that the population is already in the neighbourhood. Then

 

x ≡X + ξ; y ≡Y + η

 

where ξ and η are small of first order and we calculate up to first order. Then eq. (A.2) reduces to a system of homogeneous difference equations. Because of the homogeneity, the changes slow down without limit going to the root. Then there one can substitute the difference equations by differential ones as

                   

ξ_i+1 = ξ_i + (dξ/dt)dt                                                                                                                   (A.5)

 

and we will measure the time in generations. A system of two homogeneous linear differential equations of constant coefficients has the solution

        

ξ= Ue^λt +Ve^μt; η= We^λt +Ze^μt                                                                                                   (A.6)

 

where λ and μ are the solutions of a quadratic equation; either both are real, or they are complex conjugates (periodic solution).

            The differential equations give two relations among U, V, W and Z, and the remaining two can be determined from the initial conditions ξ(t=0), η(t=0).

            For the first two final states of (A.3) one obtains

 

λ = (-1±k)/2; μ = -1                                                                                                                 (A.7)

 

Both exponents are negative in both cases, therefore the states approach the final state with a half life time cca. 1 generation.

            For the third final state (if exists) one gets

 

(dξ/dt) = (a-1)ξ+ βη

(dη\dt) = γξ+ (d-1)η                                                                                                                (A.8)

 

with

 

Aα = -2(3-k²)x₀² +4ky₀+2(1-k²)

Ab= 4(kx₀ +2y₀-k)

Ag= -2(3-k²)x₀y₀+4kx₀+2(1-k²)y₀                                                                                            (A.9)

Ad= 4(x₀+1)

A  = (3-k²)x₀²+2(1+k²)x₀+(3-k²)

 

Then for the exponents one gets

 

            λ = [a+d-2+((a-d)²+4βγ)^1/2]/2

μ = [a+d-2-((a-d)²+4βγ)^1/2]/2                                                                                                            (A.10)

 

 

Now, if both exponents are negative, then from anywhere in the neighbourhood the path approaches the equilibrium point; if both are positive, then all paths are repelled, so the equilibrium point is unstable. However, there is a third possibility, when λ>0 but μ<0. In this case from most initial conditions the paths are repelled, but from the special ones, when U=W=0 they are attracted. These initial conditions lie on the line

 

(μ-a+1)ξ(0) - βη(0) = 0                                                                                                          (A.11)

 

which is a domain of 0 measure. Of course, these statements are valid only in the neighbourhood of the state.

            So in general the plane of the independent initial conditions is divided into 3 domains: from "below" the paths go into n₀=1, from above into n₂=1, and from a neighbourhood of (x₀,y₀) they may go into that point. If both λ and μ are positive, this domain is absent, and if only μ is negative, it reduces to a domain of 0 measure (a section of a line). Fig. 4 displays the border of the "upper" domain; the signs of the exponents can be found numerically. In our case for 0<k<1 one exponent is always positive; the other is negative up to k≈0.85. However, from k≈0.5 the equilibrium point (x₀,y₀) is already outside the domain of possible concentrations (n_i≥0). Therefore the third domain exists whenever the equilibrium is possible at all; however it is always reduced to 0 measure, and can be ignored from practical point of view.

 

REFERENCES

 [1]       Elisabeth J. Bruce & F. J. Ayala: Nature 276, 264 (1978)

 [2]       M. C. King & C. A. Wilson: Science 188, 107 (1975)

 [3]       M. Blanc: La Recherche 15, 654 (1984)

 [4]       V. M. Sarich & J. E. Cronin: in Molecular Anthropology (eds.  M. Goodman & R. E. Tashian), Plenum Press, N. Y. 1976, p. 141

 [5]       V. M. Sarich & A. C. Wilson: Science 158, 1200 (1967)

 [6]       N. Barton & J. S. Jones: Nature 306, 317 (1983)

 [7]       B. Dutrillaux: La Recherche, 12, 1246 (1981)

 [8]       M. Goodman: in Phylogeny of the Primates (eds. W. P. Luckett  and F. S. Szalay), Plenum Press, N. Y. 1975, p. 219

 

 

 

 

 

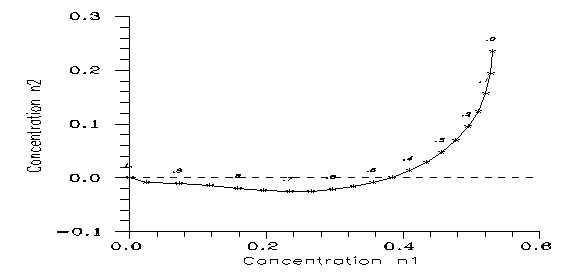
Fig. 1: Evolutions for k=0.2, v=2 for N generations (afterwards v=1). N is 30 on left and 31 on right. 0: wild (in our case 48 chromosomes), 1: heterozygote mutant (47), 2: homozygote mutant (46).

 

 

 

 

 

Fig. 2: Critical number of generations N vs. fitness v; k=0 (dash), 0.2 (solid), 0.5 (dots). The vertical lines indicate N=∞.

 

 

 

 

 

Fig. 3: Equilibrium points on the plane (n₁,n₂). Parameter k is given for any fourth star.

 

 

 

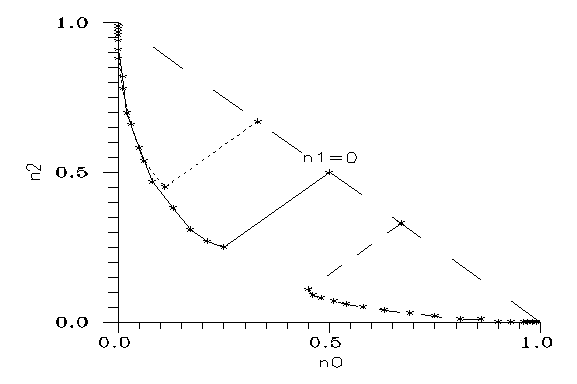
Fig. 4: Critical line(s) on the (n₁,n₂) plane, for the respective k values, from 0.0 to 0.7 in 0.1 steps, right to left (line k=0.2 is solid). From above the respective line evolution ends in n₂=1. Stars: initial conditions of Adam&Eve scenario, k given.

 

 

 

 

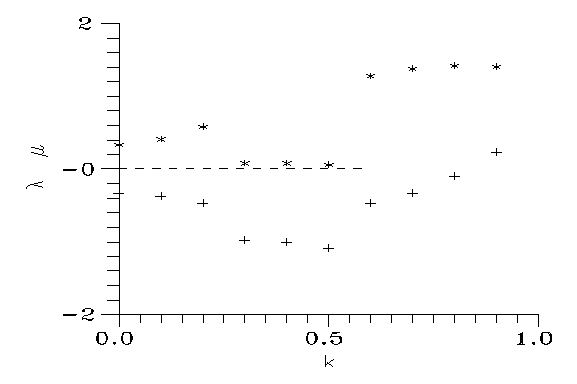
Fig. 5: Exponents λ  (*) and μ (+).

 

 

 

 

 

 

 

 

Fig. 6: Adam&Eve paths, steps by generations, for k=.0 (ó), =.2 (*) and .4 (¨).

 

 

 

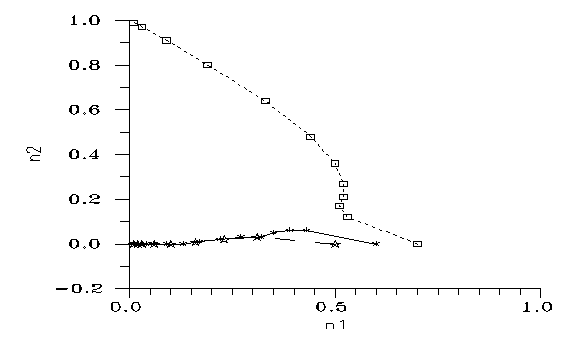
Fig. 7: Evolutions  from mixtures of two monozygote populations. Step: 1 generation.

 

 

 

 

 

 

 

************************************************

 

4. OUTLOOK

            As you can see, a Robertson translocation may lead to restricted interfertility even without changes in genes. In this model we can easily simulate the second event of the story of [1]. Namely, assume first a process during which the human Chromosome 2 was formed and in a subpopulation the 2*22+XY pattern was stabilized. The insert (i.e. Ref. [3]) demonstrates that it was far from trivial; but anyways it did happen once between the LCA and us. Then the two new populations (with 2*22+XY and 2*23+XY, respectively) drifted apart and lived separate lives for ~1 My. If we want, we may call the 48's proto-chimps and the 46's proto-people (proto-humans, being formed from the word "homo", again I should apply to the common ancestors of chimps and us, according to Latin & taxonomy.) Now, some parts of the two populations meet. This is the situation explicitly calculated on Fig. 7 of the insert.

            We can see that (roughly) the chromosome number of the majority will win after ~10 generations. But during that almost anything may happen, meaning gene transfer between the two subgroups of the "chimps" and "people". After that the genome would be a mess for traditional population geneticists.

            And yet: why did Toumai's branch die out? Because it was less similar to chimps? Disturbing...

            We are just organising a Workshop. After that I may append something new.

 

 

 

 

REFERENCES

 [1]       N. Patterson & al.: Genetic Evidence for Complex Speciation of Humans and Chimpanzees. Nature Online May 17, 2006, doi:10.1038/nature04789

 [2]       D. E. Wildman & al.: Implications of Natural Selection in Shaping 99.4% Nonsynonymous DNA Identity between Humans and Chimpanzees: Enlarging Genus Homo. PNAS 100, 7181 (2003)

 [3]       Ágnes Holba & B. Lukács: How to Jump into Humanity? KFKI-1990-50, in Proc. 1^st Symp. on Matter Evolution "From Cosmogenesis to Biogenesis", p. 125

 [4]       B. Dutrillaux: Les chromosomes des primates. La Rexcherche 12, 1246 (1981)

 [5]       J. J. Yunia, J. R. Sawyer & K. Dunham: The Striking Resemblance of High-Resolution g-Banded Chromosomes of Man and Chimpanzee. Science 208, 1145 (1980)

[6]        M. H. Wolpoff, Brigitte Senut, M. Pickford & J. Hawks: Palaeoanthropologu (communication arising): Sahelanthropus or 'Sahelpithecus'? Nature 419, 581 (2002)