IS THE ANOMALOUS BROWNIAN MOTION SEEN IN EMULSIONS?

IS THE ANOMALOUS BROWNIAN MOTION SEEN IN EMULSIONS?

Ágnes Holba and B. Lukács

Central Research Institute for Physics, H-1525 Bp. 114. Pf. 49., Budapest, Hungary

Originally published in: Acta Phys. Hung. 70, 121 (1991)

ABSTRACT

Experimental information is gathered about the so called spurious scattering, a phenomenon of obscure origin in emulsions which is sometimes suspected to be of quantum stochastic origin. In the investigated sample the effect is fairly significant. Comparisons to quantitative models for spontaneous wave packet reduction are made with the result that familiar models cannot explain the amplitude of observed anomalous Brownian motion, however the hope of a more sophisticated explanation is not ruled out.

1. INTRODUCTION

While Quantum Mechanics (henceforth QM) gives correct results for a great number of observables, conceptually the theory contains a disturbing dichotomy, often referred as Problem of Measurement. After half a century continuous discussion it would be ridiculous to go into details. We only recapitulate that the wave function Ψ is governed by the Hamiltonian H. In the lack of self-interaction (as generally assumed) H does not contain Ψ, therefore the equation is linear. Then consider a situation when the microsystem Ψ evolves freely for a time, and then is measured by a macroapparatus. It is easy to prepare such situation that just before the measurement Ψ be in a superposed state of different eigenstates of the physical quantity to be measured. If the apparatus measures faithfully, and if the total H does not contain the wave function, then the final state of the coupled system will contain superpositions of macroscopically different pointer positions, never seen. (Such states may appear only in Everett's rather solipsistic scheme [1], seldom accepted.)

In the '30's von Neumann gave a clear prescription. It tells that Measurement is a very special process outside the regime of the Schrödinger equation. That equation acts between Measurements; during one the wave function jumps into an eigenstate of the operator of the measured quantity with a probability which is the weight of that eigenstate in Ψ.

This prescription works correctly but in it a very expressed dichotomy (evolution vs. jump) has appeared. At least some suggestion would be needed for the switching mechanism. Two suggestions are widely accepted. The first is that the jump (called henceforth Reduction) in Measurement is the action of Mind involved. Then one arrives at the very confusing paradoxes of Schrödinger's Cat [2] or Wigner's example with 2 observers communicating only after the second Measurement [3]. If an explanation leads to paradoxes then it is not yet full. The second suggestion is that Schrödinger's equation is valid only in microphysics and the measuring apparatus is macroscopic.

If we do not want the dichotomy to return, a smooth transition is to be imagined in a twilight region (e.g. on Ludwig's submacroscopic level [4]) where our experiences are still poor. This was in some sense accepted even by von Neumann himself [5] in accordance with a remark of Wigner. (Another possibility is to rely on hidden variables as done by e.g. Bohm [6], but this solution is becoming ruled out by experiments devised under the influence of Bell's analyses [7].) However, the real question is not whether but how to imagine laws interpolating between micro- and macrophysics. A complete and good formulation would give Schrödinger and Newton limits, and in a Measurement would lead to fast Reduction just after intimate connection between particle and apparatus.

But experimental data leading us to find this interpolation are practically nil. Almost all experimental results show that one of the two limiting behaviours still exists in the particular situation. Since even the proper parameter distinguishing micro- and macrosituations is not uniquely determined, the pure lack of seeing transitional behaviour is hardly enough for further constructive work.

Still, some qualitative features of the future theory can be visualised. The Schrödinger equation gives deterministic changes of Y, a Measurement gives stochastic ones. In an evolution with Measurements at intervals Y becomes stochastic, and then it is not expected to cease to be if Measurement is described by interpolating laws. Then a small body will slightly deviate from deterministic smooth paths in a way resembling Brownian motion. Such a behaviour via Reductions is called "anomalous Brownian motion" [8], [9]. Different kinds of anomalous Brownian motions were predicted in different theories and situations (see e.g. Refs. 9 and 10) but their common property is to be never seen; it is hard to decide if the reason is the undoubted technical difficulty or the irrelevance of the predicting theory. Still, there is a kind of Brownian motion (perhaps anomalous, perhaps not) which is connected with elementary particles, and was at least suggested as candidate for "transitional behaviour". This is the so called "spurious scattering" [11], a deviation from smooth particle trajectories in photographic emulsions without apparent disturbing agent.

The idea that this phenomenon may be of quantum stochastic origin was suggested by L. Jánossy in the '70's, and then some measurements were carried out [12]. But in that time there were hardly any other observations to confront or quantitative models to be checked. Today both kinds of experience have accumulated and now it is worthwhile to compare spurious scattering data to other information.

Chapter 2 briefly lists some ideas about spontaneous wave function reduction. Chapter 3 recapitulates the known phenomenological facts about spurious scattering, and Chapter 4 contains our evaluation of the measurements. Chapters 5 and 6 give the conclusions, first the mathematical and then the physical ones. Appendix A gives some more details about certain models suggested up to now. Finally, Appendices B and C contain some formulae for evaluation.

2."SPONTANEOUS" WAVE PACKET REDUCTION

Since the problem is fundamental and goes back to more than half a century, the literature is huge and standard and we cannot and need not to review it. A substantial number of models has been elaborated, suggested or conjectured, including quantitative, semiquantitative, qualitative and philosophical ones. This paper is mainly devoted to the analysis of experimental data, so it is better to avoid here a review of them. Still, they have to be mentioned, since we are intended to compare later experimental data to theoretical "predictions". So here we give shorthand terms to identify particular classes of models, and something more can be found in App. A.

We mention four different possibilities of mechanisms. The first one will be called self-interaction. The idea is that Y appears in H; an appropriate Hamiltonian then disprefers macroscopic states for a particle. The second mechanism is repeated quantum stochastic multiplication, when the continuous Schrödinger evolution is interrupted from time to time by something else narrowing Y via multiplication by a standard wave form of given width. The third one is influence of stochastic background. This background can be the space-time geometry, fluctuating or smeared by "quantum gravity", or can be anything else, say a field coupled to all particles or only to some ones. Finally, the fourth one is the Berkeleian omniobservant reduction: after discovering QM Bishop Berkeley's slogan Esse est percipi might have been partially reinterpreted, at least in the orthodox QM because perception is a kind of Measurement. So his viewpoint would mean that objects not measured by us are measured time by time by Nature herself. In any of these mechanisms there is a possibility for emergence of new specific parameters, but the parameters may as well originate as byproducts of known mechanisms, as e.g. gravity. Even proper references are relegated to the Appendix.

We certainly do not want to choose among these models, and note that in the lack of one accepted model it is impossible to devise a compact set of decisive experiments. Therefore the meaning and significance of experimental constraints collected up to now are not absolute but scheme-dependent. So now we look for a common conceptual core of different mechanisms and visualize the possible Reduction as follows. Assume that there is a limiting size of microstates; if the size of a particular state of a microobject is smaller, then the Schrödinger evolution is undisturbed, if greater, then Nature regularly restores the limiting width, centering the new Y somewhere in the region where the old one was still substantial. (For the relevant quantity we did have an alternative and now have chosen size.) Then this qualitative picture has two characteristic data: the limiting width s and the repetition time t. Assuming this "mechanism" (suggested by Jánossy [12]) one may then ask: Do we see an effect of such reductions anywhere?

Some predictions of particular models are on the borderline of observational possibilities. E.g. in Károlyházy's model of influence of stochastic background, where the coupling is gravity, a ball of some grams suspended on a rope of 1-10 m length would show an anomalous Brownian motion of amplitude cca. 10^-3 cm [8] but disturbances of environment practically destroy this effect. Similarly, a dumbbell of meter size and cwt mass is expected to perform anomalous Brownian oscillation of some arc seconds, but it could be seen only in a very carefully isolated section of a satellite [10]. And so on. By other words, such minute effects have not been seen up to now, but do not have to have been either. When the mechanism is new or unknown, the free parameters permit an undefined range where the effect would be "expected", and therefore no search is possible. Still, one may accidentally stumble upon a suspected effect.

Jánossy's idea was that the limiting size (separating microscopy and macroscopy) might be somewhere in the range of mm [12]. The reason for this value is clear enough. On one hand, this is the border of visibility, so above it we have our everyday experiences which are macroscopy. On the other hand, higher Balmer lines can be checked in spectroscopy up to, say, the 30^th, they are conform to QM, and for the 30^th one the size of the wave function is some 0.1 mm [13]. As for repetition time t, it simply ought to be short enough not to be observed.

Now, assume for a moment that s_~1 mm and, say, t_~10^-14 - 10^-12 s. (Without any emphasis on it, notice that for this values s_~ct.) Then an elementary particle moving through a photographic emulsion would leave behind a path with measurable anomalous Brownian motion. And the observed spurious scattering (cf. the next Chapter) quite resembles this scenario.

We are well aware that there are observations when the Schrödinger evolution of QM were verified even in this range. Here we mention the electron interferency at cca. 10 mm [14], and successful neutron interference at some cm splitting [15]. (And, of course, genuine macroscopic splitting of photons was long time ago demonstrated [16], but the photon is a par excellence relativistic object, and it is better here to avoid the problems of relativistic QM.) These results impose very serious constraints on any particular quantitative model. However, without careful analysis of the observations where anomalous Brownian motion seems to appear one cannot arrive at sound conclusions. Therefore in the following we deliberately forget about the negative results and will analyze the only (so far) positive observation in itself. But first we note that if spurious scattering were to be ruled out as a Reduction effect, still there would remain ample kinds of possible reduction mechanisms. If, e.g., macroscopy comes from mass, then nothing is expected for an elementary particle outside a measuring apparatus.

3. THE PHENOMENOLOGY OF SPURIOUS SCATTERING

Spurious scattering is a phenomenon of obscure origin observable on tracks in emulsions. For definition and details of analysis see Ref. 11. Recapitulating only the very essence, consider a track without external magnetic and electric fields (as was familiar in some cosmic ray measurements). Then the fine details of the track serve to determine the energy via the evaluation of mean sagitta squares. First the sagittae are defined. The i^th one is built up from the i^th and neighbouring points of the track of coordinates

(x_i-s,Y_i-1); (x_i,Y_i); (x_i+s,Y_i+1)

and then the sagitta D is defined as

D_i≡Y_i+1-2Y_i+Y_i-1 (3.1)

Now, <D²(s)> characterizes the winding of the track. It can be shown that the Coulomb scattering leads to [11]

<D²(s)> ~ cs³ (3.2)

where the Coulomb factor c is energy dependent,

E _~ c^-2, (3.3)

with a prefactor different for different emulsions.

Now, in the realistic case the Coulomb scattering is not clearly separated but appears on a background. The most obvious background is the individual error of measuring Y_i. This produces a nonzero sagitta and is expected to be independent of the cell size s. Then

<D²(s)> ~ a + cs³ (3.4)

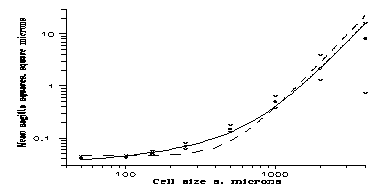
However, experimental data do not follow this law. The deviation will be illustrated on the results of a measurement performed by Jánossy & al. For the original data see Ref. 11; here we have recalculated the fit. In the observation 9 GeV protons penetrated a NIKFI R emulsion stack. The experimental mean sagitta squares with the error bars are given in Fig. 1. We have performed least square fits; the dashed line is of the form (3.4). While the χ² value is not too bad, the points do not follow the curve somewhere in the region 100 mm<s<500 mm. They rather suggest a more complicated law

<D²(s)> ~ a + bs + cs³ (3.5)

This is the solid line, and now the agreement is excellent.

But the new term suggests a third mechanism in addition to simple measurement error and scattering. This effect is called spurious scattering; it was hard to find the real mechanism behind. However, Ref. 11 showed that this term appears if (maybe during the treatment) the emulsion disintegrates into mosaic-like parts and they slip in random directions. Fig. 1 shows that b_~10^-4 mm, which is conform to 0.1-1 mm individual slips at 100-1000 mm intervals.

Postponing the question for a moment whether the new effect exists at all (investigated in the next Chapter), now it is worthwhile to observe that distortion of the emulsion is by no means the only explanation. Just the same order of magnitude is expected for individual displacements of the center of the wave function if the borderline of micro- and macrobehaviour is at cca. 1 mm [13] and if the wave function is repeatedly educed when reaching this size. This was just the essence of Jánossy's suggestion in 1971 [12]. By other words, it is possible that the observed spurious scattering is not a mechanical disintegration and distortion of the emulsion but an anomalous Brownian motion. But this is so only if i) the effect is significant; ii) it does not depend (much) on the characteristic data of the particular emulsion. For deciding this, one must carefully determine the parameter values b in different materials and, maybe, at different energies.

4. THE ACTUAL MEASUREMENTS

Here we analyze and compare the measured values of the spurious scattering parameter b (or its equivalent a³; see later) for protons, in different emulsions and at four different energies, namely at 0.25, 9, 70 and 200 GeVs. The first two energies belong to older measurements, whose results we only reanalyze with special attention on b. At 0.25 GeV E. Fenyves and Éva Gombosi measured one track [11] whose energy was determined from parameter c in the spirit of eq. (3.3). The spurious scattering parameter has been calculated recently by us from the published sagitta squares. The number of measured sagittae N=37; s=500 mm. Hence we get the first column of Table 1. The final results at 9 GeV can be find also in Ref. 11, but in a different form. There <D²(s)> is given at 8 different s values and thence a, b and c can be calculated by a least squares fit. (Ref. 11 gives fits, but they are only partial.) The source does not explicitly give N, but here it is unnecessary for calculating the errors. The emulsion was a NIKFI R stack.

The measurements at 70 and 200 GeVs, in contrast, were originally devised to measure b; and were performed by one of us (Á. H.) as parts of a wider project organized by A. Somogyi in CRIP. The final results of the project are still unpublished, but were deposited at the Jánossy Archive at CRIP. These measurements were performed at emulsion plates irradiated with monoenergetic protons at Serpukhov (70 GeV) and at Batavia (200 GeV). The emulsion types were clearly different in these two cases. The sagittae were measured visually and manually by two microscopes of the same type KORITSKA. The last readable digit was 0.1 mm; however the reliability seemed to be rather 0.5 mm if returning later to the particular point. This inaccuracy seems to have originated from two factors. The first is the width of the track, _~1 mm (determined by the silver-halogenide grains and the treatment), the second was the observable play of the microscope. Only such tracks were used in the analysis which were at least once more reproducible following backwards. (It is worthwhile to mention that the majority of the 70 GeV plates was slightly bent, and the thickness of the emulsion had also some gradient. This hindered the measurement, and reduced the number of appropriate tracks by cca. 40%.) The elementary cell size was 0.5 mm, and the number of processed sagittae was cca. 3000 at 70 GeV, and cca. 2000 at 200 GeV. The mathematical method of the analysis was the same as given in Ref. 11, and will be briefly recapitulated in App. B. At this place we only mention that the global curvature of tracks (and plates, if so) were removed by a fit of prescribed way via 2^nd order Legendre polynomials. The final results of the analysis are given in Columns 3 and 4 of Table 1.

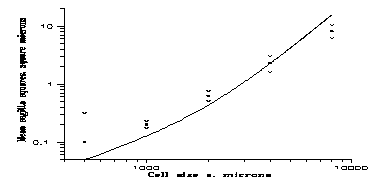
In addition, at 200 GeV the mean sagitta squares were measured at 4 other s values too, namely at 1, 2, 4 and 8 mm's, obviously with less statistics. This, in principle, enables us to determine the parameters in an alternative way too (the one followed at 9 GeV). This would be dangerous, having only 5 points to determine 3 parameters, hovever <D²(s)> is given in Fig. 2 for checking the obtained parameters. We calculate a, b and c first from the mean sagitta squares of the 500 mm measurements (the best statistics with N=1885), and then compare the different sides of eq. (3.5).

When interpreting the results, sometimes the parameters a⁽ⁱ⁾ will be used as synonyms of a, b and c. For clarity we give here the connections, although the mathematical details have been relegated to App. B:

a = 6a⁽²⁾

b = a⁽³⁾/s (4.1)

c = 4a⁽¹⁾/s³

E, GeV	0.25	9	70	200
a, µm²	-4.97*10^-2	3.33*10^-2	2.94*10^-1	-4.47*10^-3
b, µm	1.31*10^-4	1.33*10^-4	2.16*10^-5	1.02*10^-4
c, µm^-1	2.54*10^-10	2.41*10^-10	1.12*10^-10	2.92*10^-11
s^aa, µm⁴	3.60*10^-3	1.37*10^-5	1.17*10^-4	2.78*10^-5
s^ab, µm³	-3.96*10^-6	-1.09*10^-7	-6.71*10^-8	-2.39*10^-8
s^ac, µm	2.79*10^-12	7.87*10^-14	2.40*10^-14	3.99*10^-15
s^bb, µm²	4.75*10^-9	1.21*10^-9	5.48*10^-11	2.50*10^-11
s^bc, µm⁰	-3.66*10^-15	-9.95*10^-16	-2.27*10^-17	-4.51*10^-18
s^cc, µm²	8.29*10^-21	4.97*10^-21	2.40*10^-23	4.38*10^-24
N	37	?	~ 3000	1885

Table 1: The parameters of eq. (3.5) and their error matrix from the mean sagitta squares

5. CONCLUSIONS: MATHEMATICAL

In this Chapter we completely ignore the physical meaning of the parameters, and concentrate on the question what is the value of the parameter b and whether it significantly differs from 0 or not.

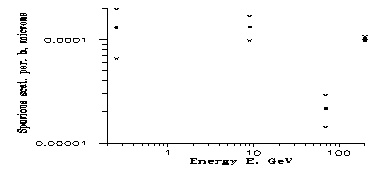
For first orientation one can compare b to √s^bb . Then b differs from 0 on (cca.) 2s level at 0.25 GeV, on 3s at 9 and 70 GeVs and on 20s at 200 GeV. So it would seem that the existence of the effect has been established without doubts (with the necessity of new measurements of larger statistics at lower energies) and we can look at the values and energy dependence of b. This is indeed done in Fig. 3, but observe the deep depression at 70 GeV, which is strange in the best case.

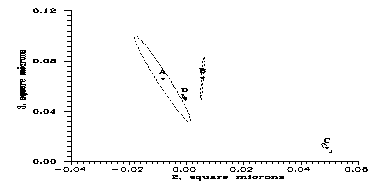
Now, some anomaly thus detected, we turn to the error matrices. Table 1 shows that da and db are very strongly correlated at any energy. Since correlations with dc is not so substantial, one can visualize the situation in a 2 dimensional parameter subspace as done in Fig. 4 (for technical reasons for a⁽²⁾ and a⁽³⁾). Then it is characteristic to have a "diagonal" error ellipse, but it is also striking to have negative a values (i.e. background noise) at some energies. From these two facts one directly arrives at the conclusion that at least some part of b must be an artefact, and should be considered as belonging to a. A very remote analogy is the experience that sometimes in such measurements the error of individual sagittae increased along the track [17].

This is quite possible. One might, e.g., argue as follows. The width of the track is cca. 1 mm. If its center is not correctly found, there is, say, 0.5 mm random walk in each 500 mm step. However, consider the following facts. First, we used two very different ways of analysing the data; in one of them the step length varied between 50 and 4000 mm's and still the linearity remained in the final results. Both methods gave b values roughly similar (except for 70 GeV) and quite significantly nonzero; and both methods gave strong correlation between da and db. So the b values cannot be simply false consequences of systematic errors of a particular method. (Some systematic errors would be quite possible for, e.g., a sagitta distribution essentially non-Gaussian.) Second, as seen in Fig. 4, even with this strong correlation the error ellipses are far from the a⁽³⁾ axis (b=0). Therefore here we can conclude that systematic errors are quite possible, can be conjectured from the anomaly of errors, and this feature should be better understood, nevertheless spurious scattering seems to exist and the order of magnitude of b is 10^-4 mm. We must confess that the substantially different value at 70 GeV is not yet explained.

Still remains the question if the new term is really linear in s. Ref. 11 notes that various fits are possible and have been found in different measurements between first and third powers. (This would indicate different b's in different measurements too, but we got practically the same value in 3 measurements, and note that they were performed by different groups, in different emulsions, using different apparatuses and extended over more than a decade.) One could directly compare bs and bs² fits for 9 GeV. However the statistics is not very good, and until no clear theoretical prediction exists, the discussion of the exponent is almost pointless.

6. CONCLUSIONS: PHYSICAL

Now, let us accept, according to the previous Chapter, that the spurious scattering exists and was observed in the mentioned emulsions. Then, what is the physical meaning of the result?

Consider first the "conventional" explanation, tentatively mentioned in Ref. 11; that is the mosaic-like disintegration and minute slips in the emulsion. This is obviously possible; however then the spurious scattering parameter would depend on the type of emulsion and on the details of treatment, while would be fairly independent of the particle and its energy. We will once more return to this point; however in the present measurement the parameter b does not seem to depend either on energy or on the actual type of emulsion (except for both possibilities the strange 70 GeV case, which was just the case when the emulsion was in the worst shape, so it would be hard to imagine that disintegrations and slips would have been minimal there). In order to rule out this possibility detailed materials science investigations would be needed for the behaviour of emulsions, not available for us. We note that Jánossy himself dispreferred his own earlier conventional explanation at the middle of the '70's [18].

The alternative possibility is that a "quantum stochastic" effect of any kind is seen. Now we are going to compare the results with the (rather qualitative) predictions of the four different reduction models mentioned in Chap. 2 and listed in more details in App. A.

Self-interaction.

As mentioned in App. A, in itself it does not lead to Reduction, so does not lead to anomalous Brownian motion either.

Repeated quantum stochastic multiplication.

At first, one is tempted to try with s_~10^-4 cm and t_~10^-12 s, to get the observed random walk. However, below we show that in this mechanism the above parameter values do not lead to 1 m random walk in each 100 mm's.

The mechanism is a free expansion for time t and then multiplication by a Gaussian of width s. However, during the prehistory of the proton, a large number of such cycles has happened, therefore now, when passing the emulsion, the cycles must be stationary, i.e. all cycles must start with the same width. Ref. 19 gives the evolution of a Gaussian wave packet through cycles. With the above parameters the free Schrödinger expansion is relatively very short, as characterized by the dimensionless parameter

ε ≡ th/ms² _~ 10^-9 << 1 (6.1)

Then, substituting into the formulae of Ref. 19 one gets that in the stationary case

<(q-<q>)²> ~ √ε s²

<(p-<p>)²> ~ h²/2s²√ε (6.2)

<(q-<q>)(p-<p>)> ~ h/2

up to lowest terms in ε, as well before as after Reduction.

Then a simple but tedious calculation gives the random walk obtained from jumps located in the region {<(q-<q>)²>}^½ , with the result

<D²(s)> ~ 4(h/p)s + (1/2s²)(h/p)²s² (6.3)

where p is the original momentum in x direction. (There is a trivial constant term too from the stationary width of Y too, which goes to the noise. for further terms see Ref. 22, but we note that here we are not in the limit treated there, and the next cubic term would mimic Coulomb scattering anyway.) So both a linear and a quadratic spurious scattering is obtained. However the amplitude is too small. With the above s_~10^-4 cm for a 70 GeV proton at s=100 mm the sagitta square is cca. 10^-17 cm², 8 orders of magnitude below the experimental value. Observe that this s value is the absolute limit of possibilities, therefore one can conclude that the Ghirardi-Rimini-Weber mechanism cannot explain the observed spurious scattering at any possible parameter value. In addition, the first, leading term does not even contain any new parameter.

The reason is explained in details in App. A; briefly the short time interval t needed for any emulsion effect prohibits expansion, then repeated multiplication makes Y too narrow and the random walk substantially decreases.

Influence of stochastic background.

If that background is stochastic gravity then no observable spurious scattering appears. Namely, elementary particle masses are so low that gravity breaks down the superposition only in astronomical times. (A rough estimation based on Refs. 8 and 9 gives 10⁵³ s.) If the background is a so far unknown stochastic field, any result can be obtained, of course.

Berkeleian omniobservant reduction

This is the only mechanism where any hope has remained. However no definite model exists up to now. So we can only say that the measured spurious scattering data may be compatible with such a reduction mechanism. Numerical calculation is unnecessary here; Ref. 11 gave the formulae for a random walk, which remain valid, mutatis mutandis, when the random walk is caused by a Measurement independent of us. With a limiting width, when Reduction becomes effective, Σ_~0.1 mm, and with a repetition time t_~10^-12 s, b_~10^-4 mm, as measured. However now is the proper time to note that electron and neutron splitting experiments above mm range strongly oppose such an explanation, and this is just the reason to emphasize that spurious scattering measurements would deserve more attention.

There remains an obscure possibility. It is not yet ruled out that the observed effect is a quantum stochastic one, but not at the particle but in the emulsion. Namely, in an emulsion there are silver-halogenide grains of the size of µ 1 mm. Now, Ref. 8 evaluated, in the gravitational stochastic background model, a situation when a particle enters the Wilson chamber through two slits. Then the result is that first two latent tracks of microscopic droplets are formed, but later, when the mass grows sufficiently, the superposition breaks down and only one of the tracks survive.

Now in our case the size and mass of grains are in the order of the "submacroscopic" level, so some transient behaviour can be expected. Gravitational stochastic background models (e.g. Refs. 8 and 9) roughly give t_~10⁺³ - 10^-12 s when R changes in the range 0.1-1 mm. Therefore in this range the wanted "repetition time" may appear, while the individual step amplitude seems to be just the individual grain size.

Here no more definite statement will be done, because of i) the difficulty of the actual calculation in a disordered solid state; ii) practical considerations. To explain the second statement, observe that if the quantum stochastic effect depends on the internal structure of the emulsion, then the effect is hardly separable from the previously suggested internal disintegration of the emulsion. Unfortunately any other track detectation method not using awkward materials, as e.g. streamer chamber, has too low resolution to detect the effect (being at 0.1-1 mm².)

So our conclusion here cannot be more definite than: it seems that spurious scattering exists; no serious depence on emulsions is seen, therefore the effect may be of quantum stochastic origin, but no qualitative model is known for explaining the data. We think that a methodical survey using different emulsions with monoenergetic tracks at a higher statistics (and also, identical emulsions with tracks of different energies and/or particles) might contribute to the better understanding of the "measurement problem" of Quantum Mechanics, in the worst case by ruling out counterevidences.

ACKNOWLEDGEMENTS

The authors would like to thank Dr. L. Diósi for illuminating discussions on various reduction mechanisms. One of them (Á. H.) acknowledges the organizing activity and valuable personal help of Prof. A. Somogyi, and also thanks the late Prof. L. Jánossy for suggesting the topics and for illuminating discussions.

APPENDIX A: ON SOME REDUCTION MODELS

Here we want to mention only some representatives of classes of suggested mechanisms, deliberately confining ourselves to the nonrelativistic limit, to avoid the appearance of quantities of such exotic values as e.g. Planck length.

For the parameter distinguishing micro- and macrosystems the two obvious candidates are size R and mass M. However from dimensional considerations it may quite well be M³R. Namely, it is the only mass-size combination whose dimension can be produced from the two truly fundamental constants h and G. (We have ignored relativity so c cannot appear.)

Self-interaction:

The first kind of ideas can be illustrated on an early model of Jánossy from 1952 [13]. To avoid the macroscopic splitting of an electron he introduced a term, growing with wave packet size, into the Hamiltonian. This is a self-interaction, and Ref. 13 gave a specific form for it: H=H_o+O, where

_∞

O ~ ∫P(x-x')|Y(x')|²dx' (A.1)

^-∞

and P(x) is a monotonously increasing function of |x| of appropriate form. In such self-interactions the new parameter setting the borderline between micro- and macrosystems has the dimension erg/cmⁿ, n depending on the details of the potential. A different variant is when the self-interaction is gravity [20], [21]; then there is no room for new free parameter. The problem with such ideas is twofold: first, a photon can be split up for genuine macroscopic sizes [13], but, of course, a photon never has any nonrelativistic limit. Second, such self-interaction prevents macroscopic expansion but does not give automatically Reduction.

Repeated quantum stochastic multiplication

The second kind of ideas is the postulation of a fundamental "quantum stochastic" reduction mechanism. The most versatile one has been suggested by Ghirardi, Rimini and Weber [19].

Roughly speaking, there is a Schrödinger evolution interrupted at intervals by "something else". This "else" is postulated to be a multiplication by a given function

Y(x) → (norm)*Y(x)*exp{-(x-X)²/4s²} (A.2)

where s is a constant parameter and the "center" X is a stochastic variable with the distribution

p(X) = Y^*(X)Y(X) (A.3)

The multiplication is triggered by the passing time; the interval is also a stochastic variable with some distribution and an average t.

The new parameters s and t may be fundamental constants but may as well depend on, say, mass. Ref. 19 suggests parameter values at which elementary particles are practically unaffected while macroobjects have no free Schrödinger evolution for any observable time. However, if something were to be seen for particles, it would be natural to look for new parameter values. Obviously for elementary particles s>10^-7 cm (not to disturb atomic orbits) and t>10^-14 s (not to disturb light emission).

There is a continuous limit (t → 0, s →∞, τσ²=finite) when the two competing evolutions are simultaneous. This limit can be obtained from the next mechanism too, with stochastic gravity [22]. Then the remaining parameter is not free but

τσ² _~ (hR³/GM²) (A.4)

Influence of stochastic background

A third possibility is that a stochastic "field" influences the wave functions via coupling, and then they become stochastic too. If the "field" or the coupling is such that it influences macrosystems very strongly, then it may destroy macroscopic superpositions. Károlyházy postulates stochastic fluctuations of the space-time geometry as agent [8], [23].

Assume that the space-time geometry is nearly Minkowskian but not sharp ("Quantum Gravity"). Then

g_ik(ß)=h_ik+g_ik(ß); |g_ik|<<1 (A.5)

where _ß labels the "actual" manifold. Károlyházy visualizes the fluctuations as "gravitational waves" with a power spectrum, where the parameters

<|c_k|²> _~ l_Pl^4/3k^-5/3 (A.6)

come from some combined uncertainty relations (for a review see Ref. 24). Since Y evolves on a stochastic space-time, its phase becomes stochastic, and Reduction is postulated when the stochastic uncertainty of phase reaches π. (No more interference, no more superposition.) This model is conceptually relativistic, but has a limit for slow particles.

A similar model can be based on the observation that QM prevents the sharp definition of the Newton potential [25]. Completely ignoring relativity one could get an "uncertainty relation" for the acceleration g:

<(dg)²> _~ (hG/VT) (A.7)

It can be interpreted as a stochastic component of the Newton potential F:

<F_st(x,t)F_st(x',t')>_~hG|x-x'|^-1d(t-t') (A.8)

and the effect of this stochastic potential may lead to Reduction [26]. Ref. 24 rediscussed the uncertainty relations used in Ref. 8 and has arrived at a nearly Minkowskian space-time with the Newtonian limit (A.8). Of course, any of the various "Quantum Gravity" models could be evaluated for wave packet reduction.

If the coupling is gravitational according to Occam's razor, there is no free parameter. In addition, then practically only macroscopic (and "submacroscopic") objects are affected, and the borderline is [9], [25]

M³R _~ h²/G (A.9)

which, for earthly densities, is located at R_~10^-5 cm, M_~10^-14 g. This is an average colloidal grain.

If needs be, one could postulate any new stochastic field too, directly unobservable but coupled to known particles by handmade coupling constants. Analogous tasks are today accepted in GUT cosmologies (for review see Ref. 27), but this will not be done here.

Berkeleian omniobservant reduction

If Esse est percipi [28], still remains, what is percipio. According to orthodox QM, percipio~metior, pondero. If so, in our age the Bishop would say that a body not measured by any of us is still measured by God, and therefore His omniobservancy keeps the states only microscopically smeared. The idea is similar to the repeated quantum stochastic multiplication, but not at all the same. To see this, consider the mechanism (A.2-3) with parameters

t << s²m/h (A.10)

Then there is no time for Y to substantially expand between multiplications, therefore for a longer time

<(x-<x>)²> _~ s²(t/t) (A.11)

The wave fuction is continuously shrinking and after some time drops below even the well checked atomic sizes.

In contrast, repeated Measurements only restore again and again some limiting size. The simplest example is as follows. Assume that the system has its own linear H, but there is another operator, say Jánossy's nonlinear Hamiltonian H+O [13] giving too high energies above a limiting size Σ_~1 mm, and Nature applies it on Y at t intervals. Then for a bound microscopical system practically nothing happens, because the effect of O is negligible compared to that of H. For an unbound particle nothing happens until the expanding size is below Σ. When the size enters that range, however, then each Measurement of Nature substitutes Y with one of width ð centered somewhere in the region where Y before Measurement still was substantial. Then further expansion stops, and there appears a "random walk" with Σ steps at t intervals even if uneq. (A.10) holds. So in this limit this mechanism substantially differ from quantum stochastic multiplication.

APPENDIX B: FORMULAE FOR EVALUATING THE SAGITTAE

The whole method is given in Ref. 11. For some details see also Refs. 29 and 30. Here we give only the formulae needed to understand the results.

The individual sagitta D_i(s) is defined in eq. (3.1); the x axis is the average of the track. First one has to eliminate the global curvatures. It is done by

∑_i(D_i(s)-∑_αg_αP_α(x_i))²=min. (B.1)

where P_α is the A^th Legendre polynomial, and then

D_i(s)-∑_αg_αP_α(x_i) → D_i(s) (B.2)

Then eq. (3.5) in a fit leads to

α⁽¹⁾=(2d⁽⁰⁾-3d⁽¹⁾-d⁽²⁾)/168

α⁽²⁾=(16d⁽⁰⁾-10d⁽¹⁾+d⁽²⁾)/42 (B.3)

α⁽³⁾=(-8d⁽⁰⁾+9d⁽¹⁾-d⁽²⁾)/12

with

d^(l)=∑₁^ND_i^(l)2

D_i^(l)≡Y_i+q-2Y_i+Y_i-q (B.4)

q≡2^l

The parameters α can be regarded as measured values of the quantities a, b and c via the relations (4.1). The fundamental assumption of the method is that the "noise" as well as both "scattering" processes have Gaussian distributions.

Ref. 11 gives the error matrix as follows. Define first x and y as

x≡α⁽²⁾/α⁽¹⁾; y≡α⁽³⁾/α⁽¹⁾ (B.5)

Then form the matrix

q⁺_ik=(1/π)∫f_ik(z)W^-2(x,y,z)dz

0 (B.6)

W ≡ [2+2x+y+(1-4x-y)cosz+2xcos²z]

f₁₁ = (2+cos z)²

f₁₂ = 2(2+cos z)(1-cos z)²

f₁₃ = (2+cos z)(1-cos z)

f₂₂ = 4(1-cos z)⁴

f₂₃ = 2 (1-cos z)³

f₃₃ = (1-cos z)²

Hence one can get the matrix Q:

(Q^-1)_ik = (N/2α⁽¹⁾²)q⁺_ik(x,y) (B.7)

where N is the number of sagittae. And then

<δα⁽ⁱ⁾δα^(k)> = Q^ik (B.8)

We have followed this method, i.e. at 0.25, 70 and 200 GeVs the errors are calculated in this way, not directly from the (uncontrollably correlated) errors of d⁽ⁱ⁾. However very non-Gaussian distributions would invalidate the method leading to an explicit inconsistency between the above error matrix and the one obtained via least squares.

APPENDIX C: ON THE MEANING OF THE ERROR MATRIX

Consider a parameter vector with an actual measured value pⁱ and an error matrix g^ik. In the parameter space g^ik defines a natural metric [31], [32], so two measured values p₁ⁱ and p₂ⁱ are not significally different if they can be connected with a path on which

S(1,2) ≈ {∫g_ik(p)dpⁱdp^k}^½ (C.1)

is not above 2 or 3. This was the criterion when interpreting Fig. 4.

REFERENCES

[1] H. Everett, Rev. Mod. Phys. 29, 454 (1957)

[2] E. Schrödinger, Naturwissenschaften 23, 844 (1935)

[3] E. P. Wigner in: The Scientist Speculates. Ed. I. J. Good, W. Heinemann, London, 1961

[4] G. Ludwig, Werner Heisenberg und die Physik unserer Zeit, Braunschweig, 1961

[5] J. von Neumann, Matematische Grundlagen der Quantenmechanik. Springer, Berlin, 1932

[6] D. Bohm, Phys. Rev. 85, 166 (1952)

[7] J. S. Bell, Rev. Mod. Phys. 38, 447 (1966)

[8] F. Károlyházy, Magy. Fiz. Foly. 22, 23 (1974) (in Hungarian)

[9] F. Károlyházy, A. Frenkel, B. Lukács, in: Physics as Natural Philosophy, eds. A. Shimony and H. Feshbach, MIT Press, Cambridge Mass. 1972, p. 204

[10] F. Károlyházy, A. Frenkel, B. Lukács, in: Quantum Concepts in Space and Time, eds. R. Penrose and C. J. Isham, Clarendon Press, Oxford, 1986, p. 109

[11] L. Jánossy, Theory and Practice of the Evaluation of Measurements. Clarendon Press, Oxford, 1965

[12] L. Jánossy, lecture given at his 60^th birthday in CRIP, May 1971; unpublished. See also the CRIP Yearbooks for years 1971-1975

[13] L. Jánossy, Acta Phys. Hung. 1, 423 (1952)

[14] J. Wodilla and H. Schwartz, Am. J. Phys. 39, 111 (1971)

[15] C. G. Shull & al., Phys. Rev. Lett. 44, 765 (1980)

[16] L. Jánossy and Zs. Náray, Nuovo Cim. Suppl. 9, 588 (1958)

[17] G. Jancsó, private communication

[18] L. Jánossy, private communication

[19] G. C. Ghirardi, A. Rimini and T. Weber, Phys. Rev. D34, 470 (1986)

[20] I. Bialinicki-Birula and J. Mycielski, Ann. Phys. 100, 62 (1976)

[21] L. Diósi, A105, 199 (1984)

[22] L. Diósi, Phys. Rev. A40, 1165 (1989)

[23] F. Károlyházy, Nuovo Cim. 42, 390 (1966)

[24] L. Diósi and B. Lukács, Phys. Lett. 142A, 331 (1989)

[25] L. Diósi and B. Lukács, Annln. Phys. 44, 488 (1987)

[26] L. Diósi, Phys. Lett. A120, 377 (1987)

[27] A. D. Linde, Rep. Prog. Phys. 47, 925 (1984)

[28] G. Berkeley, Treatise on the Principles of Human Knowledge. London, 1710

[29] L. Jánossy, A. Lee and P. Rózsa, Publ. of the Math. Inst. of the Hung. Acad. Sci. 6, (1961), Ser. B.

[30] L. Jánossy and P. Rózsa, Nuovo Cim. 20, 817 (1961)

[31] J. Weinberg, Gen. Rel. Grav. 7, 135 (1976)

[32] L. Diósi et al., Phys. Rev. A29, 3343 (1984)

Figure Captions

Fig. 1: Mean sagitta square <D²> vs. cell size s for a 9 GeV proton track. Heavy dots and crosses: measured values and errors. Continuous line: best fit with formula (3.5). Dashed line: best fit without the spurious

scattering term, eq. (3.4). Details in the text.

Figure Captions

Fig. 2: Mean sagitta square <D²> vs cell size s for 23 tracks. Continuous line: formula (3.5) with coefficients

obtained via the method of App. A (Table 1). The curve fits well to <D²(s)>, so two different methods give compatible results.

Figure Captions

Fig. 3: Spurious scattering parameter b vs. energy E in the four evaluated case. Observe that at 3 energies in

different emulsions b is essentially the same. The depression at 70 GeV is still without explanation.

Figure Captions

Fig. 4: Measured parameter values (α²,α³) with the error ellipses. Dotted, A: 0.25 GeV; short dash, B: 9 GeV; long dash, C: 70 GeV; continuous line, D: 200 GeV. More details in the text.

My HomePage, with some other studies, if you are curious.