ON THE THERMODYNAMICS OF METEORITES AND PARENT BODIES II: PORTALES VALLEY AND THE BORDERLINE OF CHONDRITES AND ACHONDRITES BETWEEN MEMBERS OF THE H+IIE CLAN
Sz. Bérczi1, Ágnes Holba2 & B. Lukács2
1 Eötvös University, Cosmic Mat. Sp. Res. Gr. H-1117 Budapest, Pázmány P. s. 1/a. Hungary
2 CRIP RMKI H-1525 Budapest 114. Pf. 49. Hungary
ABSTRACT
We place the new Portales Valley metal-veined H6 chondrite among the transitional H chondrites between metamorphic grade 6 and the more evolved and differentiated H and IIE related achondrites and irons.
INTRODUCTION
Among the abstracts of the 30th Lunar and Planetary Science Conference (since 29th January, 1999, on the Internet address http://cass.jsc.nasa.gov/meetings/LPSC99/) in session 71. one finds exciting reports about a new H chondrite, Portales Valley, which contains metallic veins. Working on meteorite parent body evolution during the last 5 years we became encouraged to carry out theoretical estimations and statistical comparisons (using NIPR Antarctic Meteorite Dataset, Yanai & Kojima, 1995) about the role of the new meteorite. Thus the present paper is the continuation of Bérczi, Holba & Lukács (1996) which, consequently, will be cited henceforth as Part I. We are continuing Part I to the direction of the (mainly high-temperature) end of chondritic evolution and the merging into achondrites.
Thermal metamorphism forms gradual transitional mineral assemblages (and compositions) between chondritic, achondritic and differentiated meteorites. After classification of chondritic metamorphism (van Schmus, Wood, 1967) examples for transitional textures between chondritic to achondritic ones are slowly but continuously accumulating. They are in focus of research in the last 20 years. There are four such pioneering recognitions for chondrite related irons. The transitional meteorites are Rose City, Netschaevo, Watson, Techado and the latest the Portales Valley veined H6 chondrite. They can be arranged in a sequence according to their oxidized iron content and the degree of melting of their iron.
Many of our earlier works (and one of our reports on 30th LPSC, No. 1014) deal with thermal evolution of chondritic meteorites and characterizes this process by projecting Fe-bearing compounds onto the Urey-Craig field. On this field the metamorphic types of E, H, L, LL and C chondrite groups form thermal evolution paths of their chondritic meteorite parent bodies (Bérczi, Holba, Lukács, 1995, Lukács, Bérczi, 1996); in the suggested R, G and K groups we still are unable to see evolutionary trends. We found that between E and H groups primitive achondrites occupy a special role. Over this region in E chondrites reduction at petrologic type 4 run toward more reduced stages. For H chondrites more and more reoxidized states follow, see Fig. 12 of Part I. (We described these events by parameters of C/H2O ratio which showed the redox competition of reducing C and oxidising H2O for Fe, Lukács, Bérczi, 1996.)
THE SEQUENCE OF CHONDRITES
The great variety of chondrites probably have some internal structure. A simple relationship is if the letter (E, H, L. LL and C) shows the initial condition, while the number (the petrologic type, henceforth PT, from 1 to 7) does the thermodynamic evolution from the initial condition. Fig. 16 of Part 1 shows the simplest such evolutionary scheme for the 30 samples of the remarkable NIPR Antarctic Thin Section Set; there the idea was that evolution had gone along the lines from left to right. This is of course a hypothesis; according to new results oversimplified at least in one point which will be discussed later. However the most fundamental point of that scheme still seems valid: the "foliated" structure of the "thermodynamic state space" of the meteorites. "Horizontally" there may be genetic connections, but not vertically.
This "foliation" can be checked. Initial conditions can be seen on non-volatiles; a statement made more definite immediately. For graphs see Bérczi, Holba & Lukács (1995). Also, some results are displayed (Lukács, Holba & Bérczi, 1999, LPSC 30, #1337). So far we checked in details the Mg and Fe contents, and also some abundances which do not seem reversible, of which here we mention FeS and C. Hence we think that the following relations are established. We use abundantly the data of the NIPR Antarctic Meteorite Catalog (Yanai & Kojima, 1995), which is a large, homogeneous body of data. Later reclassifications of individual meteorites occasionally have occurred and may happen in the future, but for definiteness' sake are ignored here. In some points, and definitely for carbon data, we also use Jarosewich's data (Jarosewich, 1990).
Among E chondrites PT 3-6 are known so far. Subgroups EH and EL are more or less consequently discriminated in the latest years but the group is rare and so the statistics is not good. For the whole E group Mg/Si is significantly lower than for ordinary chondrites (Lukács, Bérczi, 1996), FeS and C is more abundant than in other groups except C. Total Fe is reported to decline from E5 (Mason, 1962), but our opinion is that this is iron loss by dropping out, and so no evidence against genetic connection between early and late E's, we will return to this point later. E achondrites seem direct continuation of the evolution with total metallic (and sulfide) Fe loss. It is worthwhile to repeat Mason's (1962) note that chondrules do not seem in E6's, which is against the van Schmus-Wood (1967) convention.
There are the following PT's established so far in the H group: 3, 3-4, 4, 4-5, 5, 5-6, 6. We are now convinced that H3-4's of the NIPR Catalog originated from initial conditions alien from either the H or the E group. Their iron content is significantly higher than in the H group; it would fit into the E group, but H3-4's are poorer in FeS than even E4's. The origin of H3-4's is still obscure. The transitional types 4-5 and 5-6 do not deviate from the H trend (see Fig. 12 of Part I), and so they can be genuine H's. The H achondrites are not yet known. The H group is characterised by "average" Mg/Si and "high" Fe/Si.
L's are known as 3, 4, 5, 5-6, 6 and 6-7. L5-6's do not deviate from the trend, but the redox processes were simpler without this rare subgroup. If the only L6-7 of the NIPR Catalog is genuine L, then it shows final Fe° loss (as E5&6, see this later in details). The group has average Mg/Si and low Fe/Si. (Hypersthene achondrite of Mason, 1962 was later named diogenite. But one extraordinary sample: Yamato 790126 was classified to L6, (Yanai, Kojima, 1987), however, it did not contain chondrules so may be L7, and this may be the link to L achondrites.)
LL's are found in PT 3, 4, 5, 6 and 7. All of them fit into the trend, with Fe° loss in LL7. LL's are characterised by average Mg/Si and low Fe/Si, just as L's, but their Fe/Si is slightly lower, and Fe°/Si is significantly lower. (Real LL achondrite does not exists. On the basis of their FeO/ Fe° ratio chassignite and eucrite was considered as LL achondrite.)
The C group is recently becoming a supergroup, distinguished by second letters as CI (only 1), CM (2, and according to Zolensky & al., 1), CR (mainly 2, but according to Zolensky & al. 1997, in PT 1 too, at least mosaically), CO (only 3), CV (generally 3, but Kaba is maybe 2, and Coolidge 4), CK (4&5?) and so on. The systematics is obviously in change recently. Anyway, the trend seems to be a partial reduction until PT3, and then reoxidation (Lukács, Bérczi, 1997). The C (super)group is characterised by high Mg/Si and high Fe/Si. The ureilites share the high Mg/Si abundance. While their Fe/Si is too low, so they directly cannot be C achondrites, at least they remind us them.
Now, the only possibility for "vertical" transitions is L <‑> LL, and even that is not probable, except misclassifications. Between any other 2 groups, as it is shown, conserved ratios differ, so "superselection" rules prohibit transitions. On the other hand, with the above mentioned exception of "H3-4" within a group all PT's seem accessible by i) aqueous alteration (see later), ii) by redox processes (for which agents C and H2O are present, iii) by sulphide loss (details obscure) or iv) by Fe° loss in terminal stages (later).
These genetic chains, then, seem more or less well-founded, and even connect chondrites to ("primitive", i.e. undifferentiated) achondrites. However the two ends of chondritic chains need discussion. In Part I we took the simplest picture when all chains start in PT 1, however it seems that the situation is not so simple. We remark that the following 2, short, Sections have nothing to do with Portales Valley; however they are incorporated here for completeness' sake. They deserve more detailed treatment in another paper.
THE PRIMITIVE CHONDRITE
If one wants to read PT's as the direction of Time's Arrow, then the evolution of chondrites start from no chondrule (see, with some mental reservation, Part I). The picture is by no means impossible, see e.g. Mason's idea (1962) for olivine & pyroxene chondrules formed from serpentine via heating, H2O loss &c. In addition, compositions of Orgueil, Ivuna and Y-82162 can be hardly derived from C2's (e.g. because of high FeS). Still, present observations (e.g. Zolensky & al., 1997; McSween, 1979) seem to prove the inverse route (see the next Chapter).
For the C chondrites of the NIPR Catalog the "primitive" C seems to be somewhere among C2's. However the general feeling is that the groups E, H, L and LL start in PT 3.
Now, this may be a simple convention. E. g. consider Hutchison Alexander & Barbers suggestions (1987) that "LL 3"'s Semarkona and Bishunpur should be reclassified as LL 2.
The problem is twofold. First, a meteorite is an open system, so we do not have such a sure Time's Arrow as specific entropy for closed systems, moreover we must admit that this problem is not finally solved in Thermodynamics. Second, in the van Schmus-Wood nomenclature both PT 2 and PT 3 are characterised by "sharp chondrules". The 2 PT's are discriminated via H2O and C contents, which, however, cannot be used when one compares chondrites of different initial conditions.
Still, we can conjecture the evolutionary relations by probability arguments. It is much more probable to almost any process to destroy sharpness of chondrules than produce; loss of volatiles as H2O and C could be more frequent than gain; and in most meteorites FeS is the only major S source, so FeS cannot grow.
Hence one can say that an LL 2 is something more primitive than LL 3 if its chondrules are sharp too but the H2O, C and FeS contents are "too high". Now, the suggested LL 2's Semarkona and Bishunpur (Hutchison, Alexander & Barber, 1987) have much higher than average C content, while H2O and FeS are at least too among the highest (Jarosewich, 1990). In one of our 30th LPSC poster (Bérczi, Holba & Lukács, 1999, #1275) this suggestion is accepted and the arising carbon trend is quite acceptable. On the same basis we suggest Sharps H3 (Jarosewich, 1990) to be reclassified as H2.
Fig. 1 shows a three-colour map for Fetot, Feox, H2O and C for chondrite types (Bérczi, Holba & Lukács, 1999, #1275) in the spirit of this Chapter.
Fig. 1: NIPR Catalog chondrites
red=reduced Fe, green=carbon, blue=water
If so, then the primitive or initial chondritic state is in PT 2 or between PT 2 and 3.
RETROGRADE (AQUAEOUS) ALTERATIONS
Now, from the primitive state, according to the circumstances the evolution may go into 2 directions. In dry conditions diffusion starts. This was treated in Part 1 and will be again detailed in the next Section. However in very wet environment aquaeous processes can start. Zolensky & al. (1997) demonstrated the "retrograde" process CM2‑>CM1 (and, virtually, CR2‑>CR1 too), and Kaba is at least an example when it is doubtful if the petrologic class is 2, 3 or 4 (e.g. the chondrules are anomalous).
Here we note only that there are thermodynamic similarities between the "direct" (diffusion) and "retrograde" (aquaeous) evolutions. Preparing an initial stage of sharp chondrules and large gradients in chemical potentials (for ordinaries often regarded as PT 3.0), then both processes simultaneously unsharpen the chondrules and decrease the gradients of chemical potentials. To see Time's Arrow detailed differences should be observed.
Now we shift our attention to direct evolution and also recapitulate some statements from Part I.
DIFFUSION
Obviously the genesis of parent bodies was complicated and observation is impossible. However diffusion must have been present, and it seems that the main facts of direct chondritic evolution can be interpreted via it.
Assume an initial stage of sharp chondrules and large chemical gradients in a more or less olivine-pyroxene assemblage at the formation of asteroid-sized parent bodies; if it happened just after the primordial crystallization then short-lived nuclei as Al26 (t1/2=7.4*105 y) or Pt244 (t1/2=7.6*107 y) could still produce a high temperature. If one does not believe in this, he may rely on heat from the gravitational accretion.
The simplest model is a constant temperature To for a time to~t1/2 and then a negligible equilibrium temperature. Then diffusion establishes homogeneity on a length
lD ~ (Doto)1/2 (1a)
Do = D(To) (1b)
Let the primordial chondrule size be ro. This quantity varies from group to group, but now for orientation we take ro~0.3 cm. One can improve the presentation by substituting better values.
Via only diffusion, a chondrule border is sharp if lo<<ro (and then PT is 2 or 3), clear if lo~ro (PT 4&5), obscure if lo>ro (PT 6) and not seen if lo>>ro (PT 7 or primitive achondrites).
Taking to~106 y (Al26) and the above ro:
|
PT 2&3 |
Do << 3*10-15 cm2/s |
|
PT 4&5 |
Do ~ 3*10-15 cm2/s |
|
PT 6 |
Do > 3*10-15 cm2/s |
|
PT 7-∞ |
Do >> 3*10-15 cm2/s |
Table 1: The values of diffusion coefficients leading to various petrologic types with primordial Al26 heating.
Now,
Do ~ Aoexp(-Qo/kT) (2)
where Qo is some energy to form lattice defects to diffuse through, in the order of 1 eV, while for the prefactor Ao, very roughly,
Ao ~ a2ν (3)
where a is the lattice length, and ν is the frequency of the (thermal) oscillations in the lattice.
We would need Ao and Qo in the temperature range cca. 500 - 1500 K, for all the major olivine, pyroxene (and feldspar) constituents. As will be seen in the next Chapter, there is no problem with olivines, but pyroxenes are more various.
Anyway, one can guess the trends via melting points Tm. Namely, until there is a simple and more or less regular lattice, Tm is determined by the same factors as ő and Qo, and then
Qo = αkTm (4)
ν = ß(k/h)Tm (5)
where k and h are the Boltzmann and Planck constants, respectively, while α and ß are dimensionless and maybe slowly varying factors. Just below Tm we get then
D(Tm-0) ~ a2ß(k/h)Tmexp(-α) (6)
and, since for all relevant materials a~3*10-8 cm and Tm~1500 K, D(Tm-0) is in the range 0.03ße-α cm2/s.
Now we can see α and ß at least for some metals and simple olivines. For many solid states ν~1014 s-1, whence ß seems 0.3 - 1. For various metals Ao=(0.01-0.1)cm2/s in accordance with (6). For self-diffusion in metals α is cca. 18, and then a formula of form (4) is told to be good for 10 % (Shewmon, 1963; Lazarus, 1960). According to these numerical factors D(Tm-0) is expected about 1.5*10-9. Then from the numbers we gave at the end of the last Chapter it is clear that if a meteorite consisted purely of metals and simple olivines, the diffusion would erase the last traces of chondrules far below melting point. On the other hand, the composition would remain chondritic.
For olivines there is a detailed investigation for San Carlos (Arizona) olivines between 10 and 40 weight % Fe (Buening & Buseck, 1973). At higher temperatures, extrapolating to pure forsterite (Tm=2163 K) Ao=0.03 cm2/s and α=14.21, while for pure fayalite (Tm=1478 K) Ao=3.4*10-4 cm2/s, and α=13.28, so α is slowly varying with composition and not too unsimilar to metals. With these values in an imaginary meteorite of pure forsterite chondrules would be erased by diffusion on 1112 K, while in pure fayalite on 848 K. These temperatures are rather low, pure olivine meteorites are absent, but the numbers show a trend.
We close this Chapter, from the great variety, with a Ca-mica, margarite, and a pyroxene, augite. Fechtig, Gentner & Zähringer (1960) investigated Ar diffusion in them, and, while that coefficient is not just valid for Al, Mg or Fe, it gives an orientation. At 1000 C° D is just below 10-10 cm2/s in margarite, but only about 10-13 in augite, showing the variety; Qo is 1.16 eV for high-temperature augite and 2.31 eV for margarite, while the corresponding Ao's seem to be 8*10-9 cm2/s (!) for augite and 7*10-2 cm2/s for margarite.
The data for the Ca-mica are not unsimilar to those for either metals or olivines; but for the pyroxene augite the diffusion coefficient is order of magnitudes smaller. This suggests that olivines equilibrate much faster than pyroxenes and it is indeed so.
TO THE PETROLOGIC TYPE 4.0 AND BEYOND
According to the previous data we may expect that equilibration happens first in olivines. Also it needs then the highest temperature in forsterite (so E3 chondrites). Taking to~106 y (Al26) and lD>>ro for olivine, D(To)>10-14 cm2/s is needed. This is 875 K. Well above this temperature diffusion is complete even in the olivine of E's, so our guess is that the state is beyont E4.0. In the same time D(To) is just 3*10-15 cm2/s for augite, so indeed some structures did not yet diffused away, so the chondrules are still seen, not quite sharp, but clear. Using augite as a model for the beginning of obscure chondrules, PT 6 one would get at least 700-800 C°, and for the beginning of no chondrules at all at least 1000 C°.
In addition observe that chondrules do not seem in E6's (Mason, 1962). If so, then they are really E7's in the present scheme, and then that stage is beyond 1000 C°.
Now let us abandon the augite model and tell simply that measurements would be needed for various pyroxenes relevant in chondrites. In the next Chapter we use scaling laws.
ON THE BORDERLAND OF ACHONDRITES
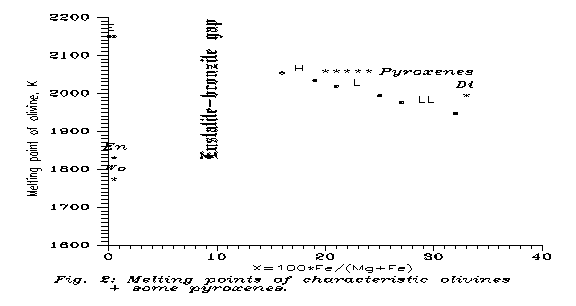
We have seen that, if the silicates do not melt before, a continuous fading of chondrules is expected, and this can be PT 7. Chondrules are no more seen, maybe everything is almost homogeneous, but the bulk composition is still quite chondritic (except maybe for Fe°, see the next Section). Now, according to the rough scaling with Tm, for which we showed examples in the previous Sections, and which is based on the fact that higher melting point means higher interatomic forces, so higher activation energy needed for lattice defects through which diffusion becomes possible, we can guess that if a specific stage has been reached at To in pure Mg-silicate (i.e. extremal enstatite), then in other silicates the same diffusion stage has been got at a temperature lower proportionally with the actual melting points. On Fig. 2 we compare here the olivine melting points, although E chondrites are rather enstatite, so pyroxenic. For C-s the situation is not so simple, e.g. serpentine may substitute the olivine.
|
|
For pyroxenes the melting points are somewhat lower, e.g. Tm is 1830 K for enstatite, 1773 K for wollastonite and 1993 K for diopside.
Now we roughly estimate the important temperatures from Fe loss.
Fe LOSS: VIA C AND FeS TOO
We do see Fe loss in chondrites. Mason (1962) definitely reports a small Fe deficiency in E5 and a serious one in E6 (but, as we saw, it is possible that these states should be called E6 and E7, respectively, from the point of view of diffusion scale). It is possible, of course, that this is not evolution, but different initial condition, and anyways, E's are rare, so the statistics is poor, but still we take the simplest explanation.
Fe° and FeS are not integral parts of the silicate lattice, and Fe specific gravity is much higher than that of the silicate. So the Fe-FeS-C mixture flows out and becomes gravitationally separate if its melting point is reached and some gravity is present. The second condition is fulfilled in parent bodies. As for the first, the exact melting point is hard to calculate, it is well below the silicate melting points. Fe° and FeS melt near to each other. The pure Fe melts at 1535 C°, but already a very small amount of C brings down the melting point below 1500 C°, while pure FeS melts at 1430 C°. The eutectic carbonated Fe melts about 1140 C°, and this needs 4.3 weight % C. Now, since in E's C is cca. 0.4 % and Fe is cca. 25 %, the bulk average of C in Fe is only cca. 1.6 %, but then some 2/5 part of the Fe can flow out at 1140 C°. In addition there is a substantial FeS content, some 1/3 of the Fe° (Jarosewich, 1990), decreasing further the eutectic temperature. In the same time the melting point of forsterite is 1890 C° (that of corresponding pyroxenes is somewhat lower), so the E silicates may exist for a wide temperature range after Fe° and FeS leaves molten, for the core of the parent body.
Fig. 3 is a three-colour graph using the data of the NIPR Catalog averaged for all combinations of chondritic groups and petrologic types. The vertical position is the total Fe/Si content, the red, green and blue constituents are the metallic, oxidised and sulphidised components. Outflow is directly seen from the vertical position. But also an iron outflow is expected to carry a way troilite too, so outflow is more certain if the colour loses a purple component.
Fig. 3: NIPR Catalog chondrites
vertical=full Fe, red=metallic, green=oxidised, blue=sulphidised
On the other hand we do not see Fe deficiency in the (average of the) H6's of the NIPR catalog, 23 meteorites, a reliable statistics (Lukács, Holba & Bérczi, 1999, LPSC 30, #1337). Now this may have 2 reasons. First, we saw that the temperature of PT 6 must be lower in H's than in E's, because of the lower Mg content. Second, both C and FeS is less abundant in H's, so melting point decrease is much smaller.
H7 meteorites are still unknown, reason is unknown. But it is sure that the temperature for PT 6 is below (albeit maybe only slightly) the melting point of Fe°.
There are 94 L6's in the NIPR Catalog. In average Fe° and FeS abundances are just the averages of all L's, and very similar to the averages of the 17 L5's. There is one identified L6-7, and it shows a cca. 15 % deficit in both Fe° and in FeS, so it is possible that Fe started to flow out, but one cannot make any statistics with a single sample.
The average of the 18 LL6's of the NIPR Catalog does not show either Fe° or FeS deficit compared to all LL's. However there are two LL7's, and their averages (albeit poor for statistics) show serious deficiency in both ferrous phases. Then the LL6 stage is not hot enough for liquid Fe (we may expect it cooler even than H6), but LL7 is hot enough.
Finally C's are found only until PT 6, they are even more fayalitic, so they are expected to reach PT 6 at lowest temperature, and we do not see indeed Fe deficit in them.
E, H, L, LL PRIMITIVE ACHONDRITES
In the present study we would like to make clear distinction between the usual achondrites, say basaltic meteorites, and the primitive achondrites. Beyond PT 6 chondrules are already absent, but the composition (with the possible exception of the Fe°-FeS-C triad) our description we used the primitive achondritic expression for H, because we should like to distinguish them from basaltic achondrites. Originally primitive achondrites was used for an achondrite with chondritic composition, but belonging to the E-H gap in the Urey-Craig field. The multiplication of meteorite samples in the last 30 years mainly by Antarctic samples made it possible to see more transitional meteorites between chondritic and achondritic stages. Introduction of E, H, L and LL primitive achondritic concepts want to make clear distinction for a stage between chondritic and achondritic (earlier mainly basaltic achondritic) meteorites. In the sequence from chondritic to basaltic achondritic stage the E, H, L, and LL primitive achondritic stages will stand between the metamorphic grade 6 (sometimes 7) and the basaltic achondritic stages of these chondritic groups.
The character of the main processes in the E, H, L, and LL primitive achondritic stages is somewhat different from those which were used in descriptions of gradual metamorphism in chondrites. The 2 processes, both distinguishing par excellence chondrites from achondrites, Fe loss by melt and metamorphism, go according to different rules. Iron or sulphide melting needs a temperature not more then 1700 K and often much lower for Fe-FeS-C mixtures, and relatively short time. On the other hand metamorphism could be described mostly by diffusion. The two processes merge only at silicate melting, as we saw at very high temperature compared to Fe melting. On the other end of the original meaning of achondrites classical basaltic achondrites were separated from their original parents, so they were able to be studied by igneous petrologic descriptions. The E, H, L, LL primitive achondrite stage study that range which is in between these two ends: between metamorphic diffusion and melt crystallizing solidification and crystall fractionation. In this intermediate E, H, L, LL primitive achondritic stage the process of separation has important role and thermal evolution is "mixed" with gravitational and rheological effects.
In one of our earlier works we could show the most crude effects of gravitation if we compared basaltic sequence of the earth and an asteroid (Lukács, Bérczi, 1998). There we found that FeO content of the basaltic sequence is far lower for the terrestrial basalts than basaltic achondrites, and this trend is valid from komatiites to recent tholeiitic basalts, in the same way than from diogenites through howardites to eucrites. Moreover, the counterparts of the high Mg bearing depleted lherzolites could be found in the high Mg bearing ureilites. We can not assert that all these differentiations (we called it "barometric height formula for silicates", LPSC XXIX, #1223) occurred parallel in an asteroid, but we wanted to show that such an effect can be observed in the statistics of the recent dataset (mainly we used the NIPR Catalog, Yanai, Kojima, 1995).
PORTALES VALLEY AND ITS RELATIVES:
SOME TEXTURAL CHARACTERISTICS OF THE METAL COLLECTING (+VEINED) H6 CHONDRITES AND RELATED II E IRONS WITH SILICATE INCLUSIONS
There are six meteorites in this clan. Three of them were classified to H chondrites, and also three were as primitive II E irons with silicate inclusions (McCoy, 1995).
Rose City: Fell in 1921, in Michigan State, USA. Its remarkable characteristics was the 36.4 wt.% total iron content. Although brecciated, it was classified as H5 chondrite (its Fa (19) is typical to the H range), which contains larger Fe-Ni inclusions as nodules. (Widom et al, 1986, Rubin, 1995. Ikeda et al, 1997.) It was shocked and contains portions which are free of metallic Fe-Ni and troilite, like as Chico, too (Pinault et al, 1999).
Y-791093: Found in 1979 on Antarctica by Japanese Expedition it was classified to H6 (Yanai, Kojima, 1995) although it contains equal amounts of metal+sulfide and chondritic portions (in vol.%). If separated, the metal+sulfied portion is texturally similar to IIE irons, the chondritic portion is H6 chondritic. However, the whole assemblage is similar to Netschaevo and Techado chondrite-like inclusion containing primitive IIE irons (Ikeda et al, 1997).
Portales Valley: Fell in 1998, in New Mexico State, USA. In some protions the metal rich veins penetrate the whole hand-specimen sample with wider and a network of thinner veins. Its metallic Fe-Ni content in some fragments is ca. 35 wt. % (vs. ca. 18 wt. % of average H chondrites, Rubin et al, 1999). Considered to have been brecciated (Kring et al, 1999, Rubin et al, 1999), or equilibrium with chondritic portion, @@ chondrite (Pinault et al, 1999). (Kernouve may also be involved to our H6+IIE-clan.)
Netschaevo: Found in 1846, in Russia. The primitive IIE iron matrix contains angular silicate inclusions, which comprise the 25 vol. % of the meteorite. Silicate portion contains relict chondrules and its refractory element content is in the range of the ordinary chondrites, although the Fa (14) of olivine is outside of the H chondritic range (Bild, Wasson, 1977). Silicate portion has not undergone melting only heating and recrystallization. It has higher Fe/Si ratio, than upper Wiik line chondrites, and this ratio is only the same for Rose City (Bild, Wasson, 1977). Its metallic portion has siderophile element content also higher (ca. 2 times) than H chondritic metal range (Bild, Wasson, 1977). With its characteristics nearer to the E-H point of inflexion Netschaevo can be considered an E-H chondrite related member of our H6+IIE clan.
Techado: Found in 1977, in New Mexico State, USA. This IIE iron meteorite contains a smaller silicate inclusion inside the iron. The mass of silicate is unmelted but exhibits a strongly recrystallized texture. Olivine (Fa 16.4) and pyroxene (Fs 15.3) relates it to H chondrite range. No shock effects have been observed on silicate inclusion, so metallic components may have been locally segregated (Casanova et al, 1995).
Watson: Found in 1972, in South Australia. This IIE iron meteorite contains the larger silicate body ever found inside an iron meteorite. The large mass of silicate, engulfed in the iron, melted during its including into iron melt, but after recrystallization it preserved its bulk composition similar to H-chondritic one, except metal+sulfide fraction (unlike to Kodaikanal silicate inclusions, which sufferred fractionation after melting, Olsen et al, 1994). The metal matrix is characteristic to H chondritic metals. It was observed, that metal sufferred shock (Olsen et al, 1994).
The collected 6 cases of the H+IIE clan meteorites has the following fundamental properties, summarized:
|
Name |
Silicate |
PT (Ch.) |
Iron |
Shock(Silicate) |
|
Rose City |
H |
5 |
IIE |
Y(brecciated) |
|
Y-791093 |
H |
6 |
IIE |
Y |
|
Portales Valley |
H |
6 |
IIE |
olivine mainly in shock st. S1 |
|
Netschaevo |
bw. H & E |
(Y) |
IIE |
N |
|
Techado |
H |
beyond 6 |
IIE |
N |
|
Watson |
H in IIE |
beyond 6 |
IIE |
? |
Table 2: Portales Valley, and some of its possible relatives. Data according to Olsen & Jarosewich (1971); Ikeda et al, (1997); Olsen et al, (1994); Kring, Hill & Gleason (1999); Rubin & Ulff-Mřller (1999); Ruzicka, Snyder, Prinz & Taylor (1999) and Pinault, Scott, Bogard & Keil (1999); Meteorite News 1996. Observe that this Table explicitly show Netchaëvo as a "chondrite in the gap": something still with a chondrule, and gap composition.
Portales Valley is the only chondrite which has Widmanstatten pattern in its iron portion. Observe that irons of all the 6 clan meteorites are of the same type, conform to iron flowing out of the chondrite matrix. As for cooling times or rates and original and/or transient heating, Pinault & al. (1999) suggest a rapid heating, metal crystallization in "months or years", Ni cooling rate in taenite cca. 5 K/My, they prefer Al26 (or similar) heating. Rubin & Moller (1999) conjecture local shock temperature up to 1635 C°a cooling rate for metal 10 K/My between 700 and 500 C° and doubts about the availability of an Al26 heating. Finally Kring & al. (1999) call the exact cooling rate uncertain, as sometimes it is claimed that rapid cooling is also conform with Widmanstätten pattern (Rasmussen & al., 1995) but for the post-impact metal cooling they guess ~10 K/My, and prefer the impact when the parent body was still warm.
A SELF-CONSISTENT SCHEME
Observe that Table B is self-consistent. All iron portions seem to be the same type, and comparing shock and chondrite type, the pattern is not self-contradictory even if, according to Occam's razor, we do not want to postulate outside source for iron.
Namely, we do know that "ordinary" H6's were not hot enough for Fe° outflow; but shock is observed in Portales Valley, Rose City and Y-791093 (and it is worthwhile to note that Y-790126, L6, with a substantial Fe° phase is shocked too; Meteorite News 1998) . For Netschaëvo and Techado, where shock is absent, the chondrite is not H6. Techado is "beyond H6", i.e. it may have had such a temperature where iron flow started (still far below the melting point of bronzite olivines) and Netschaevo is "between E and H" and we saw at least that there is outflow in E6's. In Watson where we do not show if shock happened or not, the general composition is H, but the chondrite may be again "beyond H6".
As for "between E and H", we note that regular chondrites are not found in the enstatite-bronzite gap, but such silicates occur in e.g. lodranites. It seems that in the state space there is a repulsive point (Bérczi, Lukács, 1998, Bérczi, Holba, Lukács, 1999).
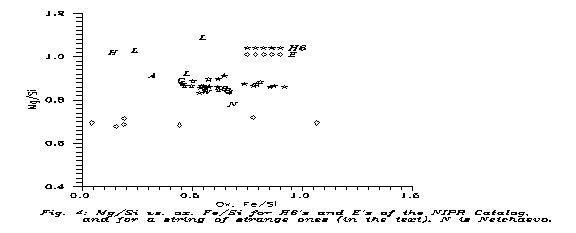
Fig. 4 shows some "suspected" meteorites, compared to both H6's and E's of the NIPR Catalog. The "anomalous" meteorites are put on the Figure in 2 groups. The first one consists of 7 Yamato meteorites which were found somewhat anomalous for the discoverers and appear in the NIPR Catalog. One (Y-74063) is a G chondrite, denoted such on the Figure, 3 (Y-74357, -75274 and -791493) are lodranites (L), 2 (Y-75097 and -793241) are L6 and here denoted by "6" and one, Y-794046, is H4, denoted by "4". We see that, at least on an FeO-Mg graph, they merge with the H6's, even if at the edge of the strip. The other group is 4 "anomalous" meteorites: ALH-85085 (H), Winona (W), Netchaëvo (N) and Acapulco (A) (Jarosewich, 1990). Interestingly enough, on the oxide Fe - Mg plane they form a straight line, but their positions, with the exception of Netrchaëvo, project onto the usual chondritic positions. Netchaëvo is clearly "in the gap".
|
|
As for the multiplicity of data about the thermal history there seems no self-contradiction either. It would be dangerous at the present state of art to decide the "Al26, Yes or No" question. We refer only dozens of asteroids down to radii 30-50 km either spherical or differentiated. Something must have melted them maybe just after condensation. If not Al26 (or Pu244) then something unkown well mimicking it. We call it for a while "Al26" in the sense of Mark Twain who stated that plays of Shakespeare were written by another person of the same name.
Now in Portales Valley we saw the shock. Then take first the normal history of the (H) parent body, the interior at H6 temperature, then a shock sometimes 0<t<to, so in the heydays of "Al26" heating. The shock increased the temperature above Fe (Fe-FeS-C) melting point and the metal solidified back for "periods greater than several weeks" (Pinault, Scott, Bogard & Keil, 1999). It seems that the cooling slowed down to 10 K/My only later, at lower temperatures. Now, this slower rate may be the normal (non-shock) cooling rate of a deep interior (Kring, Hill & Gleason, 1999), but also it is automatic equilibrium cooling if to ~100 My, which is so if the heating agent was Pu244.
In this story the shock increased normal H6 temperature beyond H6 and Fe° melting, but this increase was transient. If it lasted much less time than to (even if "over months or years"; Pinault, Scott, Bogard & Keil, 1999), then there occurred practically no change of the silicate via diffusion (so in PT) while permanent change happened in Fe° and FeS loss, which went not by diffusion but by flow.
DISCUSSION: CHONDRITES-PRIMITIVE ACHONDRITES-BASALTIC ACHONDRITES
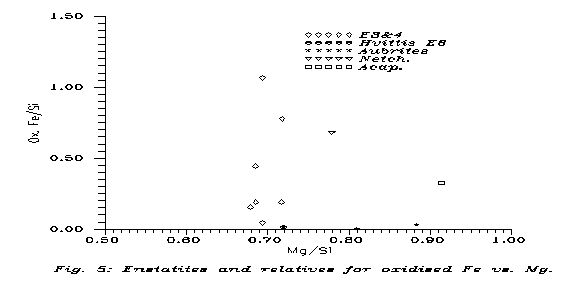
On the example of E's and relatives in the NIPR Catalog we can display the difference between primitive achondrites (of chondritic composition) and par excellence achondrites (e.g. basalts). Of course, the theory tells that primitive achondrites are connected to par excellence achondrites via iron loss,so from the ferrous components we can use only oxidised Fe for composition. Fig. 5 displays Feox/Si vs. Mg/Si for the E's of the NIPR Catalog as chondrites, E6 Hvittis to represent primitive achondrites (on the basis of Mason's (1962) remark that E6's have no chondrulae), the aubrites of the NIPR Catalog as E achondrites, Acapulco as something of E-H origin, and Netchaëvo for comparison.
|
|
Indeed, the "E primitive achondrite" Hvittis is well among the E3&4's in the metal-free plot. Netchaëvo is not, but it is not expected, "being in the gap". Acapulco is not either; the higher Mg content, compared to the almost purely Mg-silicate E's must mean that in Acapulco there is more olivine, so it cannot have direct genetic connection to them. But aubrites are also Mg-richer than E's.
So aubrites are not basalt of the E parent body (say, proto-Hungaria). If they have any close connection to such a parent body, they are rather analogous to ureilites (or in Earth, lherzolite), and then the E basalt is still unknown. For the problem of differentiation between primitive and basaltic achondrites we will return in a subsequent paper.
Portales Valley and the also rather fresh discovery of Yamato 791093 iron rich chondrites enlarged the circle of those meteorites which help to see in this complexity the borderline between chondrites and achondrites in the case of the H group. This process was going deep in the chondritic parent body, that is why so rare the representative transient samples are. In 1995 McCoy summarized the state of art at that time. His sequence was: Netschaëvo (unmelted, relict chondritic), Techado (unmelted, chondritic recrystallized, but Fe-Ni-S melted), Watson (totally melted, but no silicate differentiation), Miles and Weekeroo Station (opx-cpx-pl partial melted) and Kodaikanal, Colomera, Elga (differentiated silicates). We did not study the differentiated silicate bearing IIE irons, and with the two new discoveries of this clan the new sequence can be given such:
Rose City (only shock melted and brecciated H5),
Yamato-791093 (H6 chondritic, maybe shock induced, but "self-melted" Fe-Ni-S),
Portales Valley (H6 chondritic, maybe shock induced, but "self-melted" Fe-Ni-S),
Netschaëvo (E-H chondritic, "self-melted" Fe-Ni-S),
Techado (unmelted H primitive chondritic, "self-melted" Fe-Ni-S),
Watson (melted but recrystallized H primitive chondritic, melted Fe-Ni-S).
********
Now the question is: If there was only one H parent body, as sometimes assumed, why do we not find H7's, while in general metal-veined chondrites are not rare; Ruzicka, Snyder, Prinz & Taylor, (1999).
ACKNOWLEDGEMENTS
The authors would like to thank Drs. K. Yanai and H. Kojima for illuminating discussions. Partly supported by OTKA T/026660.
REFERENCES
Bérczi Sz., Holba Ágnes & Lukács B., 1995: Acta Min. & Petr. XXXI, 53
Bérczi Sz, Holba Ágnes & Lukács B., 1996: KFKI-1996-15
Bérczi Sz., Holba Ágnes & Lukács B., 1999: LPSC XXX, #1014
Bérczi Sz., & Lukács B., 1998: 23rd Symp. Ant. Met. Tokyo, 4
Bérczi Sz., & Lukács B., 1999: LPSC XXX, #1275
Bild R.W., Wasson J.T. 1977: Science 197, 58
Buening D. K. & Buseck P. R., 1973: J. Geophys. Res. 78, 6852
Casanova I., Graf T., Marti K. 1995: Science 268, 540
Fechtig H., Gentner W & Zähringer J., 1960: Geochim. Cosmochim. Acta 19, 70
Hutchinson, Alexander & Barber, 1987: Geochim. Cosmochim. Acta 51, 1875
Ikeda Y., et al. 1997: Antarctic Meteorite Research 10, 335
Jarosewich E., 1990: Meteoritics 25, 323
Kring D. A., Hill D. H. & Gleason J. G., 1999: LPSC XXX, #1618
Lazarus D., 1960: Solid State Physics 10, 71
Lukács B., & Bérczi Sz. 1996: 21st Symp. Ant. Met. Tokyo, 90
Lukács B., & Bérczi Sz. 1997: LPSC XXVIII, 853
Lukács B., & Bérczi Sz. 1997: LPSC XXIX, #1223
Lukács B., Holba Ágnes & Bérczi Sz. 1999: LPSC XXX, #1337
Mason B., 1962: Meteorites. J. Wiley & Sons, New York
McCoy T.J., 1995: Meteoritics 30, 542
McSween H. Y., 1987: Geochim. Cosmochim. Acta 51, 2469
Meteorite News 1996: Vol. 6, No. 1
Meteorite News 1998: Vol. 7, No. 1
Olsen E. & Jarosewich E., 1971: Science 174, 583
Olsen E. & al. 1994: Meteoritics, 29, 200
Part I: see Bérczi, Holba & Lukács (1996)
Pinault L. J., Scott E. R. D., Bogard D. D., & Keil K., 1999: LPSC XXX, #2048
Rasmussen K. L. & al., 1995: Geochim. Cosmochim. Acta 59, 3049
Rubin A. E. & Ulff-Mřller F., 1999: LPSC XXX, #1125
Ruzicka A., Snyder G. A., Prinz M. & Taylor L. A., 1999: LPSC XXX, #1645
van Schmus W. R. & Wood J. A., 1967: Geoch. Cosmoch. Acta 31, 747
Shewmon P. G., 1963: Diffusion in Solids. McGraw-Hill, N.Y.
Wasson J.T., Wang J. 1968: Geochim. Cosmochim. Acta 50, 725
Yanai K. & Kojima H., 1987: Photographic Catalog of the Antarctic Meteorites. NIPR, Tokyo
Yanai K. & Kojima H., 1995: Catalog of the Antarctic Meteorites. NIPR, Tokyo
Zolensky M. E. & al., 1997: Geochim. Cosmochim. Acta 61, 5099
My HomePage, with some other studies, if you are curious.