ON THE CONTINUOUS DEVALUATION OF THE ROMAN CURRENCY

B. Lukács

CRIP RMKI

H-1525 Bp. 114. Pf. 49., Budapest, Hungary

lukacs@rmki.kfki.hu

ABSTRACT

Roman inflation in Imperial times is a test on various theories about inflation. Roman currency was based on silver, immune to inflation, while social & budget problems, leading in modern times to inflation, were present since Late Republic. Now, inflationary tendencies were totally absent in Late Republic, were very slight in Early Principate, while were as strong as in modern developed countries in III^nd century AD. Maybe this example helps to understand better causes & mechanisms of Inflation.

1. INTRODUCTION

Economics as a science is rather equivocal about the importance of the value of the currency unit. However economics is unequivocal about the expert status of Hungarians about inflation. Hungary has a world record about inflation. Here, for international community, I refer [1]; for details I tell as follows. At the end of World War II, shortages of various kinds drove prices upwards. The situation was used first by Communists in the government, who did not like money at all, and also wanted to solve short-term financial problems. Then after a time Social Democrats believed the inflation useful, according to the advices of Hungarian economists but English experts Lords Káldor & Balogh, who believed that the old currency should be fully eliminated before introducing the new one. Therefore in 1.5 years (between the beginning of 1945 and late summer of 1946 the currency went down to 7.5*10^-21 of its real value (as far as this could be determined). Anyways, originally a banknote of 1 pengô (the currency unit) was something substantial, worth roughly a kilogram of lard, some liters of cheap wine, or some ten of tram tickets in Budapest. Now, in June 1946 banknotes of denomination 100 million billpengôs were in regular use; a billpengô was the short name for a billion pengôs, and note that Hungary is in Central Europe, so a billion is here 10¹², not 10⁹ as in USA. So the banknote was valued to 10²⁰ pengôs. The banknote for 10²¹ pengôs was then ready, but instead for more 6 weeks the State introduced a virtual currency called Adópengô or Taxation pengô, whose parity to million billion pengôs were determined by the Hungarian National Bank daily, in early mornings. During this inflation Hungary remained substantially a market economy.

Then, this story is generally the illustration of the essentially nominal nature of modern paper currencies. State can do almost anything with them and there is a general tendency to inflate them (although there are some news about Japanese Yen just deflating). This would be impossible with a currency of noble metal (says Economy).

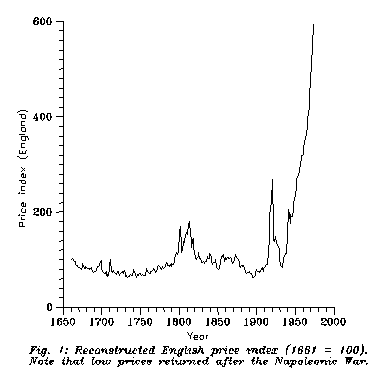
Indeed, look at the English pound. Originally it was a golden coin. At the end of XVIII^th century pound existed only in banknotes, but the guinea, a coin of 21 shillings, remained of gold. (One pound was 20 shilliings.) With the exception of years around World War I the pound was convertible to gold until the Big Depression in 1929-33; and see Fig. 1 showing that there is no important difference between the "real value" of pound in 1661 & 1931. I would not go into the details of the calculation of such a "real value"; the principle is the same as the "tourist parity" of two currencies: you form a "basket of goods" acceptable in both societies, and calculate both prices of the basket. Readers can consult with Ref. [2] about the details for English pound.

Also you can see the exponential inflation of pound after World War II. And note that Hungarian experts of the famous Hungarian inflation Lords Káldor & Balogh were the experts of British Labour, taking the Government in 1945.

Obviously such an inflation would be impossible with a gold/silver currency. With a silver money, money has its own substantial & natural value.

And now I am going to show an example for long-range substantial inflation of a currency of noble metal: the Roman denarius. The case is extremely well-documented, with hoards of surviving coinr and with ancient written documents.

2. ON THE ECONOMIC THERMODYNAMICS OF BRODY, MARTINAS AND SAJO, CORRECTED (OF COURSE) BY LUKACS

Money has a special role in Economy. Marxist Political Economy (anything that might have been) was fanatic about this, defining the special role as "general equivalent" meaning that the currency is accepted for anything else, so making market possible. Karl Marx formulated 5 points making currency (and especially golden/silver currency) feasible and useful. I do not want here to discuss too much this question; with all his shortcomings Marx was better & more conservative economist than Keynes, and his 5 points are not absurd. I take only 1 point: that the technology to get noble metals changes slowly, so "roughly the same number of workhours" is needed to produce a pound of pure gold for centuries. This is indeed so, because of a number of physical facts.

Let us restrict our attention to 3 metals, Cu, Ag & Au. All are in the first column of the Periodic Table, so in some aspect analogons of each other. Namely, all three have a single electron on the outmost shell, therefore they are all good electric conductors; but this fact is unimportant for finance. They are mutually quite well mix to form alloys. These alloys are also much used. Gold+silver is electron (! really), and was used for Earth's first real coins in Lydia, VII^th century BC. Silver+copper was always used for silver coins, because a small amount of copper lends much stamina to silver. (It is too easy to deform pure metals; two lattices differing only in a shift are almost the same.) Gold+copper is tumbaga; I do not know about tumbaga coins, but Mesoamerican jewellery used tumbaga much. Now, the Cu>Ag>Au sequence shows a few unidirectional changes.

Atomic Number and Specific Gravity. For both the sequence is Cu<Ag<Au. All of them are fairly heavy. Because of the sequence, Au is the rarest, because at 1 sec < t < 10⁶ sec, 13 billion (USA) years ago, in primodial nucleosynthesis, everything started from H, and later, in cores of stars, the processes started from H & He [3]

Electric & Thermal Conductivity. Because of the only electron on the outernmost shell all of them conduct quite well. Explanation is a routine in solid state physics, see e.g. Ref. [4]. Ag is the world recorder.

Colour. Cu is red, Au is yellow. Ag is quite white. This is not really a difference of principle. All three have smooth reflection spectra (expected from the metallic structure, common π-electrons, Valence 1 & such). Simply the spectrum is smoothly growing with wavelength for Cu, has a maximum somewhere for Au, and is rather constant for Ag.

Standard Potential. The sequence is Cu<Ag<Au. They react in opposite sequence with free oxygen. Water does not corrode them, because hydrogen is more bound to oxigen than to them.

The above qualitative properties are given quantitatively in Table 1.

Metal	Atomic weight	Spec. Grav. g/cm3	Conduct. electr.^*	Cond. th.^*	St. pot, V
Cu	63.54	8.9	94.4	88.6	+0.34
Ag	107.88	10.5	100	100	+0.80
Au	197.0	19.3	67.2	69.6	+1.38

Table 1. Characteristic data for 3 Column 1 metals. ^*: Normalised to Ag=100.

Now you can see. Copper, silver and gold are 3 variations to the same theme; gold is rarest, densest, most colourful and chemically most stable. In addition it is softest, so practically unfit for tools. Therefore it is best for jewellery; and for general equivalent.

But this suggests that very probably gold was the First Metal [5]. Without any chemistry at all, colourful & inert gold was found in nuggets first. You may argue if the second was moderately abundant and quite colourful copper, relatively rare however in metallic state, or much less abundant and white, but much more frequently metallic silver. We do know that the Au/Ag parity was in Old Ancient Ages 8, in Classical Ancient Ages 12, and now ~100. Indeed, some guesses exist that during the Old Empire of Egypt silver might have been more expensive than gold, and that might have been the reason for the name of the Egyptian Treasury: The Silver House. This may or may not be correct.

However, the technology to produce gold did not change too much from Late Neolithe to Middle Ages. You were looking for native golden veins, or you washed riverine sand using sheepskin, as the Argonauts. The tremendous technological development between 6000 BC and 1500 AD led only a slow decrease of work hours/troy ounce of gold, while Copper & Bronze Ages developed the production of copper from ores, and Middle Ages the same for silver. And, while native copper is not unheard of, bound copper is more by orders of magnitude in Earth's crust than the metallic one.

But even gold is an industrial product. In principle, gold was similar to bronze, produced from raw material (e.g. from the rock). In the same time, in modern economic theories Money is something special, while in Ancient Ages Economics was not a quantitative enough theory [6]. Fortunately, Thermodynamic Economics of Bródy, Martinás & Sajó [7] has the appropriate form to handle just this problem. To be sure, Ref. [7] had some inconsistencies which Martinás forbad to discuss for me, so I had to correct them in another paper [8], and so you should read refs. [7] & [8] together (not a problem; if you can get [7], you can get [8] as well), but still the formalism is good to understand Inflation.

There is a National Economy. What are the macroscopic quantities to describe the actual Wealth of the Nation?

Obviously you can select a set of commodities Nⁱ. You can either take the yearly productions or the actual quantities; the second is better but the first is easier to be done. Also, you must take the total population P using the commodities, or a part of it, the labour force L. (Ref. [7] neglects P. In contemporary First and Second World Economies P is almost constant, and you may ignore a constant extensive.) And, of course, there is Money M.

So you have the set

{(P), M, Nⁱ} (1)

Now, there is a Wealth. It is more or less the Sum of Average of the individual well-beings, so a homogeneous linear or of homogeneously first order function of all variables, S, so

S = S(P, M, Nⁱ) (2)

S = X^R∂S/∂X^R (3)

X^I = {P,M, Nⁱ}, ^I=^ø,⁰,ⁱ (4)

where, and henceforth, the Einstein convention is used: there is a summation for occurring twice, above and below.

We do not know a priori the form of the function S(P,M,Nⁱ). Surely it changes from society to society. However, eqs. (1-4) are homologous to Thermodynamics. The missing 2^nd Law can be got by an evolutionary reasoning:

The Society will prefer processes advantageous for the Society. So, except for negligible fluctuations, S will not decrease:

δS≥0 (5)

for some processes analogous to adiabatic ones. Surely δS=0 for pure commerce.

Now, surely, the form of the utility function (2) should be a goal of social "sciences"; instead of they have some superstitions, leading to political differences. For any case, the second derivatives must form a negative semidefinite matrix, otherwise instabilities occur and the state is impossible for any reasonable time length (a situation well known in the theory of phase transitions). The negative semidefinitivity is well known in economics too: "the second dish of soup worths less".

You can form first derivatives of S as well. From thermodynamic analogy we can write:

Y_I = ∂S/∂X^I (6)

Now, for I=0 we get an equation very important for the European Union, containing information about the reproduction of manpower or population; but that would be another study. For I≥1 we get:

-µ_i/T = ∂S/∂Nⁱ (7)

for I=0

1/T = ∂S/∂M (8)

and for I=ø:

1/T = ∂S/∂M (9)

which you may simply read as definitions for µ_i and T.

Subsystems in contact of course (behind this phrase is Second Law) will equilibrate T & µ_i. So there are "natural" market prices and a natural 1/T in the society.

For further discussions we must see the dimensions of X^I and Y_I. That is simple enough.

Eq. (1) defines X^I. I ignore here P. Nⁱ is measured in natural units. So if we are concerned with raw iron, then the unit is maybe ton of raw iron, and if it is sheepskin then it is number of sheepskins. N⁰≡M needs a discussion; but currency has a currency unit. So it is HUF; or, in exotic countries, maybe US$.

Now let us see the intensives Y_I. Eq. (3) shows that Y_I times X^I must have the same dimension as S, utility. S may be dimensionless (for simplicity I choose this), or may have a definite dimension well argumented.

Now, from eqs. (2-5),

µ_i = -∂S/∂Nⁱ/(∂S/∂M) (9)

[8]. So you can see the following:

Assume that a State redefines her currency unit by cutting zeros. This was done in the sixties be Soviet Union & France (they have cut two zeroes), in the near past by Poland (by four zeroes and there are rumours about also about Romania), and it just have happened in Turkey (6 zeroes). Of course, except psychology, nothing happens. Surely, social utility will not change with the name of currency. (Look at the absurd conclusion about "good" and "bad" currencies in [7].) So then µ_i scales as the currency unit. Consequently (for more discussions see [7] & [8]) µ_i is simply the equilibrium market price of commodity Nⁱ.

But then 1/T is the utility of a currency unit; by other word the "purchasing power". If you have one plus HUF, you are "better off"; 1/T tells, how much so.

Now, imagine that M is a paper money. Then State can do anything. She may define M in a time-dependent way, for example, and then there is problem (with the thermodynamic formalism [8]).

However, assume that M is on silver base. Then the unit of M is a canonical silver unit, say, of weight one ounce (troy or not). Still State, by her monopoly, can increase the value of the coin. Still, the market value of the coin must not be independent of the market value of such amount of silver, m_cµ_Ag.

And now let us see.

3. ROMAN MONETARY HISTORY

We know that for a long time Romans had simply weighted metal in the purchase. The Twelve Tables write about scales in purchase. Also it seems that the main commodity to be weighted was copper (aes means metal; but almost always copper metal). Then the developing Republic introduces standardised money.

The monetary history of Rome is well studied. Without pursuing completeness, see e.g. Refs. [9] & [10] as books and [11] & [12] as Internet sites.

It seems that the first standardised money was one pound of copper. Note that one "pound", libra, is only 327 gram or 12 ounces. It seems that the money of Old Republic was based on As, 1 libra of copper.

This monetary system, however, was not good for foreign trade. So in 268 BC the cosmopolitan Republic introduced a new unit. As coins had been reduced to third in weight; but 10 new asses were exchanged into a silver denarius, meaning simply 10-piece. Since denarius is a silver coin, foreign merchants will accept it. For order of magnitude it is similar of a drachm (Attic or not); but even Cosmopolitan Romans are not so cosmopolitan as to introduce Greek units. From now denarius will be the unit.

The Republican denarius had its weight just above 1 gram, and was 90+ % silver. The small percentage copper is for durability.

In 211 BC a small monetary reform happened (during the Second Punic War). The denarius' weight went down by a few percents, and the as' one substantially. From that time the as was just 1 ounce of copper; and 16 asses gave a denarius, not 10.

Then comes the Imperium, the social tasks (all Roman citizens have the right for sharing something; wheat? ludus circensis? lots of lands outside Rome are the properties of all Romans). And then the Emperors start to debase the currency.

Copper coins are minted by the Senate, silver ones by the Emperor, but there is (should be) a constant rate between them. What happens, if the Emperor increases the copper content of the silver coins?

In first approximation nothing. Only really substantial copper admixture can be seen in silver. No doubt, because of the electron shell similarities between silver & copper.

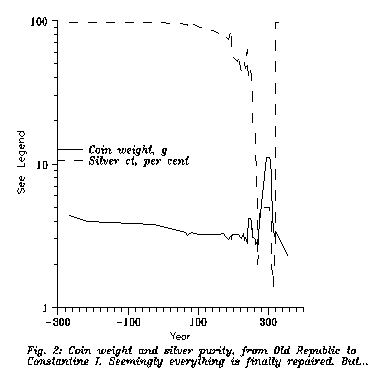
Fig. 2 is a graph for the weight and silver content of the technically dominant coin. But first I must tell what is not seen. The solid curve is the denarius until Emperors Pupienus & Balbinus, although Caracalla in 215 introduced the radiate antoninianus. (It always showed a portrait of the Emperor, with radiating rays around his head.) You can see that the weight of the denarius coin decreased very slowly, but its purity decreased faster from Traian.

It is told that Caracalla introduced the antoninianus as a dirty trick: he declared that it was 2 denarii worth, but it did not contain the metal value of 2. (Otherwise still the units of the early principate were used, [13], [14].) With this trick Caracalla introduced practically a double standard, and since in Economic Thermodynamic Money M has the role of Energy E, such economies are the analogons of the rather exotic physical systems having two internal energies. The most familiar such system is the LiF crystal: one energy builds up from the lattice oscillations, the other from the nuclear magnetic momenta in the lattice points [15]. There is very weak coupling between, so the two different temperatures can be demonstrated even for a minute. Modern economy with a double metal standard worked at the end of 1860's in the Double Monarchy of Austria and Hungary (gold + silver).

Heliogabalus in 219 demonetized the antoninianus coin, but Pupienus & Balbinus reintroduced it in 238, and henceforth the antoninianus was the fundamental coin. Denarius still continued for a while as the change for antoninianus; and anyways as a legal unit. So an antonianus was 2 denarii worth.

However this antoninianus lost in 35 years some 40 % of its weight; and, what is more, its "purity" went down to 2.5 (!) %.

A coin containing 2.5 % silver and 97.5 % copper is still a silver coin because

1) it is minted under the auspices of the Emperor, not of the Senate;

2) if you put the fresh coins into a barrel filled with seawater, the surface will be somewhat silvery. (From the surface layer seawater or very weak acids solve out some copper, as if the coin were coated with silver; but the physical process is "coating with negative copper). So the freshly issued radiate antoniniani were silver coins enough [16]; State did not take any responsibility for later handling.

But of course Emperors knew what were they doing; and greater Emperors felt some shame. Philippus Arabs, under whom the millenial demonstrations of Rome were held, increased the purity in two steps, from 41.5 % to 47 %. After 26 years Aurelianus, the great warrior Emperor doubled (!) the purity of the antoninianus, from 2.5 % to 5 %, and increased the weight too. From this time not 2 but 5 denarii equalled 1 antoninianus. He even issued a small quantity of denarius coins again, with some percents of silver. Tacitus in 276 doubled even this "purity", but his successor Probus returned to the Aurelianian standard [17]. And in 293 Diocletian again reformed. As fundamental coin he introduced the nummus, 5 denarii. In 299 the "parity" to denarius was 12.5.

As for a general overview just before Diocletian's Monetary Edict, so, say, in the spring of 301, the different official monetary units were officially exchanged as:

1 argenteus (pure silver) = 4 nummi

1 nummus = 5 radiates (antoniniani)

1 antoninianus = 2.5 denarii

but the system was based on the nummus. Then the Monetary Edict devaluated the denarius by half, so after it 1 nummus was 25 denarii [17], [18].

It remained so until 320, when Constantine I, another reorganisator of the Empire, minted again good silver coins, the argenteus, as

1 argenteus (3.36 g, good silver) = 12 nummi (a few % silver)

1 nummus = 25 denarii (practically nonexistent)

It is pointless to continue. Constantine I practically founds the Byzantian Empire.

4. ON METAL VALUES

Now let us stop for a moment. We know lots of coins; the weights and purities reported in books can be checked by measurements. So we can see if the system was self-consistent or not.

Diocletian's argenteus is told to have been 99 % silver and of 1/96 of a Roman pound, while his rather coppery nummus was 1/32 of a Roman pound. Silver/copper parity is told for ancient times 51 [11].

So a nummus coin had the thrice of the weight of the argenteus, while the argenteus was 4 nummi. Is it possible?

Let us use the weight of an argenteus as unit, and let us calculate in silver.. Then the real (metal) values of the coins are as follows.

1 real argenteus had the value in ideal argenteus as

0.99 + 0.01/51

Now the nummus has in it x silver and 1-x copper. So its value is

3*(x + (1-x)/51)

Since we know that the nummus was 1/4 worth, hence we get to the silver content x that

x = 0.0642

Instead, the sources tell that Diocletian's nummus contained 5 % silver, not 6.42 %. Then either the measurements are not exact, or really the mint stole some silver. However the difference is not big. Money still had its metal value, more or less.

Rome had gold coins too. It was almost pure gold, again some 99 % pure, and the weights of the coins are shown on Fig. 3. (Gold coins were never used in everyday life, only really rich people used it.) You can see that after 350 years the gold coin still retained more than half of the original real value.

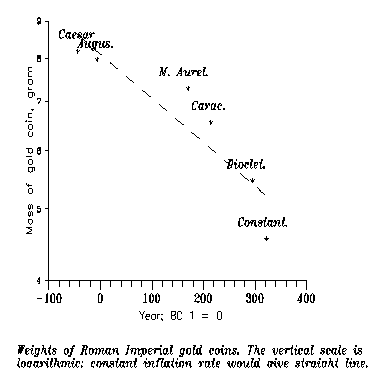
Fig. 3: Golden coins of Rome.

Now, gold/silver parity is reconstructed as 12. (This number is often repeated, now I used [11].) Diocletian issued aurei, 1/60 pound. Then the metal value of an aureus expressed in argentei seems to have been

12*(96/60) = 19.2

while it seems that it was exchanged for 24. Either there was Double Standard, or we do not know correctly the gold/silver parity! If parity had been 12, it would have meant that gold coins were overvalued. So then if one got gold coins from State, he was tempted to change it into silver; but banks were not state-owned. So what happened with the gold accumulating in banks? Did they sell back to State on official rates? What does it mean that the gold/silver parity was 12?

In a variant of Diocletian's Price List (his Monetary Edicts vary somewhat) it is stated that the price of 1 pound gold is 50,000 denarii. Let us calculate.

One pound silver is coined into 96 argentei of Diocletian, each the equivalent of 50 denarii in 301. So that is 4800 denarii for a pound of silver. With the gold/silver parity 12 then a pound of gold should have been 57,600 denarii, not 50,000.

In this case the gold seems undervalued, but for this there is an easy explanation. Maybe the silver coin (really the argenteus, not the debased nummus or the virtual denarius) was more worthy than its metal value; we are in agreement with the gold price mentioned if the silver coin was valuated 1.152 of its metal value. Of course, you cannot exchange a silver coin of 1/96 pound weight for 12/96 pound of silver; such an exchange would not be reversible, so economic utility S would change, so it would not be pure commerce. Namely after the purchase you are there with the silver. Now you try to reverse the situation via another market process, but clearly, nobody will give you an argenteus for the silver of the argenteus. Two things are missing. First the minting process, which have its own expenses. Second, the right to manufacture the coin. The State can make income from the monopoly.

So we can guess that the purchase value of the silver currency was some 15 % higher, than the metal value. That is not yet paper money.

And nobody (I mean, neither I, not Martinás, Bródy or Sajó) ever required that money-making be a reversible process in Economic Thermodynamics. Pure commerce should be, otherwise e.g. the Gibbs-Duhem Relation does not hold, so S(X^I) will not be homogeneous linear, or something equally catastrophic happens. But minting is not pure commerce. It is production; pure commerce happens by means already existing coins.

5. SO WAS INFLATION IN ROME OR WAS NOT?

Now the question is: did the Roman economy exhibit inflationary tendencies or not? On one hand there were tendencies in the society which in modern states result in serious inflation. On the other, the currency was not fictive; it was based essentially on the metal value of the coins; and how could inflation go by if the currency is based on something of real value?

Of course, there is a correct theoretical answer, which is, however, not operative. In [8] I treated the question of inflation. Inflation means a time-dependent measuring unit of Money. Note that in Economic Thermodynamics all other variables have natural units [7]. Now, in any thermodynamics-like formalism the fundamental form of the thermodynamic potential S(X^I) has to be explicitly time-independent; otherwise the Gibbs-Duhem Relation would not hold. With paper currency, of course, State can govern the scale at will, so it can quite be time-dependent.

Now, assume that for an economy you have time series of all important market prices. Then there is a scheme to calculate S(X^I); if the equations are not integrable, then some Axiom does not hold (no Thermodynamics) or we just use a time-dependent unit for Money. Then we can look for a time-dependent rescaling. When the Gibbs-Duhem Relation becomes OK, you just have the inflation-free “true” scale of money, so you got the scale of inflation too [8].

We have one very detailed price list from 301 AD, in Diocletian's Edict, and a great mass of accidental and sometimes inconsistent data dispersed along centuries, mainly but not exclusively, for food. I do not know if it were enough to reconstruct the form of the utility function S(X^I); but definitely I cannot do it now. But not so theoretical but still approximate methods are possible.

For example you can construct Consumers' Baskets. Take an average family, and sum up their consumption, say, for a year. Some bread, some meat, some wine, some oil, some clothing &c. Then you may calculate the prices of that consumption twice, in different times or in different countries. I mention here a still unpublished result telling that using a moderate Consumer's Basket constructed for Romans of the time of Diocletian, but evaluated also for Hungary in 1992 the result was that 1 denarius from Diocletian's time would have amounted 3.06 HUF of 1992.

Of course, the method has its problems when used along too big time. There is an example of Bródy [19]. Imagine that you can calculate a Hungarian inflation rate between second halves of XIX^th and XX^th century, or the change of wealth. You can form a Basket in 1870, and can evaluate its price in 1870 and in 1970. However if you form a Basket representative for 1970, some items you find nonexistent in 1870. Or, backwards, the 1970 Basket contains a wretched aluminium pot, but that pot had extraordinary price in 1870; then aluminium was still a metal for jewellery.

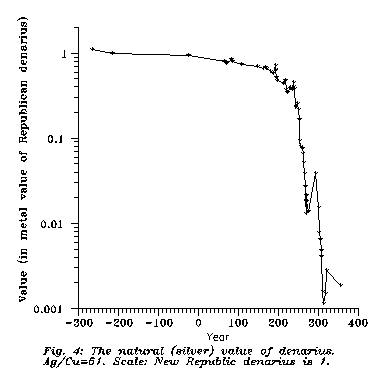
Still you can compare prices of Baskets for small steps in time, and then we can integrate up. For this, however, sociology is needed, so here I make an even simpler approach. We have seen that the value of Roman money was still near to its metal value. So I calculate the metal values of the Roman denarius from the First Punic War to Constantine I, and normalise it in such a way that the 211 BC denarius be the unit. The result is seen as Fig. 4.

You can see the accelerating loss of value in the III^rd century AD. Such a curve is rather indistinguishable from inflation, while the currency is based on its real, metal value. How was it possible?

The main tricks were told above or are seen from the curves. In principle it was difficult to diminish the weight, that being an integer ratio of pound or ounce; still it decreased, very slowly. But it was simple enough to substitute some silver with copper. Within a few years you cannot make a change from 80 % silver to 50 %, that could be detected even with 3^rd century chemistry; but you can change from 80 % to 76 % and no scandal will happen. Emperors did this; and when the summed result was too much, they introduced a new denomination.

The final result is Fig. 4; a more than 2 orders of magnitude debasement in 2 centuries between Traian & Diocletian. European historians before the last World War made the fate of the sestertius & denarius a laughingstock. And now?

English pound is continuous from Middle Ages, and the price indices between 1661 & 1931 differed a mere 3 %. And now? In early books of P. G. Wodehouse protagonists borrow ten shillings and have problems to pay back. Italian lira was continuous through World War II, but the 10 lira coin was a substantial silver piece in the 30's, while you practically could not buy anything with a 10 lira coin in the 80's. As for Hungary, Hungarian Forint, HUF, is continuous from August 1, 1946, but prices went up in 58 years more than a factor 10². Price of standard white bread since 1978 (so in 26 years) multiplied with a factor 50, sugar with 20, and of beer with 50. That is a yearly 10 %. The average yearly inflation in Rome during Imperial times was no more than 2 %. Who is laughingstock?

6. ROMAN INFLATION: WHY JUST IN THIRD CENTURY?

Historia est magistra vitae. It is hard to doubt that the process we see in III^rd century Rome in an inflation. Familiar picture: in the second half of XX^th century we saw inflation everywhere in Europe, and just now we see it anywhere, except, perhaps, Japan. And, while John Maynard Keynes believed inflation good, now the common opinion is that it is bad enough. Either necessary but bad, or unnecessarily bad.

Many different explanations exist for inflation. Some of the possible reasons did not exist in ancient Rome. Some did exist, but caution is needed, and maybe Fig. 4 can be used in choosing between them.

Surely inflation offers a short-range solution for State in fiscal problems. Then: what is common between late XX^th century Developed Word and III^rd century Roman Empire, while it acted only moderately in II^nd century, practically not in I^st century, and absolutely not in Republican times?

Obviously, I do not know the answer. If I knew, I would send this study to a respectable economic (or thermodynamic) journal. However I can disprove some popular opinions.

For example, for first sight it seems a neat explanation that inflation comes from redistribution. The idea arguments that if there is massive redistribution, then there is more demand than goods. This results in deficit of the budget, and the simplest way to make financial balance is to make more money. Generally only State can make new money; so if State has paper money, they simply print too much. Then there is more Money than goods on the market, so the equilibrium prices go up. With silver money this way is not so simple; but adding abundant copper to silver, State (Mint) can produce more "silver" coins than in previous year.

Now, I do not doubt that this was/is an important factor in late XX^th century World Economy. E.g. look at Fig. 1. Great Britain was the most traditional developed country in the second half of the century, and it was one of the 4 true winners of World War II. Now, you can see a fourfold increase of the price index in 25 years just before 1972.

What about other players of World War II? Germany's Mark practically died out; when it restarted it was slightly more stable than other European currencies. Japan's Yen and Italy's Lira survived, but lost very much in value: Italian Lira went down to below 1 % of its prewar value. As for winners, US $ remained the most stable (it remain convertible to gold until the 70’s), in Soviet Union there was no inflation, generally in no Second World country except Hungary, because State prescribed prices; but in France Franc went down to cca. 1 % of the original value until the 60's. Same problems for winners & losers?

Well, let us remain at Great Britain. We do know that Labour government started with leveller economy, nationalisation of private enterprise, plus there were costly reconstruction projects after the war. So there was budget deficit, State adopted Keynesian theory, and printed a lot of new money. And we see the exponential increase in the price index. This was driven partially by Labour ideology about necessities, rights of dispossessed for possibilities and such. And obviously at election the parties competited for voters, and majority of voters wanted to get.

Good; and then go back first to Late Republican Rome. All male adult citizens voted. OK, lawmaker votes were not proportional; e.g. knights formed roughly tenth of the voting centurias, while they were much less than 10 % of the population. But even then, poor citizens were quite populous and we learnt about the turbulent events, the deaths of the two Gracchus brothers in almost internecine war situations, the civil wars of followers of Marius & Sulla, the Catilina revolt, then Caesar's campaign against Pompeius. During this the warring factions needed to buy followers.

In addition, propertiless proletarians were part-owners of the State of Rome. When Rome took the territories of enemies, the land and foreign territory went to the Populus Romanus. OK, some land was distributed amongst Roman farmers, while big estates were hired by rich and influential Romans. Surely, they got them cheaper than equlibrium; but even then the money went yearly to the Treasury. We know that from this money hundreds of thousands got regularly wheat & olive oil; a lot of circus events were performed, and surely other donations less recorded. In such situations we would produce budget deficit and then inflation. And still, Republican denarius was stable.

Then came the Principate of conservative Augustus, tyrant Tiberius, mad Caligula who believed himself a god greater than Jupiter, contradictory Claudius, mad Nero, then a year of civil wars, &c. And after such a century, in 82 AD the denarius is at 84 % of its Republican value!

Roman II^nd century was also the time of stable denarius. "Good emperors" rule from Nerva to Marcus Aurelius, so between 96 and 180. The "good emperors" redistributed a lot, there was not too much social conflict, but in 180 the denarius had 85 % of its value in 96!

That is no inflation at all either in III^rd century or in XX^th century standards. If silver standard prevents inflation, why did it not prevent in IIIrd century? If populism leads to inflation, why did it not lead to in Late Republic? And if Omnipotent State does it, why Early Principate was almost free of it?

ACKNOWLEDGEMENTS

I acknowledge discussions & calculations with Dr. M. Banai in 1993, and also discussions with Dr. K. Martinás about Economic Thermodynamics until 1985, when she simply forbad me to discuss the topics with her and with Dr. A. Bródy.

REFERENCES

[1] McWhirter N.: Guiness Book of World Records. Sterling Publ. Co., New York, 1979

[2] The Economist, 13^th July, 1974. See aloso: B. Lukács: KFKI-1991-08 & 1998-02

[3] Fáy Nóra & Lukács B.: Sphaerula 1, 117 (1997)

[4] Kittel Ch.: Introduction to Solid State Physics. J. Wiley & Sons, New York, 1961

[5] Asimov I.: The Solar System and Back. Doubleday, New York, 1970

[6] Aristotle of Stageira: Oeconomica Bk N° 1343a1 – 1353b26. The Complete Works of Aristotle, ed. by J. Barnes, Princeton University Press, Princeton, 1995

[7] Bródy A., Martinás K. & Sajó K.: Acta Oec. 35, 337 (1985)

[8] Lukács B.: Acta Oec. 41, 181 (1989)

[9] Harl K. W.: Coinage in the Roman Economy from 300 BC to AD 700. Baltimore, 1996

[10] Zamarovsky V.: Dejiny psané Rímem. Mladá fronta, Prague, 1967

[11] ***: http://homepage/uibk.ac.at/homepage/c614/c61404/k410-aaa.html

[12] Schroer G. T.: http://ancient-coin-forum.com/ancient_coin_articles/Denarius.htm

[13] Cassius Dio: Rhomaike historia. U. Ph. Boissevain (ed.), Berlin, 1895-1931. Book LV, Chap. 12.4

[14] Buttrey T. V.: JRS 51, 40 (1961)

[15] Purcell E. M. & Pound R. V.: Phys. Rev. 81, 279 (1951)

[16] Kern J. K.: http://www.romancoin.com/order/show16.html

[17] Sutherland C. H. V.: JRS 51, 94 (1961)

[18] Erim K. & al.: JRS 61, 173 (1971)

[19] Bródy A.: Lassuló idô. Közgazdasági és Jogi Kiadó, Budapest, 1991

My HomePage, with some other studies, if you are curious.