B. Lukács

CRIP RMKI, H-1525 Bp. 114. Pf. 49., Budapest, Hungary

lukacs@rmki.kfki.hu

I discuss the dimensionality of various spaces: some physical, some not. The latter ones include the colour space, configurational space of politics (with special attention to the 2001 autumn provincial government crisis of Western Cape), configurational space for the ideas of godhead (Holy Trinity) and that of the vowel systems of languages. Some spaces have Riemannian structure, some may have but it has not yet been shown; the last two probably do not have such.

1.1: Just 3

1.2: Is It Sure? Houdini Tricks and Spiritism

1.3: Why Just 3? Candide's Best World?

2.1: Time Is Fourth But Fourth Is Different

2.2: Light Cones and Causality

2.3: What If 5 and +++--?

2.4: What If 5 and +++--?

3.1: 4 But Curved

3.2: And If >4?

4.1: The Space of Dumb-Bells Is 5-Dimensional

4.2: Quantum Mechanics of Several Particles

4.3: Enters Relativity

4.4: Dimensions of a Double Neutron Star

4.5: Bishop Berkeley and Ernst Mach, Today

6.1: Maxwell's 3 Dimensional Space

6.2: 3 Cones: The Physiological Reason

6.3: But Why Just 3?

6.4: And the Rods? Are We Not Tetrachromats?

6.5: Pectens, Birds and We

6.6: But Some Women Are Better Than Men

7.1: Mother of All Parliaments: Tories and Whigs

7.2: Right and Left or How to Punish the King

7.3: Third Way As Second Dimension

7.4: 1900: Appears the Third Way

7.5: Tripolar Century: the German Example

7.6: Hungary's Parliaments

7.7: Is the Second Dimension Still Habitable? Hungary and

South Africa in 2002

8.1: Greeks and Others: the Happy (?) Anarchy of Dawn

8.2: Early Systems: Tripolar Trimurti, n=2

8.3: The Plus/Minus of Zarathushtra, n=1

8.4: Moses and the Prophets: the Point in Infinity, n=0

8.5: The Evolution of Holy Trinity from 50 BC

9.1: The Canonical Five

9.2: Problems: Swa Indogermanicum, Gothic IU, Slavic Y &c.

9.3: But Not Everybody Is Indo-European!

9.4: The Reason Behind Deception: 2 Formants?

First version, Feb. 11, 2002

As you can see from the list of Contents, this study is intented to be big enough. I do not know how long time will be needed to achieve a stage when I would be content with every Chapter. So I rather choose a way of continuous evolution. I am going to make the material available as soon as all planned chapters are at least skeletal and some ones have meat on the bones. Afterwards the construction will grow nearing perfection in the manner of Gaudi's Sagrada Familia. I hope it will not need so much time than that.

I think the topics in itself is interesting enough, so if somebody reads even when some parts are still skeletal, he #1 gets some satisfaction. Also some parts of it are connected with my still unpublished (or "in print") works and then I will be naturally slightly secretive anyway.

"Dimension" is a terminus technicus of physics first and of mathematics second. But for other (possible) readers its meaning may not be quite obvious. So now I define the topic. However I will not go into nice mathematical details. Namely, no physicist or mathematician would argue with me in the meaning, and anthropologists do not need the mathematical niceties. So:

A space is the sum of all possible locations. These "locations" may be almost anything. E.g. in the theory of colours a possible hue is a point in a space of colours. Extreme red, which we seem to get by a very longwave and very strong stimulus is an edge of the colour space, and when it is percepted with just unit intensity (anything this unit be), then it is a point.

If we have a theory or rather a discipline, we may have a space. Now we may ask if that space has a Haussdorff property, or a Riemannian structure, or such questions. (E.g. colour space must have a Riemannian structure because everybody can measure the distance of two colours, but the space(-time) of Relativity has only pseudo-Riemannian structure.) But now we restrict ourselves to a more fundamental question. What is the number of dimensions in that space?

If we look for a Latin vocabulary we find the word dimensio, -onis (f) with some meaning "survey". Dimensio is almost the same as mensio, only with an expressed aspect "away, apart"; and "mensio" comes from the (formally passive) verb "metior" = measure. Mensor is surveyor, architect, or possibly engineer. So "dimensio" can indeed mean some measure of the extension of a space. But which one?

Now, by agreement, the number of the dimensions of a space measures into how many independent directions the space is extended. (Extends itself?) "Independent" means "independent in vectorial sense". Instead of mathematical definitions we can turn to Aristotle (-60a), i.e. De Caelo #2, at Bekker numbers (henceforth Bk) 284-5. There the Philosopher discusses directions in Heavens, and concludes that there, and everywhere, there are 6 principles or distinctions, or what, namely above vs. below, front vs. behind and right vs. left. Now, in our language, 2300 years later, that means that his World was of 3 dimensional. Namely, take an observer and fix him. He of course can distinguish between his head and sole, face and nape, and right and left #3. Then we are going somewhere; say to Moon. We ask our fixed observer to direct, and he tells: go a hundred fifty myriad stadia forward, a hundred up and nine to left. Now of course (!?) up is positive, down is negative; right is positive, left is negative (Aristotle, -60a), and so on. So the actual position of Selene in that moment is

(+100,+150,-9)*10,000 stadia

and every geographic or astronomical position can be given by means of 3 such numbers. In the same time, generally 2 are not enough. Then the survey of World needs 3 data and not 2 or 4; so Earth and Heavens are 3 dimensional. Q.E.D.

Modern architecture helps. Lying in your bed you can look to the ceiling in the corner of the room. You see 3 edges converging in the corner with mutual right angles; and cannot even imagine more. The number of mutual local right angles is the number of dimensionality (as can be proven). However, this argument, while simple, is culture-dependent. Not everybody uses rectangular habitats. Zulu, Xhosa or Sotho huts are rather semisphericals, also Navajo huts. And the same is true for recent Mongolian yurts, which were earlier used everywhere along the Eurasian grasslands, from the Danube to the Pacific Ocean. In such a living place (I cannot call it a flat, a flat is flat) one cannot have the elementary impression of 3 right angles and must use higher geometry to prove the 3-dimensionality.

Now comes some mathematics. Physicists would prefer more rigorous treatment; others may loathe the approach. I used to tell: if I wanted to deceive you, I could do it simpler; so the formulae are evidences of my sincerity. If you are not interested, jump it over. Maybe later you want to come back and check me.

Consider situations when the positions can be characterised by means a finite set of numbers (coordinates) and the distances can be measured. We will call the coordinates of a point A as x_Aⁱ, and the distances r_AB.

In everyday life 3 points not lying on a common straight line always fulfil the so called triangle inequality

(0.1) r_AB + r_BC > r_AC

and there is equality when on one straight line; r_AB + r_BC < r_AC is impossible. Hence and from a number of assumptions for continuity and so (Eisenhardt, 1950) we get to the distance of infinitesimally nearby points with infinitesimal coordinate differences x_Aⁱ and x_Bⁱ=X_Aⁱ+dxⁱ as

(0.2) dr² = g_rs(xⁱ)dx^rdx^s

where, according to the Einstein convention, there is automatic summation for any index occurring twice, above and below. Because of the triangle inequality (0.1) all eigenvalues of g_ik are positive. The matrix g_ik represents the metric tensor of the space.

However we do have well known cases when even the triangle inequality does not hold, such is, e.g., Relativity theory. Then the matrix g_ik is no more positive definite.

However g_ik must not be degenerate, i.e. must not have 0 eigenvalues. A 0 eigenvalue would mean a combination of coordinates not changing the distances at all. If so, some coordinate is superfluous.

Let us see a demonstration. On a sheet of millimeter paper the coordinate system is ready by the printed net. Starting from an arbitrary but fixed point the coordinates can be got by simply counting the lines along the long side (x) and the short one (y), and then x¹=x, x²=y. We know the Euclidean geometry of the sheet, so the Pythagoras theorem is valid and then for infinitesimal distances

(0.3) dr² = dx² + dy²

However, if one does not believe, he can experimentally verify it on the sheet.

Now, one can take a third coordinate w, for example the time when the point was made on the sheet. Then we get that the distances do not depend on this coordinate, so it is superfluous.

Now, another example is a demonstration globe. Coordinates are shown on it as latitudes q and longitudes f. Distances can be measured by means of threads and then the formula of the spherical geomery

(0.4) dr² = R²(dq² + cos²qdf²)

can be verified. (R is the radius of the globe.) Two coordinates on the globe are sufficient; the surface of the globe is two-dimensional. Of course, the points of the surface can be characterised by their (x,y,z) coordinates as well, and then the distance is given by the 3 dimensional Pythagoras formula dr² = dx² + dy² + dz². However, being the points all on a sphere they all satisfy

(0.5) x=Rcosqcosf, y=Rcosqsinf, z=Rsinq

and the distances can be expressed via only two coordinates, q and f.

We are fairly sure that our physical space on macroscopic scales is three-dimensional. Also, we are fairly sure that the 3 dimensional space is insufficient in physics and Einstein's 4 dimensional space-time is needed; so everyday distances do not represent fully the relations of positions. Some particle physicists believe that this space-time is 10 dimensional, the extra 6 dimensions all belong to space, not to time, but Space is very narrow in these directions, maybe not bigger than 10^-33 cm. Some Philippine medicine men claim that they can go into our abdomen without piercing skin &c.; if this is true then their hands move in a fourth macroscopic space dimension, but Physics cannot find it. And so on.

The method, how to measure the dimensionality of a space if we can measure distances, is fully elaborated in physics. Let us see it, with some technical simplifications. Anyways, it is not nice to write formulae with complicated index structure in a HTML file.

First we guess a dimensionality n. For example, in the physical space we have at least n=3, since we do see 3. In the politics there are at least 2 sides, e.g. Left and Right, so the parties can be ordered at least on a line. A line is n=1. And so on. Anyway, first we choose the minimal n.

Now, we measure the distances between N different points. That is N(N-1)/2 distances. for simplicity we restrict ourselves to nearby points. If the distances are infinitesimal, then in eq. (0.2) the g_ik factors are constants. Then the N(N-1)/2 distances must be expressed by the quantities on the right hand side of eq. (0.2): the g_ik's, which are n(n+1)/2 quantities, and the coordinates x_Aⁱ's, N*n quantities.

Assume first that we measured the distances without any errors. If we believe in this, then look. If we measure enough distances, then already

(0.6) N(N-1)/2 > n(n+1)/2 + Nn

E.g., if n=3, for N>8 eq. (0.2) cannot be satisfied: for N=9 the lhs. of eq. (0.6) is 36, the rhs. is 33. Then eq. (0.2) is either not true for the 36 distances, or, if they are "miraculously" true, that may be, because all the 9 very nearby points lie in a really 3 dimensional space.

OK, but the belief that we measured the distances with 0 errors is naive. However we more or less can estimate the errors. Assume, e.g., that all of the distances were measured with a common error s, with normal distribution. Then, any distance r_AB will be in the ±s neighbourhood of the measured distance with 68% probability, in the double neighbourhood with 95% and so on. Then we must measure more distances, but sooner or later eq. (0.2) will either be impossible to satisfy even with the errors; or it will be possible, but then the space is either of 3-dimensional or not but all points are near to a 3 dimensional subspace.

If somebody likes more transparency, think of n=2. One believes first that all points are on a surface. The measurements have errors s, but measuring very many points, eq. (0.2) is still satisfied within the error s. Then this means that all points are within a s thickness around a surface, maybe exactly on the surface. If newer and newer points still come from this thin sheet, then there are three possibilities. We can calculate the distance from the best ideal surface n=2. If the big amount of these "heights above" show a cca. homogeneous distribution between 0 and some maximal D, then the points very probably are within a thin sheet of thickness D. If, in contrast, the distribution is a bell-shaped error function, then probably they are on a surface, and the deviation from the ideal surface is only a measurement error. In other cases we still do not know, what is the situation in reality; but if D is small, it is not a big difference if the space is an exact surface or a thin enough sheet. Similarly for n>2.

Up to now it was impossible to prove that n>3 for the physical space. So the extra dimensions in space are either very small (this belongs to particle physics) or it is very difficult to get into them and move into the extra directions (this is employed sometimes by spiritism, unorthodox healing &c., but seems improbable, mildly put, for physicists). However when the space is not simply the manifold on which simple points are located, n can be greater than 3. Take, e.g. rigid dumb-bells. Then any physicist knows that the position of a rigid dumb-bell is 5-dimensional. 3 coordinates give the center-of-mass of the dumb-bell, and two others give the direction of the axis of the dumb-bell.

The above construction works as well as we can measure quantitatively the distances. So it is quite good for the colour space (we shall see the details) and it is rather qualitative for the space of political opinions.

It is a general belief that there is a space of locations around us: every of us, our buildings. trees of forests, planets &c. at a given moment occupy points of this space and between two time moments they may or may not move between points. Of course, the real objects are not ideal points; then they occupy clusters of nearby points.

While for physicists of 21st century this is the idea of mythic forefathers such as Aristotle and Newton, the concept can still be formulated and we can speak of it in some approximation. Then let us do.

First we need something to measure distances. In the meter range the champion of 19th century was the thin steel ribbon, with a scale on it. For longer ranges ropes were used, for even longer ones from mountains to nearby stars triangles were built up by optical instruments. The shortest side was measured in the usual ways and the two angles on the short side, a and b were measured by optics. Then the third angle is 180°-a-b via Euclides, we can calculate the lengths of the two other sides and so we know everything about the position of the remote third point. When going downward, generally magnifying glasses and microscopes were used, checking the scales in many steps.

Looking back we see the problems. Making a triangle whose short side is between Greenwich and Potsdam and whose remote pont is a Centauri, at least 2 hypotheses, not obvious, were used: that

1) light travels in straight line; and

2) the sum of the angles of a triangle is exactly 180°.

The two problems are, even, not independent. Everybody knew that on the sphere, wher sides of triangles are sections of greatest circles, not "straight lines" not existing on spheres, the sum of the three angles are bigger than 180°. the story is interesting but now let us pass.

Briefly, the construction (0.1-6) never needed more than 3 dimensions for the locations. And since we can see 3, the obvious conclusion was that the dimensionality of "physical space" or rather of the Newtonian point mechanics is exactly three.

Speculations about a Fourth Dimension started in the second half of 19th century. The principles behind were nicely condensed by Abbot (1885) in his pseudo-novel "Flatland". There a being of 2 dimensions gets 2-dimensional impressions about a 3-dimensional, being and then writes down his 2-dimensional society for inhabitants of 3, with the suggestion that even they may become confronted with something unusual and "higher".

Lot of 4-dimensional "anomalies" had been invented and suggested. Without claim of completeness, let us see 3 groups.

A circle is a completely closed boundary on the surface but can be circumvented by flying above. So a completely closed container may be open toward the Fourth Dimension. So Fourth Dimension would provide an easy explanation for miraculous escapes, murders of closed rooms &c. A lot of such mysteries were reported.

However in a lot of cases there came explanations later. Many detective stories were written about murders in closed rooms along the lines that doors, windows &c. were opened and reclosed ingeniously. True, we can see productions in circuses when a slim girl is closed into a narrow wooden box, then the box is sawed into two, then again put together and then the girl comes out unharmed. The usual viewpoint is that surely a trick is applied, which is trade secret, but probably does not use Fourth Dimension. Houdini was able to escape seemingly complete bondages or compartments but not in a physics laboratory. Similarly, some Philippine healers claim to be able to reach our internal organs without piercing our skin. Similar practices are repeatedly described by ethnographists since early 19th century. Since the results are irreproducible by physicists, strict observation was unsuccessful and circumstances are often fishy, physicists do not regard the phenomenon as signal of an extra dimension.

The second group is Mysterious Inversion. We do not know any way to make a left shoe from a right one, although shoe industry could use it. However, let us cut a form of an impression of a right foot from thin but strong paper and move it to and fro on a flat surface. Right remains right. Now we can grab the paper piece, can elevate it in the third direction, then turn it. When putting back to the surface, it will have the form of the impression of a left foot. So one dimension higher if a right shoe is transformed into a left one, or, even better, the organism of a man turns to mirror image, then maybe a travel in Fourth Dimension happened. Maybe the first novelette about this was The Plattner Case written by H. G. Wells (s.a.); while a much better elaborated one of A. C. Clarke exists too (Clarke, 1956), the second is already post-Einsteinian, so does not belong to this Chapter.

Now, nobody observed the inversion of a shoe in controlled circumstances. Maybe we see inversion of elementary particles, but particle physics belongs to a later part. Sometimes humans are observed who are mirror images of non-existent humans; i.e. their heart is on the right side, the liver on the left and so on. It is believed that they were born so; the explanation is not complete but assumes anomaly in early embryonic development. The most romantic scheme assumes first a split of the embryo into two identical twins in a slightly late stage when chirality already starts. Then the twin embryos will be mirror images. Afterwards the "normal" one dies and becomes eliminated. Since all steps of this scenario in themselves are observed in laboratories, the whole scenario, while complicated, is much more probable than 4-dimensional wombs.

And, if something "strange" appears from a hidden source, and we cannot trace it back, there is a (desperate) suggestion that it has come from Fourth Dimension (or "from another plane of existence" which even I cannot understand, because nobody ever defined these "another planes" in any operational way). For example, some spiritists believe that ghosts come from Fourth Dimension. (A very popular book (Melchizedek 1998) states, referring to personal communication, that Toth, god of Egyptians, is really an Atlantean of several tens of thousand year old, friend of the author of the book, who, however left for another plane of existence in the early 90's, and so now is out of reach.)

The problem with these "explanations" should be obvious. In a "naive" geometry space in the fourth independent direction should remain Euclidean. But then we should see it; and we do not.

There are strong arguments that we must be happy for the dimensionality to be just 3. In an earlier work (Lukács, 1995) I collected many such arguments and some bibliography. Without claim of completeness let us see some. But I must call attention to the fact that many arguments were impossible in pre-Einsteinian times for historic reasons.

Fundamental interactions as gravity and electric force have inverse-square laws. Now, using the picture of Faraday about "force lines" in 3 dimensions an r^-2 force law means that force lines start from the source ("charge"), and, if nothing happens, go to infinity. If we surround the source with concentric spherical shells, the same number of force lines cross each shell. In a semi-popular scheme for electricity it is true because the photon does not decay.

This geometric property seems indeed fundamental. Now require it in any dimension. Then in dimension n the laws of elementary forces go as

(1.3.1) F(r) = g/r^(n-1)

Now let us calculate the potential U(r) of the force, since the conservation of total energy will be something

(1.3.2) mv²/2 + U(r) = const.

two bodies are separable if

(1.3.3) lim_(r->¥)U(r)=0

otherwise they would disturb each other even infinitely far apart. Instead of the geometric condition you may require an orthodox potential equation for the Lagrangian of the potential (the Poisson equation), but in n dimensions; that is the mathematical equivalent, with the same result.

Now

(1.3.4) U(r)~1/r^(n-2) if n>2

which indeed goes to 0; but

(1.3.5) U(r)~ln r if n=2

which goes very slowly to infinity! So it seems as if there were "not enough space" for the "force lines" to "run apart" in 2 dimensions.

A lot of no's follow hence. In Flatland gravity would not permit planet formation. Anyway, planets could not orbit Sun in a stable way. Tiny atoms could not exist. And so on.

And if, miraculously these fundamental forces did not exist and instead of them some more complicated ones organised matter into living organisms, these organisms would be hopelessly dumb. Namely, imagine a rectangular net as the model of a neural network. 1 dimensional fibres are either parallel or intersecting in 2 dimensions. So a "horizontal" fibre must intersect there all the "vertical" ones. Imagine such a brain!

I think nobody is too surprised that a 2-dimensional world is "too poor" to be nice. Then let us go to 4 dimensions.

For n=4 forces go to 0 quite rapidly at great distances; energy conservation results in the nice

(1.3.6) E = mv²/2 - GMm/r²

Seemingly everything is good.

However when solving the equations of motion for n>3 there are problems. There is always, of course, a circular orbit, but unstable. The other orbits cannot be closed; moreover they cannot oscillate between a periastron and an apastron in any ways. Only cometary "orbits" are possible, from infinity to infinity. So: no analogon of Earth in higher dimensions.

We can, of course, formulate full Quantum Mechanics in 4 dimensions, without any problem, but I will not do it here and instead argue along the uncertainty principle. It is a strong tool, it was able to reproduce even results about superconduction (Martinás & Lukács, 1984). We have a positive charge, for simplicity fixed at the origin, and a light, pointlike negative charge. We have seen the potential energy between.

However there is a kinetic energy term as well. Because of the uncertainty principle, if the wave function is confined into a volume, the average of the momentum can be 0, but the momentum is not sharp, and the square of it cannot have the 0 average. But a <p²> means a <v²>, so a kinetic energy. The result is

(1.3.7) <E> = -e²/r^(n-2) + h²/8mr²

And look: for n=3 this energy function has its minimum at

r = h²/4me²

which, with the 3 constants measured in other areas of physics, gives the correct hydrogen size of chemistry. By other words, the groundstate of H atom is unique and is without any motion in expectation value. The electron is stably sitting on the proton, forming the proper atom.

However for n=4 there is no minimum in the function (1.3.7). If h>2em^1/2, then the "atom" cannot be bound. Otherwise it is bound, but the total energy has its minimum at r=0, so the atom collapses. We have then a neutral something at particle sizes, another neutron. One does not expect too much structure having evolved in a 4 dimensional world.

And so on. It seems as if Physics would tell that 3 dimensions of space results in the best possible world. Are we simply fortunate?

We shall see that such an answer is too naive; but there is some truth in it.

The years of Einstein in Switzerland were indeed happy and still somewhat naive. Of course I mean physics, not private life. Still, it is tempting to tell that

all pairs in love seem naive and ridiculous for a third person (in physics, briefly: Observer);

a physicist is doubly ridiculous when rutting or chirping as some birds in love, just for being physicist whose usual style must be very rational;

a chirping physicist is trebly ridiculous for another physicist;

and then two physicists chirping for each other are ridiculous enough. Then read the Einstein-Marity Love Letters (Renn & Schulmann 1992) #4.

And now back to physics proper. In 1905 Einstein explained the very disturbing negative result of the Michelson interferometry by mixing space and time coordinates (Einstein, 1905), and 3 years later his former teacher Minkowski showed that Einstein's operations are rotations in a 4-dimensional pseudo-Euclidean space, the Minkowski space, whose coordinates are the 3 space coordinates and the time value, together.

This Chapter is superfluous for physicists. But I hope not all the readers will be physicists,

The negative result of the Michelson interferometry was one of the greatest surprises of 19th century experiments. The interferometry was only a tool. The aim was to measure the velocity of light in a coordinate system fixed to Earth in different directions, in order to detect Earth's travel in Absolute Space (the 3-space of Newton; the 3-space discussed in previous Chapter). It was impossible to measure velocities directly with the necessary accuracy, so light was reflected at the end of path, and the differences of running times were measured in 2 orthogonal directions. Nothing was seen.

Now, the result contradicted Common Sense. Namely, Earth is expected to move in some direction. If light is moving with velocity c in every direction in Absolute Space (what else?) then in the direction of the motion of Earth it seems to move with c-v in an Earth laboratory, while with c(1-v²/c²)^1/2 in an orthogonal direction (no proof here). So it seemed that there remained only 2 possibilities after the negative result:

1) For any reasons light propagates with constant velocity just with respect to Earth; or

2) For any reason Earth almost stands still in Absolute Space.

Now, 1) was too similar to the old picture of Ptolemy ("Earth is the true center...") and 2) needed a miraculous cancellation amongst many motions (Earth orbits Sun, Sun orbits the center of Galaxy & so on, and the result is zero just by pure luck?). Then for 20 years various explanations were invented but then always turned out that the explanation was even worse... Then came Einstein, from the other end. He told: we have measured the velocities. We have obtained that it is the same in each directions. So this is Nature. Light travels with the same velocity in all directions in each inertial system, so in a group of systems moving with constant velocities with respect to each other. Is it contradicting Common Sense? Bad for Common Sense but this is Nature. This can be true if not only space coordinates but also times differ in different coordinate systems,

Einstein then formulated the transformation; that is the Lorentz Transformation. If time differences ("durations") and space differences ("distances") between the same 2 events transform so between different observers moving with different but constant velocities, then Light is travelling with velocity c in vacuum for any observer moving with any but constant velocity. (For details see e.g. Vizgin, 1981.)

Why? Why clocks "are slower" on a rocket moving with great velocity? The answer is that they are not slower. The clocks on a rocket have the same mechanics as clocks on Earth. True, when they are measuring the time interval between two events (say, two light sparks) they measure less time between; but they are not on the same place either. Even if the rocket was at Earth at the first spark, it must have gone away until the second, being its velocity different. Then what? On Earth a minute passed between seeing two sparks, on the rocket fortyeight seconds, what is the problem?

But why? Indefinite question. Einstein did not know the answer and was not too interested. Nature works in this way; this is a natural law; he was no philosopher. In 1908 came Minkowski, and showed that the Lorentz Transformation is a rotation in the 4 dimensional Minkowski space, whose coordinates are the space coordinates (3) and time (1). Different observers see different distances and time intervals between 2 very near events, still the proper distance ds

(2.1.1) ds² = dx² + dy² + dz² - c²dt²

is invariant, same for everybody.

Then: has the Fourth Dimension been found? No. Time is not the fourth dimension of space but that of space-time. Time is different. Look, the proper distance of two events connected by light velocity motion is zero! The proper distance of different things, maybe even not feeling each other may be 0! The Minkowski Space-Time is not Euclidean but pseudo-Euclidean. Because of this, between 2 events the straight path is not shortest but longest. Nature is such.

And back to happiness and naivity. Einstein is happy; Einstein (geborene Marity) too. No surprise: this is a big thing and journals start to write bombastic articles. But the construction is impossible. Different observers measure different things (no problem), but data of physical meaning are the data invariant between two observers (good). Invariance holds only among observers performing motions of constant velocity with respect to each other ("inertial motion"). But how to select the first observer?! If she is a piruetting balerina, the others will rotate too. With respect to each other all will move with constant velocities, but Lorentz Transform is not proper to the stories seen by them.

To be sure, Einstein is concentrating on the problem from 1907 (Vizgin, 1981). Without success until 1913: the proper tool, Riemannian Geometry, is at another ex-co-student born in Hungary, Marcel Grossmann, whom he meets again in 1912, This step is very important, but will not change dimensionality directly.

Let us continue, but still before 1913.

Light is moving with light velocity, i.e. so that proper distance (2.1.1) between any pair of events on the same light path is 0. All the light paths starting from an event E constitute the future light cone of E. All the light paths going into E are the past light cone of E.

Let us make an axiom: all possible physical motions are either inside a light cone, i.e. ds²<0, or on a light cone ds²=0; no motion crossing the light cone (ds²>0) is possible. If this is true, then a motion cannot turn back in time, and if E is before E' for one observer, it is before for all of them. If the axiom is true, time machines are impossible. Good, because indeed we do not see such anomalies. Why ds²>0 motions are impossible? Who knows? Nature is such.

Time travels lead to paradoxes. (One does not like life but is reluctant for suicide; then goes back to prevent his father and mother meet. Will the time traveler vanish from World? Then who prevents the would-be parents to meet? See also the story of Oedipus Rex.) So Law and Order is guaranteed by the simple local rule

ds²>0 is impossible.

I will call this rule local causality. But problems will come back later.

Now, are we really sure that Space-time is of 4 dimensions? What if it is 5 dimensional, and the Fifth is also time-like, only clocks do not feel it?

Then, probably, we also do not feel it. At least our biology does not feel it, since ageing is not too different from entropy growth, and clockwork. Our psyche or spirit or mind may feel it, for our ignorance about psychic processes.

Let us call the second time coordinate q, and let us choose the second light velocity also c. (This is only a matter of definition for units.) Then

(2.3.1) ds² = dx²+dy²+dz² - c²(dt²+dq²)

But then consider a body moving only a bit in t but much in q. For ds²<0 then a lot of motion is permitted in x, y and z, the body moves a lot in x and only a little t is spent (measuring apparatuses do not observe q). For another observer this story might seem even as dt<0. So, if we see strict causality, no time machines &c., then we can be sure that there is no second time-like coordinate of space-time. Still n=4.

It is not against causality to imagine a fourth space-like dimension, which I will call w. However we do not see it. (Special) Relativity does not like situations when light cannot propagate; the whole theory started with light signals. So either something new has to be invented instead Relativity or one must give an explanation why we do not see the fourth orthogonal in the corner of ceiling. We shall be able to return to the problem in Chapter 3.2.

Riemann Geometry was invented by Riemann, following Gauss, in the middle of 19th century, and for 60 years was known only by a few architexts, colourists and mathematicians.

The idea is simple, and I must tell it not only because General Relativity is my favourite topics, but mainly because of the needs of Chapter 6.

Consider first a surface. On it each point can be labelled by two coordinates which I will call a and b. If the distances fulfil some simple relations which I will not discuss (but triangle inequality is one of them), then for 2 infinitesimally nearby points

(3.0.1) ds² = f(a,b)da²+2g(a,b)dadb+h(a,b)db²

where f, g and h are coefficients to be measured. To be more elegant and general

(3.0.2) ds² = g_rs(x)dx^rdx^s

where now

(3.0.3) x¹=a, x²=b

and if an index occurs twice, above and below then there is automatic summation for it. This is the Einstein convention. Riemann geometry requires that the metric tensor g_ab be positive definite; then the distance of two points will be always >0.

This is the situation on every curved surface. For example, if we use the longitudes and latitudes of geography, then we get the form (0.5), and we never can transform it into the Pythagoras Law. A surface is curved if the metric cannot be transformed (by choosing proper coordinates) into the Euclidean g₁₁=g₂₂=1, g₁₂=0. The mantle of a cylinder can be transformed so, the Pythagoras Law is true on the mantle of the cylinder, so the mantle of the cylinder is not curved. Sorry.

Is it possible in higher dimensions? Yes, why not?

This is General Relativity, but maybe you would not be too interested. So only briefly.

Einstein & Einstein returned from Prague in 1912 and started to quarrel. So the male Einstein got more free time and started to discuss with old friend Grossmann. He told him (E. to G.) that he would need an absolute calculus in space-time and then he could use any 4 coordinates. So then he could transform between observers moving accelerating with respect each other, or one piruetting or anything. Reality should be independent of the observer; he is only observing, not influencing.) How to manufacture this Absolute Calculus? Then for his surprise Grossmann told that the absolute calculus exists, called Riemannian Geometry, and he is teaching it. So they sat down and applied it on space-time (Einstein & Grossmann, 1913).

The task was not quite trivial. The Minkowski space-time is pseudo-Euclidean so now instead of Riemann geometry a pseudo-Riemann one will appear. Nevermind.

And: what governs the metric g_ik? Einstein solved the problem in 1916, in Berlin (without Grossmann and the other Einstein, who remained, separately, in Switzerland). He wrote down the Einstein (or Einstein-Hilbert) equation. The curvature of the space-time is a tensor; some combination of this tensor is proportional to the energy-momentum tensor of matter. This is Gravity: the proportionality factor is -8pG/c⁴, where G is the old Cavendish constant. But I stop here. This text is not about General Relativity. Only remember: distances do not have to follow Pythagoras Law.

Local Causality remains as it was. If g_ik is "pathologic", time travel is possible and then FTL too. Maybe this will be salvation of Humanity. Or somebody can change our past and then we vanish. Or, maybe, such spacetimes are impossible, via mystic Cosmic Censorship. These problems are deep and important, but does not belong to the present topic. I wrote this paragraph only to demonstrate that I could write something about Time Travel too. With my own hand I was able to get acausal solutions of the Einstein Equation, but in my profession that is regarded rather as bad luck. Enough of this.

Now we can make constructive statements about the extra dimensions. As we saw they cannot be timelike. They can be spacelike. For simplicity, assume that there is one such, the mystic Fourth. Then it must be small, because it cannot be seen. But it can be small. Imagine that Space is curving back in Fourth Dimension just as the mantle of a cylinder. (It is curving back, but does not become curved. English Language is older than General Relativity.) And the thickness of the cylinder is microscopic, say 10^-13 cm, or Planck length. Then there is a Fourth Dimension and still we cannot see it. No contradiction. The extra dimension appears in the Einstein equation, but the influence may be weak.

I have a paper (Lukács 2002to appear) about the n=5 problem in a Volume just at the publisher and I do not want to break copyright. However I have some older papers. So I tell that microscopic extra dimensions would lead to slight apparent violations of the Equivalence Principle (Lukács & Ladik, 1993). Now, Fishbach & al. (1986) believed to see such anomalies, maybe proportional to hypercharge. Also, it is often believed that Electromagnetism comes from the extra dimension; we have proven (Lukács & Pacher 1985) that it does not.

Still, shortrange and/or weak interactions may be caused simply by motion in extra dimensions, compactified at small sizes and so not seen. A lot of particle physicists like 10 dimensions for space-time; 6 compact. That is supersymmetry. A minority believes in 26 dimensions. Once I heard a lecture about n=306. Recently a theory works even with indefinite number of dimensions.

But in all above the 3+1 familiar ones the space is as a thin torus, cylinder, doughnut, membrane or such. And then we are at a situation discussed at the end of Part 0: the extra dimensions are thin, so it is hard to see them from distance measurements. On long range such a space seems 3 dimensional.

And now we can at least try to formulate a way to answer to the question: why just 3? The Universe expands in 3 directions. Why? Because the solutions of the Einstein equation are such. Now applying the equations in 4+1 dimensions one can get a solution expanding in 3 space directions, contracting in 1; indeed the simplest solution is such (Chodos & Detweiler 1980; Chodos 1984). Then the story goes: space is indeed of 4 dimensions but World is old and one dimension has shrunk beyond visibility.

Still 2 questions wait for answers. First: why just 3 dimensions remained big? Was it a sheer luck or was it necessary? And: we cannot write the proper equations, because we do not know the forces in extra dimensions. That belongs to particle physics and work is going but time is needed. If the extra dimension were responsible for Electromagnetism, then in 5 dimension we could simulate the growth of electric charge and decrease of G in the very youth of Universe (Chodos & Detweiler 1980). We tried it, but it did not go. In such a scheme the electric charge cannot grow to the present value (Lukács & Pacher 1985; Pacher 1985). This is the reason that I told, Electromagnetism does not come from Fourth Dimension, in spite of Clarke (1956)'s ingenious novellette.

So far the actors were point-like "particles". The location of a point is simply its place. OK, we have 3 dimensions of usual space, unknown number of microscopic others, not discussed henceforth, and one for time. But it is not simply so if the actors have internal structure.

The ideal dumb-bell is two point-like particles, say, of equal masses M/2, joined together via a rigid rod of length L, with negligible thickness and mass. Then the position of the dumb-bell is determined by 5 spatial coordinates: the 3 coordinates of the center of mass, and two angles for the direction of the rod. So the motion of the dumb-bell is elegantly handled in 5 dimensions, 5+1 if relativistic. (I do not write equations when it is not absolutely necessary, because equations are clumsy in HTML.) Now, is space 3 dimensional or 5?

I am not going to answer. I have given the barebones of necessary information. If you are interested, think about. The question is more philosophy than physics. Read Bishop Berkeley (1710); he discussed the problem.

In Quantum Mechanics (QM) the particle is not a point but a probability function Y(x,t). Y gives all information about the particle, e.g. Y(x,t)Y*(x,t) is the probability to find the particle at place x in time t.

OK. And if we have 2 particles? For example a H atom is a proton and an electron.

In first approximation we may consider the proton infinitely massive; anyway, it is 1836 times more masssive than the electron. An infinitely massive proton does not do anything else than attract the electron. But in second approximation the situation is similar to the dumb-bell. A H atom is described by 2*3=6 coordinates. After some mathematical juggling 3 coordinates go to the center of mass and in these coordinates the atom does very simple things, another 3 are the "relative coordinates" and the cloud of the single electron can be investigated in them.

Now consider a He atom: a nucleus and 2 electrons. OK, let the nucleus be infinitely heavy and forget it. Still, the 2 electrons mean 6 space coordinates. Really

(4.2.1) Y = Y(x1,x2,t)

i.e. probabilities depend on the positions of both electrons, since they interact. With more than 2 electrons Pauli principle appears too. You cannot put 2 electrons into the same quantum state. Spin-up and spin-down are different quantum states, but 2 spin-ups "cannot occupy the same place". This principle appears in the form of Y.

One can make Quantum Mechanics in 3 dimensions, still it seems as if the system existed in 3*N.

And then what if we want Relativistic Quantum Mechanics? Does the helium atom live in 8 dimensions or in 7?

Y = Y(x1,t1,x2,t2) or =Y(x1,x2,t)?

The answer is double. First, Relativistic Quantum Mechanics does not exist as a full, self-consistent theory. Quantum Mechanics does exist, only it is not true because of Relativity. Relativistic Quantum Mechanics is not a closed theory, it cannot be made closed, and the true theory is Quantum Field Theory. (Only that gives disturbing infinities, removed by working but nasty renormalisation; so let us not discuss.) Second, as far as we remain at approximations, 7 dimensions seem better than 8. Draw any conclusion you like.

In 1980 a colleague of mine, from the same office, produced a generalisation of General Relativity (Sebestyén, 1980). He took 2 mass points in space-time and tried to write the Einstein Equation first in 8 dimensions, then only in 7. He solved the equations, got a motion in many dimensions and interpreted it.

In 8 dimensions the solution was rubbish. Either the theory is bad, or there are not 8 dimensions. But in 7 dimensions, projected into 2*3+1, there seemed to be cca. an elliptic motion around each other, with periastron precession and such. The picture was at least promising, but it could be checked only on double neutron stars, rarely observed. Unfortunately the colleague lost his interest then in this problem.

Again, you may draw your own conclusion.

Bishop Berkeley, younger contemporary of Newton, attacked Mechanics from another angle (Berkeley 1710). He imagined first a lone observer in Space. Assume that the observer is a structureless point (now I ask all Indo-European and Semito-Hamitic readers if a pointlike observer is he, she, or it?), still able to observe. Now he cannot tell if he is moving on straight line or not, accelerating or not, because there is no reference point. Two observers (or one and a lifeless point) can decide if they are moving apart or nearing, or orbiting, but nothing else.

But with 3 points 2 can orbit each other. Then the observer can use them as a clock and can somehow measure his distance from them &c. So mechanics starts from N=3 (n=9?) but first maybe not Newtonian. (We in 2002 know that n=9 is not enough. To measure distances some other point particles are needed, e.g. photons. Nobody has worked out this exactly yet.)

Later Ernst Mach developed this idea further (Mach 1883). At him there are infinite many bodies in the infinite Universe and by long range forces this jungle of bodies generate masses for each other. If you remove them, masses vanish. The lone body has no inertia, so can move as he (?) wants. As Berkeley has shown, it is impossible to forbid him, anyway.

In this picture Space, Dimensionality &c. seem to originate from the bodies and not simply bodies exist in a Space. What is interesting, the theory is not simply philosophy; it can be formulated as an alternative Mechanics (Barbour & Bertotti, 1977), and in roughest approximation the predictions are not absurd.

This work is not finished, draw your conclusion.

In a later version maybe I will write a lot of this. Now only note that in Thermodynamics the state of the system is described by extensives, as Volume V, Energy E, Particle numbers Nⁱ and such. If this is the variable set, then the thermodynamic potential is Entropy S, depending as

(5.0.1) S = S(V,E,Nⁱ)

But you can exchange S and E, or can substitute some extensives with the respective intensives or both. It is necessary to note that S is homogeneous linear function of its variables, so

(5.0.2) S = Y_IX^I

(5.0.3) Y_I =¶ S/¶X^I

Now Einstein (1910) observed #5 that in some approximation the thermal fluctuations can be calculated from the entropy function. First observe that according to Planck (1900) for the number of microstates W belonging to the same macrostate

(5.0.4) W ~ e^S

Hence, by some acrobatics, he got

(5.0.5) <dx^Idx^K> = g^IK/V

where dxⁱ is the fluctuation in extensive densities E/V, Nⁱ/V &c.,

(5.0.6) g_IK = ¶2s(x)/¶x^I¶x^K

(5.0.7) s = S(V,x^IºX^I/V)

and g^IK is the inverse of g_IK

Now, these formulae resemble some of Riemann geometry, and indeed it is possible to manufacture the Riemannian Geometry of the thermodynamic state space (Ruppeiner 1983, Diósi, Forgács, Lukács, & Frisch 1984, Diósi & Lukács 1985).

The dimensionality is as the number of independent extensives minus 1.

There is just some work in this topics, I just started some work too, so I think I shall later upgrade this Part. But let us write something just now.

Some ancients believed that there were 3 "primary" colours: white, red and black; a lot of tribal people used these 3 colorants and no more; also Mehta (2001) states this for Rigvedic Indian texts.

Strangely enough Aristotle (-60b) writes, at Bk numbers 373-379, especially at 374^b, that all colours are mixed from white and black; but he does not tell how. Maybe this was simply an idea and then he was unable to elaborate. According to Mehta (2001) Zarathushtra told the same, contrary to Daeva-worshipping Brahmins. Still in the beginning of 19th century Goethe told the same. These ideas were not operative.

Operative theories started with Newton (1704), Palmer (1777) and Young (1802). They assumed some primaries and the others they regarded as mixtures. In the 19th century on the British Isles the idea was that something in the eye reacts to primaries; the question was their number.

Then came Maxwell. But first I note that in the time of Maxwell women did not appear on university departments, except as cleaning women and they did not socially mix. Even secretaries were all-male.

Maxwell demonstrated in a reproducible way that he could reproduce "all" colours by using 3 lights, red, green and blue, only the relative weights should have been changed. (The quotation marks indicate that he was unable to reproduce very bright hues. But maybe his colours were not pure.)

Then the number of primaries is 3. The eye can react in 3 different ways. All mixed colours contain mixtures of these three, the eye measures the mixing coefficients and send them to the brain.

Colour photography and colour TV work on these ground and they work indeed. The theory must be at least approximately correct. Is colour space 3 dimensional?

Later came distance measurements. If you can reproduce a colour via the sum of 3 lights with some weights, then you can make a slightly different one too with slightly different weights. Then the observers were asked to produce the just distinguishable hues. Let the just distinguishables be at distance 1 (or anything), then with a lot of work the geometry of the colour space (the metric tensor g_ab) can be measured. It has been (MacAdam, 1942) and it is not Euclidean.

And, while this space exists "only" in our brains, it is objective in the sense that it is the same in everybody's brains. With two (?) exceptions.

1) Some people "see" all distances smaller, some bigger, but proportionately. Maybe this is only the degree of experience to discriminate. A wall painter has learnt to distinguish nearby hues; laymen are not interested in fine details.

2) Persons of "abnormal" photoreceptors (e.g. daltonians) have different spaces. We shall to return here later.

But otherwise colours of different persons live in so similar spaces that measurements can be summed up to survey the Human Colour Space.

Parallelly anatomy looked into human eyes and found two kinds of visual receptors: rods and cones. Rods are very sensitive with a shortwave maximum; cones are not so sensitive, with longer wave maxima, 2 or 3 types. The leading idea became: rods are for nocturnal vision and do not participate in colour impression, and the 3 different cones yield the 3 data of colour for brain. If you excite the 3 rods in the same way, your brain always observes the same colour. This is the reason for 3-dimensionality.

Weinberg (1976) explained why the colour space is curved. Briefly: the evolutionary meaning of colour vision is recognition of surfaces under changing but natural illumination. The curvature is a byproduct.

In 1988 I made a minimal analytic model with Gaussian sensitivity curves (Lukács, 1988). (They are really quite Gaussians at middle wavelenghts.) In one direction (neutral amplification) the metric is almost trivial; on the two dimensional surfaces of equal luminosity the geometry is of Bólyai-Lobatschevsky. But now we are interested in dimensionality.

On the basis of the Weinberg (1976) theory the answer is simple (Lukács, 1988). The brain fits theoretical curves to the observed signals. With 3 receptors (3 fixed sensitivity curves) it can fit 3 parameters, say, albedo, location of maximum, width of maximum; Gaussian parameters. The importance of the first 2 is trivial; for the width I note that a wide Gaussian can mimic the sum of 2 Gaussians and natural colorants with 2 maxima are frequent. 2 parameters are not enough; 4 may be better, but perhaps the gain would be only moderate.

On the other hand really it seems to be 3; we seem to be quite satisfied with 3 dimensions, so it seems evolution was too. Colour TV & movie work with 3 stimuli. People always criticise TV, but they generally tell that colours are distorted (and often turns out that the apparatus is incorrectly fixed), not that they are deficient.

When people speak about colours, the situation is rather obscure. Women amongst themselves tend to use individual colour names coming from fashion, fantasy names of cloths &c.; men among themselves simplify the colours (a man's shoe is simply brown) and in mixed company men avoid to discuss colour topics with women. However when people try to eliminate emotions, it seems that at least in the European culture the following approximation is not bad.

1) The surface can be luminous or not. This is roughly albedo.

2) There is a dominant hue, say: yellowish green. This is cca. a wavelength, cca. 550 mm.

3) Is the colour pure or diluted (pastel)? This means cca.: there is a dominant hue, so a pure spectral colour; how much diluting white produces the actual colour?

Then a "dirty greenish blue" means a spectral turquoise, diluted a lot and not very high albedo. There is no evidence for more than 3 parameters.

If one cone type is absent, the individual is daltonian, with n=2.

Now, if we indeed have 3 different cones plus the rods, then the brain gets four data! Why our colour space is not 4 dimensional? Or: is it not 4 dimensional?

It should be, and it seems that it is not. An explanation is that our brain suppresses the rod data in daylight. Namely, in transitional hours the reported mixing weights would change. (See the Purkinje effect.) Then colour constancy would be violated, and the observers would be confused. (Some persons indeed are then confused!) Maybe some congenial painters reproduce the suppressed dimension, and then they sometimes impress some observers. Maybe.

The problem has not been sufficiently investigated with the necessary objectivity.

Pectens are dumb shellfishes. All shellfishes are rather dumb, which is not strange, because in Evolution their heads have been lost. (In the most primitive living groups still some remnants of the head are retained, as on Nucula nucleus) Pectens have cca. 40 different receptors.

According to newest results birds have 4 receptors (Palacios & al. 1990; Fager & Fager 1981; Varela, Palacios & Goldsmith 1993; Anon 2000). It seems that they go back to a more primitive dichotomy, a shortwave and a longwave one, and the 4 is a second stage, although the picture is still unclear (Anon 2000).

Again, birds and we had common proto-reptile ancestors before 310 Ma (Kumar & Hedges 1998). Had they colour vision or not?

From recent data it is possible, that they had 2 receptors, and the next stage of evolution happened independently on the diapsid (dinosaurs + birds) and synapsid (therapsids + mammals) branches. Anyway, it is possible that our night vision (rods) is related to the shortest wave bird receptor. However take into consideration that mammals "in the shadow of Dinosaurs" probably retired to night life, in which case mammal colour vision restarted on the K/T boundary (Holba & Lukács 1995).

We can live with mere 3 receptors since our brain is big and can calculate the parameters. Pectens do not have even heads, so they must use raw data, therefore they need a lot of receptors.

Now, this Chapter will be very short first, because we just started to work here. But: recent data seem to suggest (Mollon 1992; Zorpette 2000; Hambling 2001) that a minority of women are tetrachromats (4-dimensional). Theoretical explanation: maybe a gene for a paint has two alleles. If this gene is on Chromosome X, then women, having 2 X's, can have 2 similar but still different receptors at the place of men's one.

And now back to Maxwell. If the above picture is true, some women (minority) possess richer colour space, some differences not seen by either men or majority women. Then a minority of women may see that colour reproductions (TV, movie, &c.) are incomplete; but they are ignored.

Now you can see why I mentioned that in the time of Maxwell's successful 3-light demonstrations even secretaries were all-male.

As experts know, at the end of 2001 the governing "party" of the Western Cape Parliament (South Africa), Democratic Alliance (DA) got to the brink of breaking into two. No doubt, they will split and they are only waiting for technicalities of the divorce. I guess they will practically form the original components Democratic Party (DP) and New National Party (NNP), still legally existing in both the SA and the WC Parliaments but not in Cape Town Unicity. Of course, it is not my task to comment the step from political viewpoints; we know that there were some internal struggles of Tony Leon, leader of DA/DP and Gerald Morkel, Provincial Prime Minister on one hand and of Marthinus van Schalkwyk (the "Kortbroek"), leader of NNP and of Peter Marais, Metropolitan Mayor, on the other. The personal conflicts are irrelevant here. Also, we know that some purposes, tactics &c. of the two sides differ. Of these as much is relevant here as is connected with the dimensionality of the space of party politics.

Also now we can know that the revived NNP made a coalition with the biggest party of the republic which is now going to be first also in Western Cape, the African National Congress, ANC. Obviously, smaller parties often want to go to coalition with big parties (often unsuccessfully), so this is a political move and does not have to get an explanation in Riemannian geometry.

But there is something belonging partially to Riemannian geometry, and that is the possible future of DP and NNP. Of course, I do not mean prediction. Such predictions are very uncertain, and cannot be verified until 2004. But I do mean the question whether in principle there may or may not be some places for both. The first answers of the analysts were rather negative.

We shall see that the Western Cape situation has some Hungarian analogies. So a few words about the language of Hungary. I guess, international analists speak even less "Hungarian" (really Magyar, see later) than Afrikaans; Afrikaans is at least Indo-European and in fact quite a close relative to English. Therefore they get comments from Hungary in English, as they get them from Western Cape. But English-speaking people are not necessarily the average people.

Up to now, the Riemannian structure of political space has not been found. However I think it exists. I give here a semiquantitative proposition, but do not try to work out just now. Two parties in the Parliament are near if in most cases they vote together. In Germany, in the last 40 years CDU and CSU voted practically always together, and indeed they are handled almost as a single party. If one needs distance data, he can start with a measure of common voting as an "overlap integral". If they always vote together, distance is 0, if never, it is ¥. In between, such a calibration is needed which is compatible with triangle inequality and such.

Another point is the manifold of supporters: if voters can go to and fro between 2 parties, maybe they are near. But this criterion rather measures distances at election.

England has the oldest continuous Parliament. The Lower House, or House of Commons was always elected, back to 13th century, and the English system is to choose 1 (one) from any number of candidates. Such a Parliament is not "proportional".

When nationwide parties appear (in the tumultuous 17th century in England), such an election system prefers 2 parties. For example, one in power, who tells that things are quite good and should leave it unchanged, the Conservatives; and one wanting to replace them, to oust them from office. If they are successful, then the conservatives try to return; with the slogan that they are defending the good old times of natural ways.

This remained so in England (Britain) until cca. 1900.

Now let us see the origin of the expression Right vs. Left. That is a collinear arrangement coming from revolutionary France just after 1789 and shows the seats of the respective group in Parliament.

The Right wanted to conserve, Left to change, as above, and middle groups told that changes are necessary but with caution.

When the French Parliament voted about the fate of King Louis XVI, there were middle groups voting for execution with some conditions. However it was quite easy to locate each Convent member along one line between Yes; Kill Him and Throw Into the Lime-Pit, and No; Do Not Dare, Rather Kiss His Holy Foot. Of course, in one question there is always a Yes or No. But the collinearity was quite common. Friends of King were also for the Catholic Church, were for the feudal system, and so on, and friends of Citizen Robespierre, the Virtue and such for just the opposites.

Both in England and in France the composition of the Parliament remained more or less unchanged during the 19th century. One conservative party, the Tories, and one liberal, the Whigs, in England/Scotland. A royalist/ultramontane pole in France, a republican/freethinker (or atheist) in France with transitional groups in between.

Now, observe that in the 19th century voting right was not general, except some states of the US, where all adult males might vote. (Women's voting was not taken seriously.) Everywhere in Europe there were some limitations. In the West limitations were for income or property. In the East nobody elected anybody. In Hungary first noblemen elected, and then all noblemen plus commoners with some income/property. (In Eastern Central Europe, Poland-Lithuania and Hungary-Croatia, noblemen were a strong social group, some 10% of population; see an analogy with Apartheid South Africa.) And came the Industrial Revolution. In England already in the 18th century, on the Continent during the 19th.

And the Industrial Revolution distorted the society. When Karl Marx and his fellow Communists wrote the Communist Manifesto, it seemed clear that the process will eat up the old society and produces something quite new. A host of propertyless but disciplined men was being produced, who worked in big groups in factories, performing the hour-to-hour machine-like tasks of Early Industrial Ages. At the end all of the society will be composed (everybody believed) of a small minority of command-givers, and an overwhelming majority of rightless workers. And then why not to oust the command-givers?

Step by step new groups achieved political rights, and in the Parliaments a third group appeared. They were representing the workers of Industrial Age. For them the relevant questions were not King vs. Parliament, or State Church vs. Presbyterianism, or Religion vs. Atheism, but the right to form trade unions, the length of working day, or the right to take away property.

But this means that henceforth political argumentation and coalition-making could go not on a line but in a triangle. There appeared a Third Way. You could opt for State Church as a Tory; or for Methodism, Quakerism, freethinking or such as a Whig; or for trade unions. You could go right (Tory), left (Whig) or up (Socialist).

For a physicist, however, this is only two directions: horizontal or vertical. Right vs. Left is not two directions but one; with positive or negative sign. Two Extremes or Poles is 1 dimension. But three Poles is already 2 dimensions. Generally, n poles mean (n-1) dimensions. The simplest body in 3 dimensions is a tetrahedron with 4 corners.

In Europe Socialists became substantial powers in Parliaments more or less at the beginning of the 20th century. For a short time it seemed that genuine tripolar politics would start. Also, it seemed that with full and equal voting power ("one man, one vote") Socialists could lick all others together. This, at the end, did not happen, because came the even newer idea, Rights for Women.

One woman, one vote existed in New Zealand then; other countries applied limitations. They gave the voting rights to women able to write; or head of family; or with maturity examen. And then again, more and more women got the rights.

Taking Hungary as an example, before the First World War less than 10 % might vote: only men, all noblemen plus city middle class, farmers with land enough to live from it, and village brain-workers. In 1920 a lot of women got the right, but it was again reduced in 1922. In the 30's the system was nearing one man one vote, with a lot of voting women. In 1945 in principle voting power was total.

The 20th century was complicated in Europe, and the Second World War made a caesura in many countries. Not in Britain; there elections went regularly during all the century, so we can learn something. For example just now Left Labour has a large majority in Parliament. If all politics can be described on a line ("Left" vs. "Right"), then the true opponent of a definitely leftist party is a definitely rightist party. If, in addition, the election system is British, with districts delegating only one member to Parliament, then generally only 2 parties can really succeed. Except if the country is inhomogeneous. Then at one part of the country parties A and B concur; at another part A and C and so on. An example is Australia. In recent years Labour is strong everywhere, but in cities the opponent is the Whigs and in countryside the agrarian National Party.

Still, there are generally more than 2 substantial parties. In Britain, e.g,, there are 3 nationwide (?) parties: Labour, Tories (Conservatives) and Whigs (Liberal Democrats). The question mark is meant for the doubt what is "nationwide". For example Scottish is a nation, Scotland has her own regalia, there Elisabeth I rules, and there is a Scottish National soccer team participating in Europe and World Championships. And there is a Scottish National Party. But let us remain at the 3 big ones.

Since Maxwell's 3 colour theorem holds (doubts about some women were told in Part 6), the space of colours is of 3 dimensions. Let us ignore absolute luminosity; then we remain with a surface, on it with the colour "triangle". This space is spanned by 3 fundamental colours which do not exist but can be approximated by Extreme Red, Extreme Blue (not violet!) and some vivid Green.

Then: what is the contrary of Red? In some sense this contrary does not exist. If something is very non-red, if it does not contain any red component, still it can be green, or blue, or any greenish blue. Of course, there is only one hue giving neutral white or gray with red and that is turquoise, but if one knows only that he does not want to have any red component, then he can be green, blue, or combinations.

If British opposition were fanatic to replace red Labour, that could be made easiest way by an alliance of green Tories and blue Whigs. However this coalition did not exist except national emergency in war in the last 75 years.

In Italy there were no elections between 1925 and 1945. In the 50's the election system was strictly proportional, resulting in chances of middle parties. There were 2 and only two real political wings, dictated by Cold War. The Right, mainly the Christian Democrats, was friend of the USA, the NATO &c., honoured the Pope, opposed the divorce & abortion, &c. The Left, mainly the Communists, was against the NATO, hoped in the Soviet Union, and fought for freedom of women. Still a lot of middle parties lived quite well, going from right to left the liberals, who supported NATO and USA but did not oppose divorce and abortion, then the Social Democrats, who wanted serious economic changes for workers but still supported NATO and USA, then Socialists, who were definitely for NATO but not very much for USA, ending with the Socialist Party for the Unity of Proletariat which, maybe, wanted to build Italy's own Communism without Soviet Union. (This had been accepted later also by the Communists.) Each hue reflected somebody's opinion, so all these parties got some votes and so some seats. But the two biggest were the two extremes. Also in Netherland and Finland the proportional systems produced multiparty governments. In 1963 the Second House of the Parliament of Netherland was composed of 10 parties; for a majority rightist coalition 3 big parties were needed. In 1966 the Finnish Parliament had 8 parties, of which 4 formed a left-center government. In later years Finnish government coalitions generally included the Party of Swedes in Finland: almost all Swedes vote for this party, it gets some 6% and so it is not easy to leave it out.

Germany took another way. The German electional system is almost proportional; except that it does not permit any party to the Parliament below 5%. The result is now a 6-party Parliament, with a big Left party (Social Democrats), 1+1 big Right ones (Christian Socials in Bavaria and Christian Democrats everywhere else), a smaller leftist party PDS on the East, and two in between, the Free Democrats or Liberals and the Greens. Just now the Social Democrats and the Greens are the government, the PDS the leftish opposition, the CDU, CSU and FDP the rightish opposition. But note that 2 of these parties come from inhomogeneities. In a West Germany minus Bavaria there would be no PDS and CSU.

It seems that 20th century produced tripolarity. If so, we can use primary colours, red, green and blue. Then the Parliament (or the country's opinion) can be characterised by a single hue, from which you can see all the ratios (if you have the experience of a wall painter). Now, I collected the composition of German Parliament from 1903 and 1912; then from a lot of elections until 1933; and then from 1949, for both Germanies (East Germany is an insert). They can be seen on Fig. 1. The last, unmarked, square is 1990.

Fig. 1: German elections. Henceforth Red is "Socialist" (in general sense), Green is "National/Conservative" and Blue is "Liberal".

Before 1914 the Conservatives and Liberals dominate. After 1918 Socialists and Conservatives. After 1945 Conservatives and Socialists, although Liberals still exist but they are not strong. Maybe the political space is narrow in the liberal direction? Liberals were stronger in East Germany than in the West; but there were no real elections.

Now I give all Hungarian Parliaments from 1866 to 1990, when real elections happened at all. Before 1949 and 1971 people might vote only for a single list, which they obediently did. In 1971 the British system was adopted but without the right to nominate candidates. It was theoretically possible from 1980 and indeed sporadically happened in 1985. As for the 1994 & 1998 parliament wait a minute. (Next election on April 7, 2002.)

Fig. 2: Hungary, 1865-1990.

First you see something similar to Germany. Before First World War, Liberal/Conservative struggle. After First World War Liberals almost vanish. We can try with theories, but it is not the task of a physicist.

After the Second World War this tendency continues until free elections cease in 1949. But Liberals return in 1990. In the 1990 Parliament Liberals dominate the opposition.

And in the next 4 years in most cases the bluish purple Opposition opposed together; but in a substantial number of cases either Blues or Reds supported the government. (For some questions 2/3 is needed as in Germany or in South Africa between 1994 and 1999.) The Blues were not simply Middle between Green Right and Red Left. The dimensionality of the Hungarian political space was 2; it was triangular or tripolar.

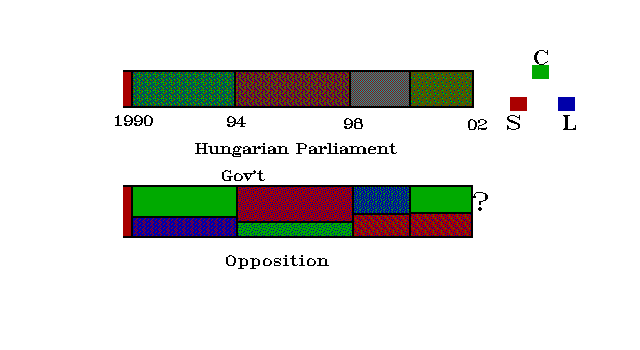
Fig. 3: Hungarian Parliaments, 1990-2002.

Then something interesting happens in 1994. Socialists have absolute majority in the Parliament (with 33 % of votes), they resurrected from utter ruins as the colours show, but Liberals are still strong. One Liberal party enters the government, another remains in opposition (both had the choice.)

In 1996 something happens, not seen on the picture. There is a party, MDF (Hungarian Democratic Forum) which was the biggest party in the 1990 Parliament with some 42 %. In 1994 the party collapsed, with less than 10 % of seats, but with this it was still the strongest Opposition party. Now, in 1996 almost half of the MP's of MDF formed a new party, MDNP, but the new party was indistinguishable from the old for colour, maybe the difference was for "style" #6. The new party remained without seats in 1998.

And in 1998 the smaller, opposition, Liberals become biggest party, and the bigger, Government, Liberals become small. So maybe it is easy to move between parties of the same colours. But in 2000 the big Blue party redeclares itself Green. Afterwards the Blue ideology is very poorly represented in the Parliament.

As for Hungary, this is the favourite question for politologists just before the elections. However, predictions of new Parliaments is not the business of a physicist, and, anyway, answers will come soon. In the campaign one party rallies with liberal ideas, however most goals seem to be at least parallel with those of socialists, so the campaign seems to be tripolar but only two-sided. Now we can turn to South Africa.

In any European country on the next election the second party has the chance to replace the now biggest party. In contrast, in South Africa even before the October 2001 Cape Town crisis the ANC dominance seemed impossible to question on republic level and in 7 provinces. Real struggle could be imagined only in KwaZulu-Natal and Western Cape, instead of Frederick de Klerk's hope and promise when he handled over the presidency after the 1994 elections. He told he would come back #7. Instead, after two more years he retired. His original party was reorganised but lost a lot of votes in 1999 #8. The liberal (and English-led) Democratic Party got votes of a lot of people NP voters before #9.

A brief analysis of the Western Cape crisis may show the problem. But let us see first some numbers.

In older statistics Blacks (=Bantus) were some 67 % of population, Whites 20 % (Afrikaans 12 %, English 8 %), Coloureds 10 % and Asians (Hindu & Chinese) 3 %. For now White ratio seems to have somewhat decreased, Black increased. (Natural growth, English emigration &c.) For languages, Afrikaans is the biggest language spoken by majority of Whites and almost all coloureds; English is, however, strong as second language between Blacks, White Afrikaners (but not Brown) and Asians.

In Apartheid times there were 3 substantial White parties. National Party was the party of anti-English Afrikaners. United party was first the party of everybody loyal to British Crown, later mainly English. Progressive Party was formed by liberals of the United Party. Then in the 70's United Party broke up, and the Progressive Party and other Liberals formed Democratic Party. In 1997 National Party was reorganised as New National Party.

As for numbers, in the White Parliaments NP was always majority. The first squares <94 are average compositions for White Parliaments and are rather symbolic. In 1983 PP was second, in 1987 Conservative Party, in 1989 Democratic Party. Now, on the first one man, one vote election in 1994 the African National Congrees got 63 %, NP 20 % and DP 2 %. Since another White/Afrikaans party got another 2 %, the traditionally White parties were at 24 %, clearly getting Coloured votes too.

However for us Western Cape results are more important. There ANC got 33 %, NP 53 % and DP 7 %.

In the next election, in 1999, ANC slightly increased the votes (seemingly from other black groups), NP (now NNP) got down to 7 % and DP up to 10 %. In Western Cape ANC became the biggest party with 42 %, NNP second with 38 %, and DP third with 12 %. It is theoretically possible that in Western Cape ANC won the extra 9 % just from NP + DP by the efforts of Patrick "Judas" McKenzie; however obviously NP's collapse was caused directly by DP's concurrence. But in Western Cape DP was little a concurrence. Peter Marais, in one of his election speeches, told the coloured listeners that they are the majority at Western Cape; "No one will govern us unless we say so... The NP is the natural home of brown Afrikaners -you must stand up and be the boss." (Heard & Paton 1999).

On the 2000 local election NNP and DP formed a consortium called DA. DA achieved very good results -according to possibilities. Note that in countrywide summation ANC got 59 %, DA was second with 22 %, Inkatha third with 9 %. Then Cape Times wrote: is South Africa "on its way to two-party state" (Rostron 2000) as US and UK (and maybe, Hungary?)? Rostron tells that: no; first Whites must give up the idea of White society. And he is of course right: a 22 % party is no competitor for a 59 % one.

Still, DA got the Cape Town mayorship (Peter Marais, Brown Afrikaner), the Western Cape government was DA (NNP + DP) under Gerald Morkel (also Coloured). Then on July 10, 2001 Morkel started an investigation against Marais, with the accusation that the mayor's office falsified signatures for a plan to rename 2 streets about presidents F. W. de Klerk (NP) and N. Mandela (ANC). DA replaced the mayor in October. Leadership of NNP was loyal to Marais and is going out of DA.

The first analyses predicted destruction for NNP (Calland 2001; Anon 2001a; Anon 2001b). The English-language articles tell that van Schalkwyk the "Kortbroek" has lost, (N)NP practically does not have any future after the split. (Note that Kortbroek, Short Pants, has equivocal meaning. It may indicate his youthful appearance; but it may mean too that he is a young boy in the struggle of grand old men.) Calland's article identifies DP as "English-speaking white" and NP as "Afrikaans-speaking white and coloured", and concludes that so DA had a faulty line inside. And he cites Marais telling: "Never, ever before, anywhere, has a coalition between Christian Democrats and Liberals worked".

And this definitely belongs to the present topic. Here Marais declares tripolarity in general.

On the beginning of November start to appear English analyses blaming DP leader Leon for the split. In an article of Forrest (2001) some citations appear for Afrikaans-English feuds. NNP councillor cites historic Boer president Kruger that British "...don't want the vote ... want my country"; and a White Afrikaner group tells that DA leaders "look down on everyone in the country except well-heeled urban English-speakers".

And then it turns out that maybe NNP is not yet dead. On Nov. 13 ANC suggests a law in Parliament permitting to change seats for councillors on party lists #10. And on Nov. 21 Marais accuses DA for being a "Pale White laager of frightened people". In the same time the NNP was his "refuge and pillars of strength". And: "we dare not break the strong bonds that have developed in the NNP between White and Coloured people nor lead Coloured people again into a master/servant relationship" (Marais 2001). Next day Marais tells that they are negotiating with ANC, and "When you negotiate with the DP you take all your lawyers so that you are not swindled. If you negotiate with the ANC, then you negotiate with people who have South Africa's interests at heart." (Sapa 2001).

On Nov. 27 the NNP-ANC deal is published and then Stober (2001) writes that "Marthinus van Schalkwyk is no longer 'kortbroek' -he has proven his political and leadership skills by negotiating the sweetest possible deal for the NNP as it enters into a co-operative governance agreement with the ANC". (And I ask: now how can Morkel (DA) prevent Cape Town Unicity Council to name neighbouring streets after Mandela (ANC) and de Klerk (NP)?)

Now, it is not the goal of this study to decide the political qualities of South African political leaders. However, I think that in October (English-speaking) intellectuals believed there would be no future for an Arikaans-based party; now it seems viable. Again, in October analysts believed that Socialism's opposition can be solely Liberalism. Now, there is a possible Conservative Pole too. Of course, only the 2004 elections can show how strong is each pole in the South African society.

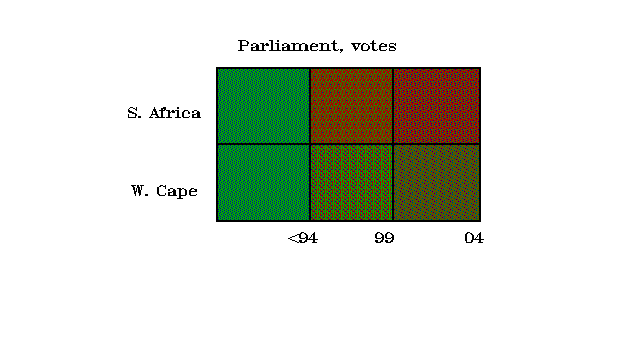
Fig. 4: South Africa, before and after Apartheid.

And now, instead of predictions, let us see the South African colours of Parliaments, Fig. 4. In Apartheid times the Parliament was all-white (however with 3 whites for coloureds); from 1983 there were 3 Parliaments for Whites, Coloureds and Asians. During all time the White parliament was predominantly conservative (and Afrikaans) with a liberal (and English) minority. Then came the multiracial elections. Of course it is not easy to classify all parties into a triadic scheme, but I applied more or less the methods I learnt in Hungary (Holba & Lukács 1990; Holba & Lukács 1994; Lukács 1993; Lukács 1994). If ANC is governing in coalition with Cosatu and SACP, it is probably Red. The successor of National Party must be Green. DP is often called liberals, so let it be Blue. UDM is more difficult, but General Holomisa comes from old Transkei Government. Meyer from National Party; Holomisa is for old Transkei, so Green. If anybody knows better, he may repeat my work.

I will not predict. In the Parliament of European Union there are 3 big groups: Socialists, Conservatives (called on various names in last years) and Liberals. Liberals are the smallest. In Hungary the Parliament had strong Liberal groups from 1990, now that is the smallest group, and we shall soon see the next 4 years. Is seems as if Liberals were nearer to Socialists than any of them to Conservatives/Christian Democrats/Nationals; but not in Australia, of course, neither in Japan. In South Africa the leading opposition party is liberal DP. The 1999 elections proved that Whites can almost freely diffuse between liberal DP and conservative NNP; and also, when the leading party redefined itself in Hungary, that was an indication that it is not hard to switch between Green and Blue. Still, it seems that Leon's and van Schalkwyk's possible supporters overlap only partially, but are not identical #11. In the Appendix I briefly discuss the problem of a notion which is not quite English, and so sometimes is called "nation", sometimes "volk", maybe "ethnos"; it is difficult but important for dimensionality because of group cohesion.

It seems that in this time in Europe, South Africa, Canada, Australia and maybe Japan the space of political opinions is 2-dimensional, but rather narrow in one direction. In USA practically there is no third pole, although in the beginning of 20th century even there started to emerge a red pole.

The origin of religions is an obscure problem, and does not belong to the present topic. I only note that there are two extremal theories: that originally people believed in One God and then the system became multiple, via e.g. cultural interactions; and that originally there was a multitude of gods, goddesses, numens and daimons, and thence an evolution started toward monotheism.

Everybody may believe in what he wants. We can start from the point we still have records. And it is hard to deny that Classical Romans had a multitude of deities with rituals, priests and such.

Since German Romanticism and Karl Marx we like to look at Greece and Rome as "Humanity's normal childhood", including their polytheism. That may be right. However when we confront happy old polytheism with sad Middle Age Christianity, I have my doubts. Anyway, until Constantine I the converts did convert against state authorities, and still they were converting. On the other hand, High Middle Ages were anything but sad in Italy, while we do not know too much about the happiness and fun of pagan Northern Germany.

But it is sure that Greek & Roman polytheism was similar to a natural forest compared to an artificial one of modern ages. In Greece religious persecution was almost impossible and everybody might emphasize that side of religion which he wanted.

Greek Pantheon was artificially organised around 12 chief deities, half male, half female. However this resulted only in moderate Law and Order. It was a minor matter that Chief God Zeus and Chief Goddess Hera always quarreled: theologians took the idea simply from marriages. But it was not known if a unique Law existed at all.

Zeus maintains Law and Order. Stealing is a sin, there are laws again theft. However Hermes is God of Thieves, a thief can ask him to help.

Zeus, Hera and Hestia maintain family, marriage and such. They are strictly against adultery (of humans). Aphrodite helps all lovers, including lawless ones. And so on.

Are strict laws (e.g. natural laws) in existence at all?

From this forest something starts to crystallize. Romans were more familiar with Law and Order that Greeks, and at the last centuries of the Empire they elevated 3 of the chief gods, Iuppiter (=Zeus), Iuno (=Hera) and Minerva (=Athena), the Capitolian Triad, to a higher status. E.g. in a lot of provincial cities they erected the statues of these 3 on the Forum. From this a tripolarity (n=2; see previous Part) might have evolved, but there was not enough time.

However there was in India. There from Vedic times Rishis tried to make some order among the innumerable devas and asuras. (Note that they had two sets of gods. That is not exceptional. The same was true in Iran, only there the ahuras were good and daevas bad. In Scandinavia there were the rather peaceful Vans and the more martial Aesir group, internationally known from Wagnerian operas.) Step by step the Trimurti crystallized: 3 chief gods as three forms #12 of a common godhead. Brahma, the Creator, Vishnu, the Preserver, and Shiva, the Destroyer.

So in present-day Hinduism a tripolar structure exists. See for analogy the previous Part; n=2 (more or less).

Ardeshir Mehta in his study about Prophet Zarathushtra (Mehta 2001) points out that Zarathushtra organised the same religious tradition as Vedic and post-Vedic Rishis, only into a different scheme. In some sense this was known for some time. The Only God, Ahura Mazda is the Great Ahura, which would be Great Asura in India, and sometimes there Varuna (=Uranus, the starry sky) was called the Great Asura; and there were speculations that Ahura Mazda's proper name is Varuna.

But Mehta lists a lot of more intimate identities too #13, and he emphasizes that Zarathushtra liked maximally simple structures. Indian philosophy saw 3 "colours", white, red and black, behind human nature, parallelly to the 3 "castes". Then Red (dynamic, as fire, &c.) corresponds to warrior caste, or energy. Instead Zarathushtra simplifies to White vs. Black. (See Part 6.)

And this is his fundamental religious idea. White vs. Black. Truth vs. Lie. Good vs. Evil. Duality. There is but one God; but below Him hosts of Good and Evil (surely ahuras and daevas) fight.

Old Iranians, Indians and some Mittannians called themselves (could you imagine, what?) "nobles", which is Airya in Avestan (Iran comes hence). So when German National-Socialists adopted Aryanism, they adopted also the Struggle of Light and Darkness. Philipp Lenard, Nobel Laureate in physics (originally from Pressburg, Hungary) adopted too the idea, and spoke about Aryan physics where Light and Darkness fight, refusing too complicated Asian ideas in physics. Zarathushtra might have agreed, except that he was Asian. Lenard was against Einstein and Relativity, he was feeling some complicated Lie behind because he did not understand it. But now it seems that Einstein was right: Space-Time does exist (n=4) #14. So Zarathushtra produced a simple scheme: it was too simple for physics, but may or may not be proper for religions.

I will not discuss the origin of Old Testament. Some people believe that Prophet Moses got the ideas of a new religion from God Himself, some believe that he invented it, some refer to evolution. However Evolution definitely works in religious ideas: people do not accept ideas too strange for them.

Again, there are some argumentations how pure was the monotheism in the first centuries after Moses. Now I do not have to discuss this. It seems that monotheism was complete in the time of King Josiah of Juda (end of 7th century BC), although Prophet Jeremiah briefly mentions a female godess, praised by women of Jerusalem. Ancient theology is adamant: God is One, infinitely above us. (There are angels, maybe a Zoroastrian idea.) One point in infinity does not have an internal structure, it is n=0.

Now, observe that God of Judaism and God of Christianity is the same; this is not a philosophical truth but a commonsense. Still in Christianity He has an internal structure.

Protestant theology uses a notion of "intertestamental period", a roughly 500 year one between the last writing of Protestant Old Testament (and Hebrew Bible), Malachy, and the New Testament, whose parts were surely written in AD 68, see hints for Emperor Nero. This period is not represented in Protestant Bibles.

However the "intertestamental period" is very brief in the Catholic Bible. Its Old Testament follows the Alexandria tradition (from its first part called Septuaginta, on Greek language) and it contains books well after Malachy. E.g. the book of Jesus ben Shirach is obviously from 2nd century BC. The Makkabees describe events about 160 BC. Now, the Book of Wisdom, or Sophia is thought to be written cca. in 50 BC. Is St. Joseph already in existence?

Now the book speaks about Wisdom of God, which emanates from Him (7.22). It is His Wisdom, but lives together with Him (8.3) (and the Lord loves Her) and can exist outside. (I am translating through the official Magyar Catholic text.) Catholic theology thinks that this is at least the prototype of Holy Ghost=Spirit, or a link in the chain leading there. Let us accept this.

Holy Trinity is tripolar. Then up to 50 BC only one point without internal structure existed, from that time at least in Alexandria 2, and with Christianity 3, Father, Holy Spirit and Son (in historical order). Maybe somebody would not like the term tripolar, telling that they are not opposites. Then he may call the structure triangular. In particle physics baryon D++ consists of 3 up quarks. They are not opposites, all have spins 1/2, charge +1/3; but for SU(3) one is Red, one is Green, one is Blue. (But note that the Persons were concurrents in the prophecies of Joachim de Fiore (Toynbee 1979; Seidler 1964).)

Observe that historically the Third Person was the second. Also note that Sophia is Wisdom, in Greek, and of female gender, as the Hebrew Ruach, Mandaean-Aramean Ruha and Greek psyche (all spirit). (This is the reason that above provocatively I used feminine gender for Wisdom. Note that Wisdom was also seen as a maiden by Muid ad-Din ibn al-Arabi, see e. g. Armstrong 1994.) It seems as if Sophia were the Septuaginta (=Catholic Old Testament) prototype of the Holy Spirit, and the Catholic Church seems to consider similarly.

Originally the 3 corners of the triangle were not regarded as equally strong. Roman Church determined at the Frejus Synod in 796 that not only Father can generate Holy Spirit but Son can as well. The Latin text speaks about the Holy Spirit generated "by also the Son", in Latin "Filioque", and so now Western religions, Catholic and Protestants together, are called filioque. Greek Orthodox Churches are still at the previous, asymmetric stage. Greek Catholic, or Unitus Churches recognized the filioque thesis when making the agreements with Rome, cca. 1700.

Pentecostians tell that they pay equal attentions for all 3 persons. Other Protestants, Catholics and Greek Orthodoxes seem to believe that pentecostians overemphasize the Holy Spirit. Each religion can be represented as a point in a regular triangle.

As we saw, the idea of Holy Spirit is slightly older than Christianity. So it is not surprising that sometimes Judaism also assumes some internal structure of godhead and even trinitary ideas appear as early (albeit in rudimentary stage) as at Philo of Alexandria (25 BC-50 AD) who observes the Mamre triple theophany (Gen. 18, 2; for his comments see his On Abraham XXIV-XXV). See also the comments of O’Connor (1984); corners of feminine Sophia and Masculine Logos still coincide. With the crystallization of a Christian Church this treand weakens in Judaism. Hovewer note Kabalist Abulfeda (Armstrong 1994) in 13^th century.. Internal structures are quite explicit in Kabala. But that structure would need much more discussion,

This internal space of godhead is not Riemannian; metric is not given to it.

Sounds of speech must be representable with some acoustic data as frequencies and amplitudes. It is sure that gesticulation, mimics &c. help understanding, but radio speech is understandable without them.

Some sounds of speech are not stationary. Central European [r], for example, has a slow periodic component. Diphtongs start with one characteristics and end with another. Obviously stationary sounds are easier to represent. At least for European languages the phonemes can roughly to be classified into 3 groups:

Nonstationary consonants (stops, affricates, &c.)

Stationary consonants (liquidae, sibilants, &c.)

Vowels.

It is a general belief that vowels are the simplest.

Of course, the border between vowels and consonants is not absolutely clear. In Slovakian, e.g., liquidae [r] and [l] are grammatically almost vowels. Length is denoted by a prime on the vowels (e.g. a-á), and the same trick is applied on r and l, only I cannot demonstrate this on HTML. A syllable is "a group of sounds with a vowel, or, in its lack, at least an r or l". Still, everybody believes that he knows what is a vowel. So let us remain at vowels. How much are they, and what is their relative structure?

Living languages, which we can directly investigate, are diverse. There are languages poor and rich in vowels. There is no living language without vowel or with only one vowel. Sometimes a Caucasian language (Abhazian) is reported with only two vowels, [a] and [u]. But it is sure that Classical Arab is a 3-vowel language with only [a], [u] and [i]. The upper limit is questionable, but Samoyed languages contain 10-11, Magyar 14 or 15 (according to dialects), and Chinese with musical tones probably even more.

Now, Indo-German languages form a close group, extremely well investigated and with records back to 4 millenia. Let us see the Indo-European vowels.

There is a general belief that the number of Indo-European vowels, at least until no strong external influences were present, is/was 5.

Indeed, Latin alphabet contains five:

a,e,o,i,u

Also, Greek has 5 short monophtongs

a,e,o,i,u

The two simple (?) long vowels h and w are considered as just long counterparts. In old Latin Greek borrowings got [u] in place of Greek u (e.g. satura). Old Indo-German reconstructions also like (a,e,o,i,u), see e.g. the classic Brugmann (1904).

Some linguists reconstructed a sixth Indo-European vowel, the Swa Indogermanicum. This would have been a short vowel, with indefinite quality, not unsimilar to the vowel in English [girl]. However it is difficult to guess the importance of an indefinite sound in reconstructions; the indefiniteness may be the deficiency of reconstruction as well.

However there are cases when a living, or dead but well documented, language shows up a vowel impossible to put among the Canonical Five. But let us see first the system.

There is little doubt about the relations amongst the 5 Latin vowels. I write simbolically:

Table 1: Structure of Indo-European vowels

The horizontal line is the high/low opposition: [a] is low, [e] and [o] are middle, [i] and [u] are high. Vertically we see the front/back one [i] and [e] are front, [u] and [o] are back, and [a] is maybe neutral. The front ones and [a] are unrounded, the back ones are rounded. The tentative Greek system is almost the same, only the back high one is unrounded. (However maybe there was no unique Classical Greek system: remember the Doric [a] in place of Ionic [e] as in damos/demos and in a lot of other pairs, and think about Aeolic peculiarities. We have predominantly Attic/Ionic manuscripts while Tzakonian, inheritor of the language of the winners of the Peloponnesian War (Brugmann 1904; Anon 1997) is just dying out.) The system is indeed meaningful.

Now, Gothic is very well documented. It had its own alphabet, starting from Greek letters. It has monographs denoting monophtongs, digraphs denoting diphtongs and also digraphs denoting monophtongs. Opinions are equivocal if IU was a diphtong, diphtongoid or monophtong (Moulton 1948). It would be simple to assume a diphtong behind, but note that two digraphs, AI and AU, thought diphtongs for a long time, now are regarded as monophtongs, quite logically the lower versions of E and O. Note also that IU would be the only digraph denoting Gothic diphtong (EI is also monophtong, a long high [i], and AW appears only in loanwords).

Now assume by analogy that IU also stood for a monophtong; what was its quality? Since both I and U are high, IU was probably high too. Greek u is used by Gothic in Greek loanwords (that is W here), so it is not probable that IU would have had an u -like quality. Then what? Of course, one always may look for a strange diphtong behind #16.

But in some Slavic languages there is too a sixth vowel, Y, the velar pair of palatal I. It seems as if proto-Slavic had two I-type sounds; and proto-Slavic was neighbour to Gothic in present Ukraine. In a lot of Slavic languages palatal/velar opposition is very important. In Russian Y/I dichotomy is usual in suffixes according to palatality/velarity of the stem, and the quality of the two sounds are quite different; while U is also present. In Ukrainian the situation is quite similar. In Polish y/i is also velar/palatal; other qualities much differ in Northern Poland while going to the Carpathians the difference is decreasing. In Slovakian, inside the Carpatians, now no quality difference is reported but it was reported as lately as 1919 from the Eastern end of the Slovakian linguistic area (Gerô, 1919). Otherwise, 4 consonants (t, d, l, n) are palatal before i, velar before y. Situation is almost the same in Bohemian. Today the qualities of i and y are the same, but long y (y’) is pronounced in the Middle Bohemian dialect as [ej]; but t, d and n are palatal/velar before i/y.

There is something also in Cymru (Welsh). An authentic source (Bowen & Rhys Jones 1960) tells that Welsh written U is an i-sound. In South Welsh it is an ordinary [i]. However in North Welsh "it resembles an ee pronounced as far back in the throat as possible". By other words, in North Welsh U stands for an unrounded, high, back vowel, while unrounded, high front Y is also present, as well as rounded high back W. This is also not the reconstructed Indo-German structure.

Present German has 3 additive Umlaut vowels ä, ö and ü. However this may be a late accession.

Gothic reconstructions of monophtongs use two sequences starting from the common, very low A. Then front vowels follow each other as more and more high (and all unrounded): AI (short, then long), E (maybe short, then long), I, EI (maybe short, then long). The back sequence, always rounded, is: AU (short, then long), O (maybe short, then long), U (short, then long), maybe IU. OK, long ones are higher via physiology; even then this is 5 grades including A, 9 vowels compared with the "canonical five".

And Mehta (2001) tells that Vedic texts sometimes contain a vowel written as "i" but it is rather "ü" (Rüshi). He must know better than I; I only tell that Gothic IU, Slavic Y, North Cymru U and Vedic Ü in Rüshi are too much for me to believe in 5 and just 5 original Indo-European vowels. I will return to Latin; but we can go toward the other extreme too. Laryngeal theory tells that proto-Indo-European contained 3 laryngeal consonants, symbolically denoted as h1, h2 and h3. Some of them remained consonants in Hittite and other Anatolian languages, and maybe in some cases in Armenian and Albanian. You can see examples for various reflexes in various languages in Mayhrhofer (1986). Otherwise they became vowels, enriching the vowel system (Lindeman 1981). Then why just 5?

A lot of non-Indo-European languages seem to have (according to alphabet) cca. 5 vowels. I would like to question this belief, on the example of Uralic and Altaic languages.

The literature of Uralic languages is not too old; the oldest authentic record is Magyar, some words in a Latin document from 1055 and a complete religious text from 1195. In addition, Magyar is official in Hungary only since 1841 (but in Transylvania from cca. 1550). However Magyar population was big and influential in Hungary and was not assimilated by Indo-Europeans. Similarly, Finns in Finland were always dominant for number.

The first Uralic Academy of Science was the Hungarian one which declared Magyar as her language. Magyar orthography was completely Latin-based, but used Bohemian and German tricks for distinguishing more than 5 vowels. The Academic orthography uses 14 vowels 7 short, 7 long. The existence of one more vowel (short, front, unrounded, mid-high) is obvious. One or two more vowels (back, high, unrounded) is highly uncertain. But even 15 is a lot. Finnish used German tricks, and so probably distinguishes all its vowels, 8 short, 8 long. Samoyed vowels are left for the next Chapter.

Altaic languages have old enough literacy. Turkish goes back to 720, and its alphabet then was adapted to the language. In Turkey (the Ottoman Empire) Arab writing was usual, but Mustafa Kemal, the Atatürk (Father of Turks) introduced a Latin alphabet in 1924. However, following Hungarian tricks.

Ottoman Turkish has a symmetric system of purely short vowels. Two of them (e and a) are front/back low unrounded vowels. Two others (ö and o) are front/back mid rounded ones. Finally there are 4 high vowels: i and ü unrounded/rounded front ones, i and u unrounded/rounded back ones. (Really i is written as i without the dot, but again it is not easy in HTML.)

However note that in Hungary and Finland national orthographies were formulated against Indo-European influence (I would tell with a Hungarian German expression: zum Trutz), and in Turkey without any Indo-European influences at all.

Neo-Latin linguists, from different afterlifes of Latin e's and o's in new languages conclude that "higher" and "lower" versions of e's and o's existed even in spoken Latin (indeed Osk wrote two more vowels). Then, indeed, the holy 5 of Indo-European vowels is impossible; still people seems convinced. Why?

Look again on Table 1, and then we turn to vowel recognition. According to Common Sense in speech acoustics, a vowel can be recognised from its first two, at most three, formants (higher ones simply characterizing individual timbres),which in turn means practically the frequencies of the local maxima in the Fourier spectrum. Now, the lowest frequency formant is most influenced by the low/high opposition, and the next one by the back/front one. Still, a rounded sound means lower second formant than an unrounded one. The explanation is in the structure of the speech channel. It is worthwhile to note that second formant differ less and less as the first frequency grows. (We shall see numbers.)

Now it is easy to see that with 3 vowels the anatomically maximal opposition is a triangle

Then [a] is low, and it is unimportant if it is front and back. The opposition is high, but there, at a lower first frequency, it is easy either to distinguish or to produce 2 vowels, a front and a back. Then an Indo-European anyways interprets the front one as [i] and the back one as [u], but, indeed, they are at maximal "distance" #15 if the front one is unrounded and the back one is rounded; and this is indeed [i] and [u].

Now 4 vowels would take a trapezoid, and this seems not to be used by Indo-Europeans. But the optimal arrangement of 5 (either for easy production or for easy recognition) is again a triangle, and that is Table 1. A low sound, which will be interpreted as [a] without the details; 2 mid ones and 2 high ones. Again, they differ maximally if the front ones, both the mid and the high, are unrounded, raising even more the second formant, and the back ones rounded, lowering it. And that is just (e,i) vs. (o,u). The "canonical Indo-European" structure may be rather a theoretical interpretation, an ideal; but, for any case, it is a 2-dimensional, tripolar or triangular system.

On the other hand, Ottoman Turkish is not a triangular structure. It is easiest to put the 8 vowels into a 3*4 grid, some positions empty (but we should not forget the physiologic convergence to the right, ignored in the Table):

Table 2: The Ottoman Turkish structure

Lotz (1975) gives definite two-formant data for Ottoman Turkish, although only averages, and it is not clear if male or female sounds. Anyways, his frequency data are:

Table 3: Turkish formant frequencies

Indeed, first formant frequencies are higher for low vowels, second formant frequencies are higher for front ones, and higher for unrounded vowels than for the rounded counterparts. Note the "vertical structure": vowels of the same first frequency can substitute each other in grammatical functions via Vowel Harmony. Since the idea is foreign for Indo-Europeans, Hamito-Semites and Basques, I give an example. There is a class of suffixes denoting the possessor. In Sg. 3 it is symbolically -I, meaning i, ü, i or u, according to vowels in the stem. So

ev=house, evi=his (her, its) house

göz=eye, gözü=his (her, its) eye

kiz=girl, kizi=his (her, its) girl (daughter)

kol=arm, kolu=his (her, its) arm.

The substitution is automatic, so indeed the suffix contains an abstract vowel, the indeterminate high one, with F1=250 Hz.

This structure, although not triangular, can still be formulated in two dimensions. However the Sölkup Samoied system is rather proper to be formulated in 3 dimensions. A Sölkup vowel can be:

1) low/high in three grades, 1/2/3;

2) palatal or velar, P/V;

3) labial or illabial, L/I

and the only combination which is doubtful in Sölkup is 1PL (Hajdú 1968).

My own first language, Magyar, is somewhere between Turkish and Sölkup for complicatedness. For Magyar we analysed measurements for formant frequencies in details (Borbély & Lukács 1989). The raw data came from many individual pronounciations. For i, ü, u, ö and o length practically does not influence the formants. For each vowel an elliptic tolerance region was calculated. The ellipses are roughly vertical, so it is enough to give ± values for the frequencies. (These are not errors. The averages have much smaller errors.) We handled male and female data separately; now look.

Vowel F1, male F1, female F2, male F2, female

i 263±34 265±26 2262±162 2517±177

ü 277±31 279±32 1812±142 2020±115

u 292±36 291±37 811±47 809±63

é 381±16 355±28 2162±169 2504±159

ö 398±33 412±34 1516±114 1702±108

o 410±29 432±40 908±123 897±107

e 529±41 631±63 1713±94 1928±127

a 554±41 577±30 986±71 995±95

á 757±82 883±63 1309±97 1489±125

Table 4: The Magyar formants: averages & tolerrances

Now what do we see? First, there is also a vertical structure (and the tolerance ellipses are approximately vertical too). Note that Magyar and Turkish are mutually unintelligible, and they do not form a Sprachbund either; Ottoman Turkish is spoken in Asia Minor, while Magyar in the Carpathian Basin. So here we do not see influences. Rather the structure must be common inheritance. Indeed, both languages contain the rule of Vowel Harmony, while the actual vowel systems differ. Obviously, then, the vertical structure cannot be expected in languages without Vowel Harmony, albeit physiology is able to force something roughly similar.

Second, observe again the genderless nature of Magyar. Male and female first formants almost coincide, and for any case, the tolerance regions mostly overlap. This is much less true for the second formants but they are not too far either. This is definitely not true for American English (Peterson & Barney 1952). So in Magyar, while male vs. female speech can of course be quite distinguishable, in first approximation vowel recognition does not have to start with distinguishing the sexes.

One might believe this feature unphysiological, so unnatural: smaller female body sizes automatically mean higher frequencies. However it is not so. Speech is almost exclusively taught by mothers, not fathers. So the child imitates maternal formants, and stops at the stage when the mother is satisfied. This means that in the Magyar linguistic community mothers expect less sex/gender characteristics in speech than in English: while these characteristics are not pushed completely to higher formants where individual timbres reside, the system itself is unisex.

Now, true, the space of vowels is not a Riemann space. It is rather a discrete grid. But this grid can be 0, 1, 2, 3 and more dimensional. 0 dimensional would be a language with a single vowel, and now such language does not exist. The simplest 1 dimensional grid has 2 positions, a single opposition. If Abhasian indeed has only two vowels, then its grid is 1 dimensional.

Languages with triangular vowel structure seem 2-dimensional, and then both Classical Arab (3 vowels) and Classical Latin (theoretically 5) are such. Gothic and Slavic languages would be best to be classified by a Slav; and what about Welsh?

Turkish dimensionality can be 2 or 3. But Nenec and Sölkup seem to be genuine 3-dimensional even if frequency analyses are out of reach for me. And what about Chinese vowels?

Some 10 years ago I planned to write a book or booklet in a similar topics with Dr. N. L. Balazs, New York State University at Stony Brook. Finally we did not have the time; however I learnt a lot from him, for which I am grateful. I acknowledge discussions about the topic of Chapter 5 with Dr. L. Diósi.

Can I disprove circus tricks? Can I disprove Philippine healers? No. Maybe Mr. Randy can. It is not my business. I think there is a trick. Circus acrobats and jugglers are not offended then.

But I can put it another, more unorthodox, way too. Physics works with reproducible processes. This means, amongst others, that with processes everybody can produce, maybe after learning, but then the lore is accessible. So Physics is everybody's tool to travel faster than sound, to see into ten thousand kilometers, to heat water and so. Indeed jet planes (based on hydrodynamics), televisions (based on optics, electron physics and colour theory) and stoves (based on thermodynamics) work every time for everybody.

Now some people tell that they can do things which others cannot do at all. Beware; people very frequently tell that they are supermen. In most cases this is empty boasting and that does not belong to me. In a few cases the subject indeed can do something which was believed impossible.

Then, again, in principle there are two possibilities. The first is that later Science clarifies how that was done, and then everybody can do it. An example is gambling. Originally even dices were expensive and common soldiers used knucklebones and such. Even when dices became general, they were not identical. Sequences were irreducible, so people assumed that somebody has the favour of Lady Luck, others not. Then step by step some reasons mimicking Lady Luck were discovered. E.g. a sheet of lead just inside the side 6 plus a skilled hand raises the probability of result 6 (and mechanics knows why). Then community declared that such dices are unfair. Still there remained too successful players. Then came Blaise Pascal focussing on the mathematics of chance, and found that some bets and games had not given equal chances and by the new discipline most actions of Lady Luck vanished. Now everybody could learn how to throw a lot of 6's with a prepared dice.

Now comes the alternative possibility. Some people claim that they still have the favours of Lady Luck, e.g. they can throw more than 16.67 % 6's even with others' dice. Physics would think first about temperatures or such; if results were very convincing (they are not) then even telekinesis would be investigated, and so on. Telekinesis is not impossible; it is highly improbable and no viable mechanism was suggested at all. If physicists were to detect it, then they would try to do it, and if successful, everybody could do later. But assume that they are unsuccessful, and some people tell us: look, we have the favours of Lady Luck, and She is giving us more 6's. She is a higher Force, partially controlling Reality. There is no way for you to be friendly with Her. You will throw always 16.67 % 6's. And assume that this is true! (If not, it is boasting and does not belong here.)

If so, then there are 2 kinds of people. One is not influenced by Lady Luck, the other, the minority, is. Then I, as a physicist, would suggest simply to the "normal" majority: do not gamble with the luckies! Maybe State would list the luckies and gambling with normals would be a felony. It seems that witchcraft hystery and trials started with people boasting that they can milk the neighbour's cow in an action-at-distance; or they can direct somebody else's sexuality.

The boasting was so successful that societies became afraid and reacted violently. Then either all witches died out in the bloodshed (with a lot of normals) or, and I think this happened, there were only normals even at beginning. However I do not want to force my opinion on anybody.

And now: what if Chosen People can travel to dimensions whither the majority cannot? To my best knowledge I am not Chosen. I doubt if somebody is such; but that is my opinion, not obligatory. Then my task is to find out what can we do. Our space is of 3 dimensional. Physics is our lore, instead of magic which we cannot use. Only I believe that nobody can.

Since the book of Trbuhovic'-Gjuric' (1969) or rather since the German translation, many scholars (definitely not physicists, however) ask if it were not proper to call Special Relativity "Einstein & Einstein Theory". I completely agree with the anonymous author (Anon 1999) who writes: "It is unlikely that Meliva's [!] contributions to Albert's published works will ever be determined precisely.". I am surprised, however, about the first sentence "The discovery of the letters between Mileva and Albert has caused some to speculate on the amount of involvement Mileva had in Albert's work.". I did read the letters, I am relativist and a Hungarian citizen as Marity Mileva, still I am unable to find any hint about Marity’s role in Relativity in them. No surprise; the first Einstein paper about relativity was published in 1905. In the Love Letters Volume the last Marity letter is from Budapest, Aug. 27, 1903 (I bet from Keleti Station, changing trains going to her parents very probably on the Budapest-Kelebia-Szabadka-Ujvidék line); Mrs. Einstein is either in the first month of pregnancy and the placenta is not yet developed (Bérczi, Holba, Lukács & Papp 1996) or is in her usual depression; she writes: "I'm not feeling well at all.", and asks Albert what is he doing (meaning profession). Albert's answer is the last Love Letter, telling he does well as patent officer, his boss is satisfied. The first half of the letter is private life, and has a reference to Lieserl, the mystic "Einstein's Daughter". She had been given away; and look: the child-to-be is Hans-Albert, later teaching hydrodynamics at Princeton, then Berkeley. Since Hans Albert was 10 year old when the Einsteins divorced, we can tell that Marity made physicist from Hans Albert. So Lieserl may be called Marity's Daughter as well; anyway we do not know anything about Lieserl's intellect at all.

To be sure, there are hints about Electrodynamics of Moving Bodies; but only in letters written by Albert. In Letter 8, Aug. 10, 1899, Einstein explains that the electromagnetism of moving bodies should be reformulated, ether should not be introduced but laws should directly be applied on vacuum. The answering Marity letter is posted at Káty, Bács-Bodrog County (Hungary), and she does not react at all to the electrodynamics of moving bodies, but tells that she sheldom goes even into the garden. In the next letter Einstein tells that "I had a good idea..." about relative motion to luminoferous ether... but then "But enough of this! Your poor little head is already crammed full of other people's hobby horses...". In Letter 11 Einstein writes about his paper about relative motion of the luminoferous ether. I guess this "paper" was a university elaborate, never published anyway, but it was his paper, not "ours". I stop here. To be sure, I think that later, verbally, they discussed the electrodynamics of moving bodies. But it seems it did not interest Marity too much (mildly put). For a physicist it is clear when another physicist is uninterested but polite.

Still Trbuhovic'-Gjuric' refers A. Ioffe who writes somewhere that on the manuscript of the great relativity paper (Einstein 1905) the authors were "Einstein - Maric'". I already told why I do not believe in "c'", but nevermind. This would mean that either A. Einstein or M. Planck (the chief editor of Annalen) committed an unforgivable sin against copyright. Without serious evidences this is simply slander.

However I can imagine that there was an earlier Einstein-Marity manuscript. Marity's diplome work was thermodynamics. Now look. In Letter 23, from Milan, Oct. 3, 1900 Einstein writes Marity: "The results on capillarity I recently obtained ... seems to be entirely new ... If this yields a law of nature, we'll send the results to Wiedemann's Annalen". We. There is an Einstein paper about capillarity in Annalen from 1901, but only Einstein.

Well, nobody knows how much was Marity's part in capillarity. But in another Milan letter, from March 23, 1901 there are 2 paragraphs about the Dulong-Petit Law, ending with "See if you can find some literature on this!". (Then chirp-chirp.) In the next letter again two thermodynamic paragraphs. Milan letter April 15 (Letter 28) is decisive. About molecular forces in gases Einstein writes: "...to apply our theory..." and again "...our constants c...". Then a long paragraph about physics. For me it is clear that they together had a formalism of their own, about heat transfer or such a problem of thin gases.

In the next letter there is again a vague note about energy of light; plus an invitation to travel together from Como to Zurich. And we do know that there was an answer, not extant. It seems, Einstein never got it, see the next 2 letters. But next day Mileva sends another letter telling that she thought yesterday that she would go but no, she would not because "...it seems I can have nothing without being punished...". Nothing about energy of light. I can guess that i) her menstruation did not appear (by calendar it is Lieserl!); or ii) she had bad news from home; or) iii) she had bad news about Einstein's behaviour; or iv) she was in depression. Most probably iii) or iv), since on the next day she again accepts the invitation and starts to organise the travel. But no mention of energy of light at all.

I stop here. There are Einstein articles in thermodynamics in 1902. There is no Einstein-Marity paper although "...to apply our theory...". But: Mileva is pregnant, and Albert's carreer is important for the future of 3 persons.

I think Marity agreed that Einstein publish the paper alone (although it would be difficult to prove it). I also think it was naughty to say decades later that the diplome work of his first wife had been boring. The letters tell otherwise. Einstein lied at least once; not as a man to a woman, but as a physicist to a physicist about physics. I wonder why he was so angry after 30 years.

Marcel Grossmann was born in Budapest, Hungary in 1878. Quite recently Hungarian historians became interested and clarified his origin. His father was Swiss, Jules Grossmann, who cca. in 1870 started business in Budapest, and remained there until 1893 (Fehér & Hajdú s.a.). In 1882, he, with a partner written alternatively as Rauschenbach and Rausenbach (Névmutató s.a.), founded a factory of agrarian machines which was successful. In an official catalog he is written as Grossmann Gyula (Névmutató, s.a.) indicating that he was handled as a Magyar. (Or, for any case, as a Hungarian.) So Marcel Grossmann lived in Budapest until age 15. Some knowledge of Magyar (better than Mileva’s) is probable.

Grossmann is younger by 3 years than Marity but older by 1 than Einstein. The 3 students are friends, the Love Letters amply mention him. In Letter 48 (Marity is at home in Hungary, Lieserl is expected within days) Einstein writes that "Grossmann is doing his dissertation on a subject which is related to fiddling and non-Euclidean geometry. I don't know exactly what is it." (emphasis is mine). Let us believe him; he did not know.

There is an Einstein lecture from the 30's, which I am translating to English from Magyar; the original is (Einstein 1933). It starts as "I am happy to tell several words about the history of my own research.". If somebody finds the original, it will be interesting to see how much changes appear in a translation through a language not Indo-German. However physics is language-independent. He tells about the equality of gravitating and inertial masses that: "I had no doubt about its validity even not having known the nice experimental result of Eötvös, which experiments became known me only later -if I remember correctly". A complicated and uncertain statement, so I try to formulate it otherwise. Einstein tells that Eötvös measured the equality with great precisity. That is right; Eötvös proved the equality to 6 digits about 1900 with a torsion pendulum (on the ice of Lake Balaton, to be sure), and to 8 digits about 1908. This latter work was sent to a competition at a German university, won the gold medal and became published in Annalen der Physik as late as 1922; however the result was known. Einstein seems to remember that he did not know the Eötvös experiments in 1912 (when starting General Relativity with Grossmann), still he did not doubt about the equality. He might be convinced, since Bessel proved equality to 4 digits in 1841 with astronomical methods. He knew the experiment only later (maybe in 1922 when it appeared in Annalen); if he remembers well.

He does not remember, for any case, consequently. In 1946 (Einstein A. 1949) where I do not have year but it starts as "I sit here, 67 year old...", he writes that when he started to include gravitation into relativity (so cca. from 1908), he knew that the new theory should fulfil some principles, e.g. "It was known from measurements of large precisity (especially from experiments with the Eötvös pendulum) empirically that the gravitating and inertial masses of bodies are equal."

Now look. My aim is not to prove Eötvös's role in General Relativity. Einstein could have concluded in the equality from Bessel's results (if two things are equal to 0.01 %, maybe they are equal for any). I am interested in the way of scientific research in the Einstein-Marity-Grossmann triangle and want to reconstruct what happened. And I am relativist as Einstein and Hungarian as Marity.

Now, although Einstein & Grossmann 1913 has priority, (Einstein 1916) is the classical paper; there General Relativity is ready in its present form. At the middle of the paper Einstein notes that gravity causes the same acceleration on any body, which is another, equivalent, formulation of the equality of gravitating and inertial masses. Then there is a footnote: "Eötvös has proven experimentally that this is true in gravity field with great precision". No explicite citation of a paper, however. So he remembers incorrectly in the 30's, and maybe correctly in 1946; but anyway there is a constant hazyness. My idea is that the uncertainty is the consequence of his private life; now I continue in historical order.

Trbuhovic'-Gjuric' (1969) writes that the Einstein-Einstein marriage became disturbed in Prague (in 1911-12); they could quarrel on things quite trivial earlier, and in mathematical problems Albert asked the help of somebody other instead of Mileva.

Now, this disturbing Third was Grossmann. And if Trbuhovic'-Gjuric' thinks that Mileva could offer the same, she is very much in mistake. Einstein needed Riemann on non-Euclidean geometry (although he did not know it originally), Grossmann knew the theory (as we saw it in Love Letter 48) and we do not have any evidence that Marity would have known it. Now Riemann geometry is known by some, say, 1 % of physicists (I know it, of course); 90 years earlier such a person was a white raven. Mileva Marity may have been a nice individual (I do not know her psychology except the depressions), she was the mother of Einstein's 3 children (of which they gave away the first, to be sure), but she was unable to do Riemann geometry. What to do?

Next year Einstein and Grossmann have constructed General Relativity (still without field equation); Mileva is angry (either because of this, or for something else, or both; I do not know) and will not follow Einstein to Berlin. It is divorce practically; de iure in 1919. Einstein remembers in 1946 that he knew about the Eötvös experiment in 1912; surely he knew about 1916. We know that the Einstein-Eötvös correspondence started in January 1918; but also there is an Einstein letter to Wien in 1912 (Illy 1989) in which Einstein explains the torsion pendulum, the central idea of the Eötvös measurements, not used by anybody else, to Wien. Vizgin (1981) tells that a problem of Langevin might have been solved in this way. It seems as if Einstein got informations about Eötvös around 1910, but he could not make it more definite in 1916 and later he became even more hazy.

My opinion is that all evidences suggest Marity as the source. I am not proving anything but tell a psychologically possible story. But first I tell that Eötvös was a Baron, and Hungarian minister of education & religion in 1894-95. He was an aristocrat and a physicist. He did not have to work and publish. That was done for passion and fame. Therefore he mainly published his results in the Yearbooks of the Hungarian Academy of Sciences; nice books bound into leather with golden inscriptions and such. This explains why his great 1908 measurements were not published until his death. They were simply more correct even than the previous ones and he already had the large gold medal and the fame; why to write down once more? So much about Eötvös and his publicational habits.

Now imagine the Einsteins in Prague. Marriage is deteriorating; no surprise, the wife is bored. They are far from home, no friends. Prague in itself would not be more boring that a Swiss city (no less either), but no friends. A person inclined to depression is not too strong to find new friends. And she is physicist. Henceforth it is reconstruction, or novelette. The wife is bored, goes to the university (the German university of Prague was small enough, and, as I remember the building, not too decorative) and would like to chat with Albert. However Albert is just lecturing. Would Madam visit the garden first? No! I go to the library. (She is a physicist. That is an indelible character as being a Catholic priest.) Then she can learn something; but what? She did not make any independent research sine 1898.

Maybe she wants to help Albert about relativistic gravity. Maybe she does not want either that, but to read anything. There are the nice volumes of the Yearbooks of the Hungarian Academy of Sciences, in leather. She is Hungarian. (Yes. She is a Hungarian citizen of Serb ethnicity. We are before First World War.) Let us look into. What is happening in the Old Country?

And then there is no way not to found Baron Eötvös. The Baron measures each year and appears in the Yearbook. To be sure, the Einsteins knew his name for at least 10 years: Eötvös made fundamental work in capillarity and the first true Einstein article was in capillarity. Good solid works, these, on the equality of gravitating and inertial masses. Albert would be interested.

Now, I do not know if she wants to help or wants to raise prestige. Maybe both. If the first: I read it and tell Albert. If the second: I tell Albert lest he believe that he knows everything and I nothing. The result is the same. I tell the second variant.

• Darling, any development with gravity?

• Yes, honey, I was thinking about. I really believe that theories without equality of gravitating and inertial masses are impossible. You know; Bessel has shown the equality to 4 digits.

• Eh, Albert! You and your Bessel! (To the East of Ujvidék (Novi Sad) and Titel there is a German group of people called Schwaben; they are our Germans. Albert is also a Schwab. There are the Schwaben; and there are we. Myself and Baron Eötvös. He is not a Schwab either...) He verified the equality years ago to 6 digits and now he is near to 8! That is something, is it not?

• And honey, how he can do this?

• How, how. Of course by a torsion pendulum. Cute compact apparatus, isn’t it?

• Honey, I never heard about!

• You know, there is first a wolfram wire...

Curtain falls.

Then in 1912 Einstein is very convinced about equality. He tells it Grossmann and they work. In 1916 he writes the Annalen article; but he does not know the reference. He could write to Mileva but they are not in good terms. OK, he writes a footnote.

And 17 years later either he does not want to remember to Mileva or he is so hazy about the torsion pendulum that he genuinely does not remember.

Trbuhovic'-Gjuric' suggests that the later work (the Unified Field Theory) was unsuccessful, because there was no more Mileva. I do not know. Mileva was surely more inspiring than the second wife Elsa, who was very cultured (which Mileva was not; read Love Letter 1: "...our little land of outlaws..." meaning the neighbourhood of Titel), but was neither a physicist nor exciting (anyway, she was second niece to Einstein). Still now I, and the physicist consensus, think that even Einstein, Marity and Grossmann together could not have solved the problem in mere 4 dimension.

If we want to see the influence of higher dimensions, the simplest possibility is to repeat Eötvös-type measurements with modern technique.

I do not know if the space of dumb-bells, which is 5-dimensional, is true or not, because I do not see what is "true". The dumb-bell can be described as one point in a 5-dimensional space or as 2 points + a constraint in 3; the two descriptions are equivalent. However in Quantum Mechanics two electrons must be described in a 6-dimensional one; the 3-dimensional is only approximation. It is another matter that Quantum Mechanics is also an approximation. Everything is proven sooner or later to be an approximation.

Here I tell only one nicety. A gas of one component has a 2-dimensional state space. An ideal gas has a state space of Euclidean geometry; nice. Now the space of a van der Waals gas without attracting interaction (so with only the volume exclusion) is of constant curvature (you can find the necessary formulae in (Diósi, Lukács & Rácz 1989)), and the constant curvature is negative. So the state space of the simplest van der Waals gas is of Bólyai-Lobatschevsky geometry.

Colorimetry started on men. In the 19^th century only male university students were available; afterwards mass testing continued with railwaymen, later soldiers, then car drivers, originally all men. Results were simple. Some 90 % is normal trichromats, some 10 % dichromats or anomalous trichromats. Overwhelming majority of the problems appear in the red-green subsystem (protanopes/protanomals and deuteranopes/deuteranomals); tritanopes are very rare.

Sporadic observations on females gave much smaller rates for anomalies. Obvious explanation: some genes of colour vision are on the sex chromosome X. In females X's are paired as the autosomes, so an error very probably is corrected by the other. In males even recessive mutations are manifested. Indeed now the opinion is that red and green pigment genes are located on Chromosome X, while those of blue on Chromosome 7.

But for a long time experiences suggested that the situation is not so simple. Wasserman (Wasserman 1978) tells some unexpected experiences. For example, the above reasoning would predict M²/F~1, where M and F are the colour anomaly ratios in males and females. But the ratio geographically varies from 1.30 in Northern Europe to 0.17 for Amerind, Eskimoes and others.

With the advent of massive female presence at universities cheap comparison of colour vision of sexes became possible; and then it turned out that 1) female colour abnormalities are more frequent as believed earlier, but 2) anomalous females tend to avoid the tests. Because the influences of psychology a female psychologist invented a new type of test and then she described cases when female observers were observed as observing the test to learn correct answers beforehand.

Wasserman's opinion is that women are embarrassed if their colour vision is abnormal, while men want to know if it is or not. And indeed, roommates of colour-abnormal female students reported that the subject showed unusual choice of clothing (obviously about matching colours).

Now, in some sense this explanation is satisfactory. Obviously perfect clothing is much more important for a woman than for a man. However this does not explain why 1) female students tend to avoid the test and if cannot then 2) try to learn the answers of others. In clothing skills &c. woman's concurrent is another woman, not man. And if a female student is colour blind, the main harm is caused by the colour blindness (wearing unmatching colours &c.) not by being it known.

However now another psychologic aspect is possible. While overwhelming majority of men are homogeneous for colour vision & discrimination (90 % normal trichromat, with the same error ellipses &c.), there is a continuum among women. Some may be tetrachromats, some trichromats but with a double-peaked pigment (some in red some in green), some normal trichromats. But the mothers of some of the tetrachromats are again trichromats, and then whence can the girl learn the fourth dimension?

So the niceties above normal trichromacy are similar to a secret lore, e.g. witchcraft, learnt from wiser women. And then it was natural that female students observed each other's answers and copied them.

And you see: there may be superwomen able to (not to move, but see) in a dimension where others cannot.

Different regions of World define the object behind the English word "nation" differently. In Western Europe and USA it is now generally understood as a synonyme for "citizenship". However, e.g. in Spain somebody may have a Spanish passport and still can be Spanish or Catalan or Basque, at least. In Britain, one can be e.g. Scot or English; in Scotland the State Church is Calvinist, in England the Church of England. In the Third World societies are less homogeneous: e.g. on Fiji Islands ethnic Fijies and Hindu settlers are generally vote solely for their own fellows and would be surprised if you discussed the Fiji Nation. Or in Afghanistan there is no Afghani Nation, but there are different tribes and tribal alliances. Up to now this was considered something which will be grown over in time; however in European Union there is no European Nation but English, French, Dutch &c.

Now, Eastern Central Europe and South Africa seem something in between USA and Afghanistan. South Africa develops a multiracial, rainbow culture and society. But there are visible (albeit not well-defined) groups or condensation nuclei inside. I am not trying to predict future, and of course do not know enough; but I do know the problems with notions. And obviously, if solidarity within groups is very strong then electors vote according to group solidarity and then the dimensionality is number of strongly bound groups minus one. Now I switch to Eastern Central Europe, which I know well enough.

The Carpathian Basin was occupied by Magyar tribes in 896 AD. In that time the Basin was a mosaic. In the northern mountains Slavs lived, ancestors of modern Slovaks and at the far east those of Rusyns. The hilly region West of Danube was populated by Franks, Bavarians, small Avar groups, indefinite Slavs and some Croats. The plains East of Danube housed Avars, Bulgar Turks, Bulgar Slavs and Gepids. Transylvania was populated by us (Magyars doubt this and I will not go into details what "us" means here) and some more Gepids. Some other ethnic groups may claim also old presence but they are in mistake.

Then Magyars came in, and after 104 years the Regnum Hungariae, the Kingdom of Hungary was organised. Now comes Richard Marsina, Slovakian historiographer, high officer of patriotic organisation Matica Slovenská, cca. The Slovakian Mother, writing about the Slovakian ethnogenesis (Marsina 1997). The title is "Ethnogenesis of Slovaks". Ethnogenesis; since the Slovakian ethnos was not ready then; he tells that the ethnogenesis started cca. in 828, with consecration of the Nitra church and completed in the twelfth century, within the Hungarian State.

Now, English "nation" comes from Latin "natio". The Natio Hungarica was originally the nobility and priests of Hungaria/Hungary, and it is a supraethnical notion. We (I mean, Dr. Marsina, I, and a lot of other Eastern Central Europeans) do know it. He, in the English text, writes: "The descendants of the Nitra Sloviens and the Slavs living to the east of them lived, hovewer, in the same state after the fall of Great Moravia, in the Kingdom of Hungary, with the hegemonic Magyars. For the Magyars, the Slavonic population living all over the northern part of the Kingdom of Hungary were united (equal) Slavs..." (Hence you can see the difference between Magyar and Hungarian.) He tells that Slovakian ethnogenesis was possible and even not slower than at self-governing Slavic territories because the Magyars handled all the Northern Slavs the same way. Therefore they (i.e. Magyars) did not hinder the ethnogenesis. I repeat, the Matica is the most patriotic Slovakian organisation, not Magyarophile at all. He tells also that in Middle Ages "Outside of the Kingdom of Hungary a Slav from northern Hungary probably labelled himself (but was labelled also by others) as a Hungarus according to the country he came from.".

So both a Slovak and a Magyar belonged to the Hungarica natio/Hungarian nation, and in the same time one was Slovak, the other Magyar by ethnos. Maybe Afrikaans "volk" is ethnos, I do not know. But it seems that Afrikaans ethnogenesis is going on. Thirty years ago a Brown Afrikaner would have been a strange notion; now it is not, and Mayor Peter Marais succintly formulates that the frightened people in the laager are "Pale White". Not only white, but pale white.

Now one cannot predict the final result. Afrikaans ethnogenesis is going on. Patrick Cull already on Oct. 15, 2001 observed (Cull 2001) that DP is considered as a white party and NNP not. (Maybe Marais would tell that NNP is not pale white?) And Sekola Skello on Nov. 16 observes that DP is English with some Afrikaans-speaking members, while NNP is (colour-blind?) Afrikaner (Skello 2001). But the final size of a multicoloured Afrikaner ethnos (volk? Skello uses this Afrikaans word in English text. Nation?) depends on the organising idea.

Is it really the Afrikaans language? There are Afrikaans-speaking groups calling themselves other ethnos. The most trivial example is the Griqua nation. I would cite old Councillor Visagie, from the Council of Kapteyn Waterboer, telling: "'n Griqua is nie 'n swart man, en hy is nie 'n coloured", that is a Griqua is not black, nor coloured [instead of the English expression in the original text I would have expected kleurling or such, B.L.] (Matshikiza 1999). He may have appended: ...en nie ‘n blank. A Griqua is Griqua. So far it is true for Magyars too. But Magyars have the unique Magyar language while Griquas speak the same language as Afrikaners, Pale White, Dusky White or Brown. There seems to be a strong correlation now for being Afrikaner and voting for NNP. But Afrikaners are a minority in South Africa, and serious parties want to be majorities.

Now I close with sentences understood in Central Europe but maybe only here. I am sitting in Budapest (this in itself is not trivial; our tribe lives 1000 km to the East) when typing this, 1106 years after the Conquest which led to the State of Hungary and in which my tribe did not participate but made an alliance with the newcomers. (As the Croats, slightly later.) In the next 1100 years the Eastern Magyars, surely from East of River Don, but probably from Asia, so much mixed with locals that they are quite pale white, epicanthic fold and Mongoliasn spot rarities. Western anthropologists tell that they do not see difference from neighbours; we see still, but not too much. (My tribe is more Asian, Mongol spot occurs in some 10 %.) But the pale white people with straight legs and round eyes celebrated just now the millenium of the State and 6 years ago the millecentennary of the Conquest, whose leaders would have been surprised about the appearance of the people honouring them. Who will be considered the Founding Fathers of the Cape after 600 more years?

The Yezidi religion of Kurdistan originates from the Iranian religion, but became strongly influenced by the Muslim ideas (Glasenapp 1972). Now, in the original Zarathushtran religion Ahura Mazda is a single God. However He has internal structure via some "aspects" or "forces" of Him (Mehta 2001). Also, the forces of Good are fighting the forces of Evil, which are led by Angra Mainyu. This leads to a tendency to postulate two Poles, and dualism is a well-known Iranian tendency.

Now, we saw an example for isopolar religion in the Alexandrian Jewish community, writing the Book of Wisdom. (I take the term "isopolar" from Bérczi, Holba & Lukács (1994), where it stands for the symmetric growth of Isoëtes, Stylites and extinct Palaeozoic tree-sized lycopods compared to the opposite polarities of root vs. shoot in flowery plants.) God vs. His Spirit, or even God vs. Sophia did not mean opposites.) True; it developed soon into tripolar/triangular (Christianity). Maybe the most famous representative of the isopolar stage was St. John the Baptist who baptized by water and Spirit.

Now, a community exists, whose last prophet is St. John the Baptist: the Mandaeans in Southern Iraq. Their religion is dualistic and gnostic (Glasenapp 1972; Amara s.a.). Obviously bipolar Iranian influences helped the rudimentary isopolar tendencies of Alexandria.

Now, the Iranian trend led to opposites on a line (n=1), as we saw. Yezidis are nothing new for dimensionality. Still, they are new in something else. From time to time reports tell that they praise the Evil Pole. Obviously if there are two enemy forces, it is possible to go to the negative side; but 1) we know from politics (Part 7) that everybody has the tendency to call his side the positive; and 2) even in Iran it is general belief that at the very end Ahura Mazda = Ormuzd will win. So: why to join with the Evil side?

I admit first that it is difficult to reach the true teaching of Yezidis, because there is a big chatter about so piquant topics. Still, it seems that a special morality is behind, and this deserves an Appendix. Namely, the Evil is analogous (maybe homologous) with Lucifer of the Christianity: a kind of Archangel, who was the First Archangel; "only" revolted (Anon s.a.; Dadrawala s.a.). Now, at the end of times he will be defeated; but this is not enough reason to betray him. (It is not clear for me, if forefathers of the Yezidi joined him before or after the revolt.) At the end of time, after his defeat God will pardon him, the ex-Evil, and he will stand for his faithful people.

There is some dark heroism in this philosophy.

There is some argumentation about Neanderthal language. Note that we do not know anything of it. Reconstruction exists for the vocal channel of the La-Chapelle-aux-Saints Old Man (Lieberman & Crelin 1984), but now it seems possible that the original anthropologic reconstruction was erroneous which error then propagated to the acoustic one. However this is a complicated question; I am not taking sides and give here a reference to a site of my own (of course) where the reader can find ample references to speech ability of Neanderthals (Lukács 2001). It seems that their high vowels had the first formants of our mid ones; if they had vowels at all.

Now consider neolithic Homo sapiens. No problem with anatomy. Still, there is a theory where as recently as 4000 BC language was not spoken, but operated with mimics, gestures &c (Ginneken 1939). Just afterwards vowels were still absent and their role was first played by click sounds (existing now in Khoi-San languages of Southern Africa and also in Bantu Xhosa (e.g. the sound written as X). Later Jóhanesson (1967) suggested that ancestor of Indo-European and Semito-Hamitic directly evolved from gestures.

These theories seem absurd. However note that 1) we do not know anything about the acoustic structure of ancestor(s) of proto-Indo-European and Semito-Hamitic. And 2) Semitic languages are vowel-poor even now, with a secondary role of vowels anyways. As for proto-Indo-European now we know that a lot of vowels developed from laryngeals (Lindeman 1981), and then everybody may believe as he wants.

A language without vowels is, however, impractical. Vowels can be heard farther than consonants, pure consonantal speech is too low. Maybe clicks help, maybe a language "without vowels" is really without vowels, i.e. with a single arbitrary vowel which could be pronounced every place where it was needed.

We do not know and we cannot directly check. However Uralic linguistics is quite developed. Unfortunately the Uralic vowel system, so before 4000 BC, is not yet unequivocally reconstructed (however see reconstructed words at Harms (1974). The proto-Finno-Ugric system is reconstructed; unfortunately in 2 variants (Steinitz W. 1944; Itkonen E. 1946), but they are not too different. Both reconstructions contain 11 vowels, albeit the system differs from the present 3 dimensional grids of Sölkup and Nenec. Still, Collinder (1965). reconstructed some words and found 14 common stems between PU and PIE. I am not interested in the details; my point is only that the PU and PIE vowels are similar in them. So in some cases present U and IE vowels have common predecessors. So it seems that some definite vowels did exist in proto-Indo-European about 4000 BC. But now it is enough of this.

#1 I belong to the Uralic or Uralo-Altaic language family. So I take the freedom not to bother myself with the English problem of he/she and his/her. In my language there is no gender and still we survive; we have only one 3^rd person singular pronoun. If English-speaking colleagues (of any gender) regard the explicite genders problematic, they can eliminate the multiplicity of unnecessary linguistic forms; they are not really important, we succeed without them. So for me the "general subject" is "he", and it is natural for everybody speaking my language. And think about German: the "general subject" "somebody" is "man", which comes of course from Mann and not from Frau; and "girl" is "Mädchen", but she is an "it", because a Mädchen is little, ending with a "-chen", and everything ending with -chen must be of neutral gender.

In some Slavic languages adjectives can differ for gender even in plural. Then even people with genders can ask what form is proper for a group containing both men and women. The solution is simple: the group is masculine if it has at least one masculine member. Logical, is it not? I would like to avoid all these Nostratic niceties, unimportant for a physicist.

#2 Aristotle's Works were published by Andronicus of Rhodes, the head of the Peripatetic School c. 60 BC. That is the Canon, and when I cite a book of Aristotle, I am not too interested how the book was rewritten between 322 and 60. By the way, experts consider De Caelo really "genuine", meaning that maybe a student or a young teacher stenographed the lecture of the boss.

#3 A small minority cannot well discriminate his right from left. Similarly 10 % of men and 1 % of women are daltonians, losing a dimension of colour space; they are not representative. Let us proceed.

#4 The name of the lady is often written as Maric' (really the prime ' should be on the "c", but it is rather hopeless in an HTML); however this is anachronism and misinterpretation. The gravestone of the lady in Zurich is inscribed "Mileva Einstein, geb. Marity"; for the photograph see Gogola (1988). Here the "ty" digraph means some palatal affricate, existing in Russian, some Central European Slavic languages and in Magyar. It is produced if you make a very palatal "t", but it is no more a stop. Now different Slavic languages of Latin letters write this sound differently. Polish writes "ci", Slovakian "t'" and Croatian, indeed, "c'". The "ty" on the gravestone is Magyar.

However Mileva Marity, later Einstein, was not a Croat, but a Serb, born as a Hungarian subject (true, spent some years in a Croatian middle school when the father worked in Croatia). Both Hungary and Croatia use Latin letters, so in both states the Serbian name was transcribed from Cyrillic to Latin in official documents, but differently.

Now, Mileva M. was originally a Hungarian Serb, not a Croatian one. So she learned in school where the youngsters learnt Magyar as a foreign language that with Latin letters her name would be Marity. This "ty" is on the Swiss gravestone.

Of course, Croatians transcribed Croatian Serb names according to Croatian orthography, so for a Croatian Serb namesake the name would have been written as "Mileva Maric'", and no doubt, Croatians may have had the tendency writing her name "Maric'". However, note that she was not a Croatian Croat or a Croatian Serb, but a Hungarian Serb; the "Yugoslav" wars demonstrated the differences in the 90's.

After 1920 the new and artificial Yugoslav state accepted the "Illyrian theory" that Serbian and Croatian is one nation and one language, so Serbian obtained an official Latin orthography too (i.e. the Croatian), used now in the Voivodine and in Montenegro. So now a namesake of Mileva in her birthplace Titel should be written "Maric'". However in 1920. Mileva was already Mileva Einstein and was not interested in Illyrian theory anyways. Or you may assume Hungarian secret agents rewriting the Zurich gravestone against her last will. I return to the name in the Appendix.

If Magyars transcribe such names, they almost always use "cs" instead of "ty", which would be more phonetic. The "ty" must have come from Milos Marity Sr., reason unknown. Note that his son, brother of Mrs. Einstein, was student in physics at the Kolozsvár (Clausenburg, Cluj, Claudiopolis) University as Milos Marics. He remained for a while there as adjoint professor (Adjunkt) of department leader Apáthi.

#5 That is A. Einstein. But I note that the diplome work of M. Einstein, then Marity, was about thermodynamics. History of Science is unable to decide her part in the work, because in 1910 they lived together, so no written notes remained.

#6 In Hungary mandate is free. However if you defect your party group, you wait half a year as independent. Government parties, however, decided that the defectors were not defectors but a new party group. Remember this at #10. We have not heard anything on the deal up to now. (Maybe there was none at all.)

#7 Note that de Klerk told this after announcing the results of the election April 26-29, de Klerk transferred presidency to Mandela on May 9, and the speech was part of the process. Now, the first round of the Hungarian elections happened on May 8 and numbers were known to midnight with the result that Socialist absolute majority would almost be inevitable on May 29. So after one cycle old tendencies come back. This might have influenced de Klerk's prediction.

An interesting SA-Hungary parallel: at the very beginning of 1990 a high South African government delegation arrived at Hungary. The topics of the negotiations was not disclosed beforehand. After the negotiations on the press conference the South African delegation got the question: what was the topics? The answer: Why? Two fallen regimes discussed what to do.

#8 The split of Conservative MDF in Hungary and retirement of the leader of the Conservatives in South Africa and uncertainty in the party was cca. synchronous. I do not know why. This parallel was, it seems, never investigated.

#9 In Hungary a lot of conservative voters also went to liberal Fidesz in 1998. The shifts are comparable. In 1994 Green MDF got 12 % votes, Blue Fidesz 7, two other Greens 16 %. In 1998 MDF 3 % vs. Fidesz 28 % (and three other Greens 21 %).

#10 Now remember #6.

#11 E.g., it seems not trivial to integrate Afrikaans-speaking Calvinist Cape Coloureds into an English-dominated party. There is a Hungarian saying from the first half of 19th century: "The nation lives in her language." Of course, this is self-contradictory, because Hungarian language does not exist. The common language of old Hungary was Latin and the biggest Hungarian language is Magyar. Still the saying went against Germanisation and was successful. Now Afrikaans is considered an isolated language. While for a Magyar Afrikaans and English are almost dialects of each other (note that we are even not Indo-Europeans); a common language is a strong community-forming force.

Anthropologic differences between brown and white Afrikaans speakers are present. But also serious anthropological multiplicity appears within the Magyar-speaking population, albeit pigmented individuals are rarer there.

#12 Now again my Ural-Altaic identity surfaces. Trimurti seems to be trimorphic=of three forms. And because of this, for structure Trimurti is inherently tripolar. Here the word for "3" is the same in the Sanskrit, Greek and Latin terms, but it would also be the same in Russian, and even "three" is not too far. These languages do not really differ.

#13 Including language. He demonstrates that Vedic and Avestan are the same language, with dialectal differences, mainly in pronounciation. I am surprised why he tells that many Hindu and Parsee are surprised on this. For a Magyar speaker it is obvious that "asva" and "aspa" (horse) is the same word; "equus" is not too far either. Obviously Iranian visitors in India and vice versa did understand the speech. A Hungarian speaking one Slavic language generally can speak with other Slavs too, with some errors.

I tell here that Vedic "Veda" is "knowledge". Now Slovakian "knowledge" is also "Veda", so this is the name of the editorial house of the Slovak Academy of Sciences.

#14 Malicious Hungarian historians sometimes assume that the Hungarian Lenard overcompensated his Hungarian origin and wanted to be bigger or purer German than German Germans. To be clear, he was originally a Hungarian German (we call him Lénárd Fülöp, first name second as in Japanese) and the idea was that the was afraid to have some Magyar (so Asian) blood too. Maybe; maybe he became senile. His Nobel Prize earlier was for his real work about atomic structure.

#15 The space of phonemes cannot be a Riemannian space, because the number of phonemes is finite and restricted. The representations, the individual pronounciations are continuous; and they can be ordered according to the characteristics used in recognition. That is roughly the phonemes.

#16 Etymology cannot decide the question. Gothic is Eastern German and now such languages are extinct, but English "forbid" is "faurbiudan", where "-a-n" is the infinitive suffix; "au" is the low [o]. In Anglo-Saxon there was a diphtong in -beodan. On the other hand, Gothic "biugan" is "bend", it is "bugan" in Anglo-Saxon, with a long high monophtong. However in Icelandic there is a diphtong in bend=beygja. Here the "y" clearly indicate that the I-type sound of the diphtong comes from original U. (See e.g. Blakeley 1960; Glendening 1961; Holthausen 1934.) We do know that diphtongs evolved from long high vovels even in the last centuries of English, so this process may have happened in any time in German languages.

Abbot E. A. 1885: (under the pseudonym A Square) Flatland: A Romance in Many Dimensions.

Boston

Amara Lamea s.a.: http://home.online.no/~noetic/manda.htm

Anonymous s.a.: http://www.enemies.com/html/newtestament/IRAQ_yezidi.html

Anonymous 1997: wysiwyg://329/http://www.geocities.com/Athens/Parthenon/1170/greek.html

Anonymous 1999: http://www.cudenver.edu/stc~link/bkrvs/satclass/wors.htm

Anonymous 2000: Fundamentals of Vision, http://palaeo-electronica.org/2000_1/retinal/vision.htm

Anonymous 2001a: Here lies the National Party. Cape Business News, November

Anonymous 2001b: wysiwyg://107/http://www.wordonline.co.za/news/news_center_011031.411413.html

Aristotle, -60a: De Caelo. [You may use any editions; Bekker numbers are Bekker numbers.]

Aristotle, -60b: Meteorologica.

Armstrong Karen 1994: A History of God. A. A. Knopf, New York

Barbour J. B. & Bertotti B. 1977: Nuovo Cim. 38B, 1

Berkeley G. 1710: The Principles of Human Knowledge. Dublin

Bérczi Sz., Holba Ágnes & Lukács B. 1994: Evolution of Extraterrestrial Materials and Structures, Proc. 5th Symp. on Matter Evolution, eds. Lukács B. & al., KFKI-1994-22, p. 147

Bérczi Sz., Holba Ágnes, Lukács B. & Papp Éva 1996: in Side Tracks in Evolution. Proc. 7th Matter Evolution Symp., eds. Lukács B. & Bérczi Sz., KFKI-1996-07, p. 20

Blakeley L. 1964. Old English. Teach Yourself Books. The English Universities Press, London.

Borbély I. & Lukács B. 1989: Acustica 68, 52

Bowen J. T. & Rhys Jones T. J. 1960: Welsh. Teach Yourself Books. The English Universities Press, London

Brugmann K. 1904: Kurze vergleichende Grammatik der indogermanischen Sprachen. Trübner, Strassburg

Calland R. 2001: Daily Mail & Guardian Oct. 26

Chodos A. 1984: Comm. Nucl. Part. Phys. 13, 171

Chodos A. & Detweiler S. 1980: Phys. Rev. D21, 2167

Clarke A. C. 1956: Technical Error. In: Reach for Tomorrow. Ballantine Books, New York

Collinder (B. 1965: Acta Univ. Uppsal. Acta Soc. Ling. Uppsal. Nova Ser. 1, 109

Cull P. 2001: http://www.dispatch.co.za/2001/10/15/editorial/LP2.HTM

Dadrawala N. H. s.a.: http://members.ozemail.com.au/~zarathus/deen33f.html

Diósi L., Forgács B. Lukács B., & Frisch H. L. 1984: Phys. Rev. A29, 3343

Diósi L. & Lukács B. 1985: Phys. Rev. A31, 3415

Diósi L., Lukács B. & Rácz A. 1989: J. Chem. Phys. 91, 3061

Einstein A. 1905: Annln. Phys. 17, 891 (1905)

Einstein A. 1910: Annln. Phys. 33, 1275

Einstein A. 1916: Annln. Phys. 49, 898

Einstein A. 1933: in Mein Weltbild, p. 134

Einstein A: 1949: in Albert Einstein Philosopher-Scientist. Evanston, p. 1

Fehér P. & Hajdú Mária s.a. http://www.mek.iif.hu/porta/szint/tarsad/tudtan/grossmam.grossman.html

Ginneken van J. 1939: La Reconstriction Typologique des Langues Archaiques de l'Humanité, Amsterdam, Noord-Hollandsche Uitgevers-Maatschappi

Glasenapp H. von 1972: Die fünf Weltreligionen. Eugen Diederichs Verlag, Düsseldorf

Harms R. T. 1974: The Uralic Languages. Encyclopedia Britannica

Holba Ágnes & Lukács B. 1994: Élet és Tudomány 1994/26

Holba Ágnes & Lukács B. 1995: in Triality in Evolution, Proc. Sixth Workshop of Matter Evolution, eds. Lukács B. & al., KFKI-1995-21, p. 60

Holthausen F. 1934: Gothisches etymologisches Wörterbuch, Heidelberg.

Illy J. 1989: Ann. of Sci. 46, 417

Itkonen E. 1946: Zur Frage nach der Entwicklung des Vocalismus der ersten Silbe in den finnisch-ugrischen Sprachen, insbesondere im Mordwinischen. Finnisch-ugrische Forschungen (Helsinki), Vol. 29

Jóhanesson A. 1967: The Third Stage in the Creation of Human Language. Reykjavík & Oxford

Kumar S & Hedges S. B. 1998: Nature 392, 917

Lieberman Ph. & Crelin E. S. 1984: Linguistic Inquiry 11, 203

Lindeman F. 1981: Introduction to the Laryngeal Theory, Oxford

Lotz J. 1975: in Research in Altaic Studies, ed. Ligeti L., Budapest

Lukács B. 1988: Acta Phys. Pol. B19, 243

Lukács B. 1993: Magyar Szemle II, 866

Lukács B. 1994: Magyar Szemle III, 914

Lukács B., 1995a: In: Trialities in Evolution. Proc. 6th Symp. of the Evolution of Matter... eds. Lukács B. & al., KFKI-1995-21, p. 2

Lukács B. 2001: http://www.rmki.kfki.hu/~lukacs/lapedo.html

Lukács B. 2002: May Kaluza Ride Again? in Proc. Sixth Hungarian Relativity Workshop, ed. Hohenselaers C. & Perjés Z., Akadémiai Kiadó, Budapest

Lukács B. & Ladik J. 1993: Phys. Ess. 6, 39

Lukács B. & Pacher T. 1985: Phys. Lett. 113A, 200

Mach E. 1883: Die Mechanik in ihrer Entwicklung historisch-Kritisch dargestellt. Wien

Marais P. 2001: http://www.natweb.co.za/facts/fact12.htm

Martinás K. & Lukács B.: KFKI-1984-77

Marsina R. 1997: Human Affairs 7, 15

Matshikiza J. 1999: Daily Mail & Guardian, May 27

Mayrhofer M. 1986: Lautlehre: segmentale Phonologie der Indogermanischen. 2. Halbband, Band I, Indogermanische Grammatik. Heidelberg, Carl Winter

Mehta A. 2001: Zarathushtra. http://homepage.mac.com/ardeshir/Zarathushtra-Ch.1-6,Draft.pdf

Melchizedek D., 1998: The Ancient Secret of the Flower of Life. Light Technology Publ., Sedona

Mollon J. 1992: Nature 356, 378

Moulton W. G. 1948: Language 24, 81

Newton I. 1704: Opticks: or a Treatise of the Reflections, Refractions Infextions and Colours of Light. London

Névmutató s.a. www.omgk.hu/MGGEPGY/nevm.html

O’Connor J. T. 1984: The Father’s Son. Daughters of St. Paul, Boston

Pacher T. 1985: Theses. ELTE, Budapest

Palacios A. G., Martinoya C., Bloch S. & Varela F. 1990: Vision Res. 30, 587

Palmer G. 1777: Theory of Colours and Vision. Leacroft, London

Peterson G. E. & Barney H. L. 1952: J. Acoust. Soc. Amer. 24, 175

Planck M. 1900: Lecture at the German Physical Society, Berlin, 14th Dec.

Renn J. & Schulmann R. 1992: Albert Einstein - Mileva Maric'; The Love Letters. Princeton University Press, Princeton

Rostron B. 2000: New Statesman Dec. 18

Ruppeiner G. 1983: Phys. Rev. Lett. 50, 287

Sapa 2001a: wysiwyg://170/http://iafrica.com/news/sa/850757.htm

Sebestyén Á. 1980: KFKI-80-133

Seidler G. L. 1964: Mysl politiczna sredniowiecza. Wydawnictwo Literackie, Krakow

Skello S. 2001: wysiwyg://154/http://www.news24.co.za/City_Press/City_Press_Leaders/0,1885,186-189_1116025,00.html

Steinitz W. 1944: Geschichte des finnisch-ugrischen Vocalismus, Stockholm

Toynbee A. 1979: A Study of History. Weatherwane, New York

Trbuhovic'-Gjuric' Desanka 1969: U senci Alberta Ajnstajna, Bagdala, Krushevac

Varela F. J., Palacios A. G. & Goldsmith T. H. 1993: in Vision, Brain and Behavior in Birds, eds. Zeigler & Bishof, MIT Press, Cambridge Mass.

Vizgin V. P., 1981: Relyativistskaya teoriya tyagoteniya (istoki i formulirovanie 1900-1915), Nauka, Moscow

Wasserman G. S. 1978: Color Vision, J. Wiley & Sons, New York

Weinberg J. 1976: Gen. Rel. Grav. 7, 135

Wells, H. G. s.a.: The Plattner Case

Young T. 1802: Phil. Transact. Rey. Soc. London, 92, 20

Zorpette G. 2000: Red Herring Magazine, Nov. 1

My HomePage, with some other studies, if you are curious.