QUARK GLUON PLASMA
Seltsame Quark Produktion
Die Produktionsrate von seltsamen Quarks und Antiquarks
in einem thermalisierten Quark Gluon Plasma wurde
als Bestandteil meiner Doktorarbeit unter der Betreuung
von J. Zimányi gerechnet.
Diese perturbative Rechnung in der führenden Ordnung
der QCD hat es gezeigt, dass die Equilibrierungszeit
bei der Produktion von seltsamen Quarks in der
Grössenordnung von einige fm/c liegt und durch
den Prozess gg -> ss dominiert ist
[5,
8,
13,
14] .
Diese Arbeit wurde gleichzeitig mit der ähnlichen
Arbeit von B. Müller und J.Rafelski
gefertigt.
In 1990 kehrte ich zum diesen Problem zurück
bei der Berechnung der Produktionsrate von seltsamen
Quarks in einem Plasma, welches massive Gluonen
beinhaltet. Meine Mitarbeiter waren diesmal
P.Lévai und B.Müller .
Wenn Gluonen genügend Masse besitzen würden,
würde der Gluonzerfallprozess g -> ss auch
beitragen [32] .
Laut spätere perturbative Rechnungen stellte sich
aber heraus, dass die Quarks so massiv werden
im QGP, dass der obige Zerfall nicht stattfinden kann.
Gluonmasse
Die Gluonmasse, als der statische, langwellige Grenzfall
der gluonischen Selbstenergie ist für die Wechselwirkung
im Quark Gluon Plasma charakteristisch. Deshalb kann sie
für die Parametrisierung nichtidealen
Zustandsgleichungen benutzt werden.
Die Gluonmasse kann auch als Ordnungsparameter in der
Variationsnäherung zur QCD benutzt werden, wobei
sie eine Phasenübergang erster Ordnung bezeichnet.
In den Jahren 1987 - 1989 arbeitete ich an einem solchen
Variationsmodell der QCD mit dem Ergebnis, dass die
wichtigste phenomenologische Aspekte, vom Gluonkondensat
bis die Einschließung von schweren Quarks, mit diesem
einzelnen Parameter, der Gluonmasse, beschrieben werden
konnten
[5,
25,
27,
29,
31,
35].
Diese Untersuchungen sind auch in meiner Habilitationsschrift
vorgeführt.
Weitere Arbeiten, die sich mit der Problematik des
Confinements beschäftigen, können in
[23,
28]
gefunden werden.
Abschirmung
In einem Gluonplasma die thermische Abschirmungsmasse,
welche das Coulomb-Potential zwischen zwei schweren Ladungen
zum Yukawa-Potential modifiziert, kann relativ einfach
berechnet werden; analog zur Berechnung der Debye-Masse
in einem Plasma von elektrischen Ladungen.
Gemeinsam mit Dr. B. Müller und Dr.
X. N. Wang gefertigten wir eine Abschätzung
der Debye-Masse im anisotropen Partonmedium, wobei der
Polarisationstensor nicht mehr spherisch ist.
Ein gewisser Unterschied zwischen longitudinalen
(in der Richtung paralell zur Bewegung der Testladung)
und transversalen (orthogonal zur obigen Richtung)
Debye-Massen wurde gefunden
[36] .
Magnetische Abschirmung
Die statische, langwellige magnetische Abschirmung kann nicht wie die
Debye-Masse perturbativ berechnet werden.
Mit Dr. B. Müller machten wir eine Abschätzung
dieser Größe durch Stabilisierung von semiklassichen
Soltionslösungen der Yang-Mills-Gleichungen, die
eine magnetische Monopolladung für den entfernten
Beobachter vortäuschten. Diese Lösungen konnten
nach Einführung eines skaleninvarianzbrechendes
Energiegliedes gefunden werden.
Die Dichte solcher Konfigurationen wurde dann in der
Sattelpunkt-Näherung gerechnet und schließlich
eine Integration des künstlichen Skalenparameters
ergänzte die Rechnung.
Wir haben eine magnetische Masse von
m = 0.255 g ² T
für die Gruppe SU(2) [37]
erhalten.
Chaos
Meine Forschungen über die chaotische Dynamik
der klassischen Hamiltonschen Gittereichtheorie
fingen in 1991 an, wann gemeinsam mit
B.Müller, A.Trayanov and C.Gong
an der Duke University durchführten wir
eine Reihe von Berechnungen für SU(2), U(1)
und SU(3) Systeme.
Es wurde die Skalierung des führenden Lyapunov-Exponents
mit der totalen Energie der anfänglichen
Feldkonfiguration und das gesamte Lyapunov-Spektrum
von kleinen Gitter bestimmt
[6,
40].
Eine Übersicht der Rolle des Chaos in der
Eichfeldtheorie kann in unserem Buch
[7]
(Koauthoren S. Matinyan and B. Müller )
gefunden werden.
Spätere Entwicklungen sind in
[43,
44,
45]
veröffentlicht.
Untersuchungen zum Effekten von statischer Ladungen
[46]
und Higgs-Felder
[47]
folgten.
Gegenwärtig studieren wir die Lyapunov Exponenten
von Gittereichkonfigurationen, die in quantum Monte Carlo
Simulationen erzeugt wurden (Mitarbeiter H. Markum ).
Ein Beispielkonfiguration auf dem Gitter
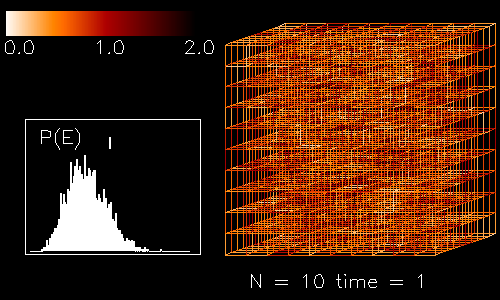
Ein Beispielkonfiguration auf einem 10x10x10 Gitter
ist gezeichnet. Die Energie zu jedem Link
wurde als Durchschnitt von den 1-Tr(Up) Werten
auf den anliegenden Plaquetten berechnet.
Auf dem Bild diese Energie ist kodiert
durch die Farbe im Intervall von (0,2).
Der Diagramm zeigt die Verteilung der Energie
bei eindlicher Temperatur in der Deconfinement-Phase.
