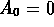 mértékrögzítés
melletti tanulmányozásával demonstrálható.
mértékrögzítés
melletti tanulmányozásával demonstrálható.
Kutatási tervünk lényegét a forró gluon plazma tanulmányozásában mostanában felmerült ellentmondások ismertetésével szeretnénk felvázolni. Az ezen ellentmondás feloldására irányuló kutatás azonban más fizikai rendszerekre is ki fog terjedni.
A hosszúhullámú, klasszikus, nemábeli Yang-Mills mezok
kaotikus dinamikája legjobban a gluonikus zéró módusok
Hamilton függvnyének az 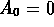 mértékrögzítés
melletti tanulmányozásával demonstrálható.
mértékrögzítés
melletti tanulmányozásával demonstrálható.
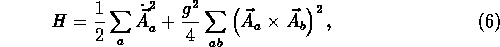
a térbeli deriváltak elhanyagolásával.
Feltétel;ezve, hogy csak két vektorpotenciál komponens,
pl.
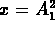 and
and 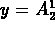 (vagyis egy színben és polarizációban
duális pár) különböznek nullától,
a Hamilton függvény redukálható:
(vagyis egy színben és polarizációban
duális pár) különböznek nullától,
a Hamilton függvény redukálható:
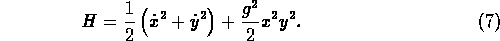
Ez egy pontszeru részecske konzervatív mozgását
írja le két dimenzióban. A potenciális energia,
amely 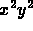 -tel arányos, egy hiperbolát definiál, mint
az adott energiájú klasszikus mozgás határát.
Ez a határ egyben a klasszikus trajektóriák fordulópontjait
is jelenti. Amíg a tengelyek közelében (
-tel arányos, egy hiperbolát definiál, mint
az adott energiájú klasszikus mozgás határát.
Ez a határ egyben a klasszikus trajektóriák fordulópontjait
is jelenti. Amíg a tengelyek közelében ( vagy
vagy
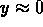 ) a mozgás kvázi-reguláris, addig a klasszikusan
megengedett tartomány nagy részében kaotikus.
A hiperbolikus határfelület egy tükrözo falként is
felfogható, amely a közeli párhuzamosan beeso
trajektóriákat defókuszálja a negatív görbülete
miatt [3-5].
) a mozgás kvázi-reguláris, addig a klasszikusan
megengedett tartomány nagy részében kaotikus.
A hiperbolikus határfelület egy tükrözo falként is
felfogható, amely a közeli párhuzamosan beeso
trajektóriákat defókuszálja a negatív görbülete
miatt [3-5].
Véges homérsékleten fellépo közegeffektusok, mint pl. a plazmabeli Debye árnyékolás, e hosszúhullámú mezoknek tömeget generál [31, 32]. A Hamilton függvény módosul e kvantumeffektus hatására:
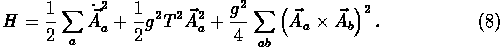
A dinamikus tömeg, gT, arányos a T homérséklettel. Ez a rendszer csak akkor viselkedik kaotikusan, ha az
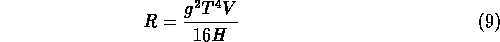
kontrollparaméter értéke a kritikus 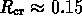 alá esik.
Egy szabad gluonokból álló sugárzási gáz energiasurusége
magas homérsékleten
alá esik.
Egy szabad gluonokból álló sugárzási gáz energiasurusége
magas homérsékleten 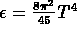 a
Stefan -- Boltzmann sugárzási törvény értelmében.
Feltéve, hogy azonos mennyiségu energia, azaz
a
Stefan -- Boltzmann sugárzási törvény értelmében.
Feltéve, hogy azonos mennyiségu energia, azaz
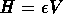 koncentrálódik a kaotikusan viselkedo
infravörös x és y módusban, azt várjuk, hogy a káosz
az
koncentrálódik a kaotikusan viselkedo
infravörös x és y módusban, azt várjuk, hogy a káosz
az
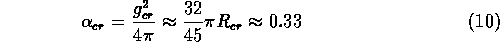
-nál gyengébb csatolási állandó mellett fejlodik ki.
Ez az érték a színfelszabadítás
(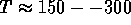 MeV)
tartományába esik. Ilyen magas homérsékletek
eléréséhez elegendo energia a CERN SPS és a RHIC
nehézion kisérleteiben elérhetok.
MeV)
tartományába esik. Ilyen magas homérsékletek
eléréséhez elegendo energia a CERN SPS és a RHIC
nehézion kisérleteiben elérhetok.
Ez a várakozás ellentétben áll a forró perturbatív
QCD megközelítésével, ahol az 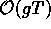 nagyságú
tömegtag alacsonyabb rendben adódik, mint a kaotikus dinamikával
kapcsolatos mennyiségek, pl. a gluon csillapítási
tényezo, ami
nagyságú
tömegtag alacsonyabb rendben adódik, mint a kaotikus dinamikával
kapcsolatos mennyiségek, pl. a gluon csillapítási
tényezo, ami 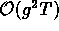 nagyságrendu.
A puha plazmonok, vagyis a hosszúhullámú, alacsony energiájú
térkomponensek effektív Hamilton függvényét itt
a
nagyságrendu.
A puha plazmonok, vagyis a hosszúhullámú, alacsony energiájú
térkomponensek effektív Hamilton függvényét itt
a  -tel arányos sajátenergia tag uralja.
Ebben a megközelítésben kis x és y amplitúdókra
nem fedezheto fel kaotikus viselkedés [33].
-tel arányos sajátenergia tag uralja.
Ebben a megközelítésben kis x és y amplitúdókra
nem fedezheto fel kaotikus viselkedés [33].
Azért, hogy e két szembenálló nézet között közvetíthessünk és nem-egyensúlyi helyzetekben is realisztikus leírását adhassuk a gluondinamikának, javasoljuk a klasszikus és kvantumeffektusok relatív szerepének a kutatását kiterjedt elemi mezorendszerek kaotikus vagy nem kaotikus természetében.