

Next: Kapcsolódó kutatások
Up: No Title
Previous: References
A káoszt sokan kutatják. Javaslatunkban egy különleges
anyag, a relativisztikus kvantumterek kaotikus viselkedését
tanulmányoznánk. E terek közül is leginkább a
mértéktereket, amelyek az elemi részecskék kölcsönhatásait
írják le a modern fizikában.
Bár a mértékelv már Yang és Mills [1] 1954-ben
bevezetett nemábeli mértékelméletében is jelen volt,
ezen elméletek, mint a fizikai kölcsönhatások elemi leírásai,
csak az 1970-es években kezdték diadalútjukat [2].
A mértékterek kaotikus viselkedését az 1980-as években
kezdték tanulmányozni analitikusan megoldható nemlineáris
egyenletek segítségével. Az ún. Yang-Mills és
Yang-Mills-Higgs mechanika a térleméletet néhány szabadsági
fokra egyszerusítette, amelyek kaotikus viselkedését
analitikus és numerikus módszerekkel egyaránt tanulmányozták
[3,4,5].
Az idofüggo, gömbszimmetrikus megoldás, a Wu-Yang
monopólus [6] instabilnak bizonyult a Fermi-Pasta-Ulam módszer
alkalmazásával [7-10].
Általánosságban a dinamikusan képzett tömegek káoszt
csökkento hatása nyert bizonyítást [4].
A térelméleti numerikus módszerek fejlodése, különösen
a rács -- térelmélet [11-13] nagyobb rendszerek számítógépes
tanulmányázását is lehetové tette.
Modern lehetoségek 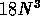 (N=30-ig) szabadsági fokú rendszerek
számítógépes szimulációját hozták magukkal az
1990-es években.
A hamiltoni rács -- mértéklemélet formalizmusával klasszikus,
valós ideju dinamikai szimulációk történtek
U(1), SU(2) és SU(3) szimmetria esetére [14-17].
E kutatásokban a Lyapunov hatványok teljes spektrumát,
ami az entrópia növekedésével kapcsolatos, kiszámolták.
A nemábeli plazmahullámok instabilitását is ilyen számítógépes
munkák demonstrálták [18].
(N=30-ig) szabadsági fokú rendszerek
számítógépes szimulációját hozták magukkal az
1990-es években.
A hamiltoni rács -- mértéklemélet formalizmusával klasszikus,
valós ideju dinamikai szimulációk történtek
U(1), SU(2) és SU(3) szimmetria esetére [14-17].
E kutatásokban a Lyapunov hatványok teljes spektrumát,
ami az entrópia növekedésével kapcsolatos, kiszámolták.
A nemábeli plazmahullámok instabilitását is ilyen számítógépes
munkák demonstrálták [18].
A klasszikus közelítés érvényességét 1993-ban
Gauss -- hullámcsomagok tanulmányozásával vizsgálták [19].
A vezeto Lyapunov kitevo és a forró perturbatív
QCD-ben számolt gluon csillapítási
tényezo számszerU egybeesését
mostanában (1995) sikerült megmagyarázni [20].
Mindeme kutatások a nagy energiasuruségek fizikájának
megértését célozták, amelyek gyorsítós
kisérletekben és a korai Univerzumban fordulhattak elo.
Léteznek azonban olyan meggondolások is, amelyek szerint
az elemi terek kaotikus dinamikája a fizikai vákum tulajdonságaiban
is szerepet játszik [21, 22]. Egy híres példa a kvarkok
és gluonok, valamint egyéb színtöltések bezárása.
A térelméleti káosz tanulmányozása most érkezett el ahhoz
a ponthoz, amikor a klasszikus és kvantumfizika összefüggéseit,
valamint a rövid- (inkább kvantumos) és hosszúhullámú
(inkább klasszikus) mezokomponensek kölcsönhatásait
magas homérsékleten elkezdhetjük tanulmányozni.


Next: Kapcsolódó kutatások
Up: No Title
Previous: References
Biro Tamas 17-98
Thu Aug 3 14:30:23 CDT 1995
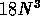 (N=30-ig) szabadsági fokú rendszerek
számítógépes szimulációját hozták magukkal az
1990-es években.
A hamiltoni rács -- mértéklemélet formalizmusával klasszikus,
valós ideju dinamikai szimulációk történtek
U(1), SU(2) és SU(3) szimmetria esetére [14-17].
E kutatásokban a Lyapunov hatványok teljes spektrumát,
ami az entrópia növekedésével kapcsolatos, kiszámolták.
A nemábeli plazmahullámok instabilitását is ilyen számítógépes
munkák demonstrálták [18].
(N=30-ig) szabadsági fokú rendszerek
számítógépes szimulációját hozták magukkal az
1990-es években.
A hamiltoni rács -- mértéklemélet formalizmusával klasszikus,
valós ideju dinamikai szimulációk történtek
U(1), SU(2) és SU(3) szimmetria esetére [14-17].
E kutatásokban a Lyapunov hatványok teljes spektrumát,
ami az entrópia növekedésével kapcsolatos, kiszámolták.
A nemábeli plazmahullámok instabilitását is ilyen számítógépes
munkák demonstrálták [18].