![]()
THE GEOMETRY OF LIE GROUPS |
Lie groups like SU(N) display a nontrivial curved geometry in the angular variable space. The geometrical properties of the group space define a local metric tensor and through that covariant operations and invariant quantities like the scalar curvature and the Laplace operator. These can be used for derive formulae for group integrals or Casimir operators and hence lattice Hamiltonians more generally. In this section we take a brief excursion to this field exploring some basic ideas and presenting various useful results.
The basis of any geometrical description is a measure of distances, surfaces and volumes which is locally governed by the metric. In order to measure distances between two elements of a group we need to know the length of their displacement vector, which requires the definition of a norm. In fact a real valued scalar product can be defined in a natural way in the matrix representation
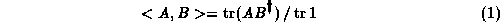
for SU(N) or more generally for any Lie group. This scalar product has the desired properties
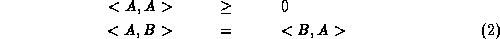
The elements U of the SU(N) group are vectors of unit length, so
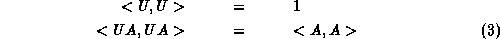
for any matrix A (not necessarily a group element). The invariant infinitesimal distance square
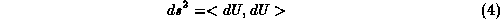
defines the components of the metric tensor 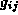 in a given representation
in a given representation
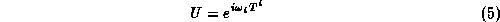
through
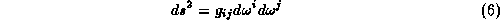
where 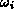 are the group parameters (in SU(N) compact angular variables)
and the
are the group parameters (in SU(N) compact angular variables)
and the 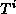 are the basis matrices for a given representation. They satisfy
the commutation relation
are the basis matrices for a given representation. They satisfy
the commutation relation
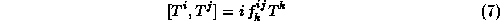
with the totally antisymmetric structure constants 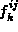 of the
associated Lie algebra.
of the
associated Lie algebra.
Now one point here is still to clarify: how do we differentiate a group
element U?
A possibility would be to follow the general definition and take the
limit of the difference of two neighboring elements. To define
a neighborhood, however, we need a parameterized form, therefore
we would obtain a parametric derivative.
Another possibility is to construct first a one-form, a combination of
the coordinate differentials 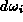 without making reference to
a special parameter set, and then consider the length of this differential.
More generally we consider the following action on a matrix X
without making reference to
a special parameter set, and then consider the length of this differential.
More generally we consider the following action on a matrix X
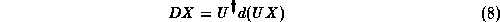
as the covariant differential. Expanding this leads to the abstract operator equality
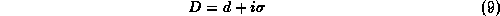
with
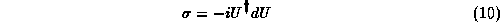
being the parallel transport or connection form. It may be familiar
to the reader from Riemannian geometry or from the theory of general
relativity.
In fact there is a striking analogy between the gauge covariant and
geometrically covariant derivatives.
In the theory of Lie groups  is called the Mauer-Cartan one-form.
Since its square length
is called the Mauer-Cartan one-form.
Since its square length
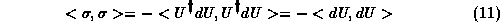
equals the infinitesimal distance squared (apart from the sign) it is sometimes also called the half-metric of the group. Since the vectors U have unit length it is easy to see that the Mauer-Cartan form defined above is hermitean
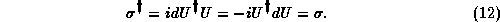
The following useful identity
where the index ``ad'' refers to the adjoint representation, which uses
the Lie algebra structure constants as basis 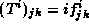 and therefore
and therefore
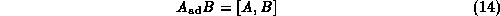
for any matrix B,
can be used for the evaluation of the covariant derivative.
Note that the adjoint representation of 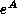 is
equivalent with an infinite series of using n-fold commutators
is
equivalent with an infinite series of using n-fold commutators
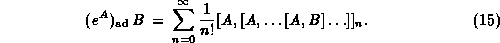
| Exercise: | Prove the identity (13). |
| Solution: | First we define
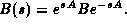 Realizing that Realizing that
we use the Taylor expansion
to obtain
|
Now using the power series form of (13) and applying it for the differential operator B=d we realize that, since
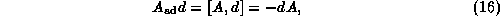
the covariant derivative is
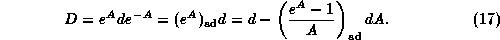
Replacing now 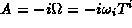 in this result we obtain the
Mauer-Cartan form
in this result we obtain the
Mauer-Cartan form
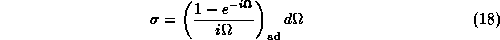
Writing this in component form
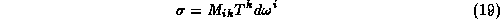
we obtain the components of the metric tensor
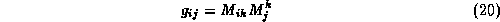
where a summation over the index k is understood. The normalization of the basis matrices
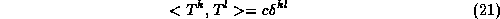
is representation dependent. If the group elements were represented in
the fundamental representation of SU(N) the normalization is 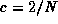 ,
in the adjoint representation it is
,
in the adjoint representation it is 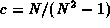 .
Once the metric tensor in a given representation is known, the group
integral can be carried out by using the Jacobian
.
Once the metric tensor in a given representation is known, the group
integral can be carried out by using the Jacobian  which leads to the Haar measure
which leads to the Haar measure
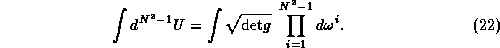
![]()
Let us demonstrate the above in the case of SU(2). In the fundamental
representation the matrix 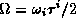 has the eigenvalues
has the eigenvalues
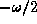 and
and 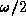 where
where  is the
length of the vector
is the
length of the vector 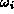 . Correspondingly the projectors
. Correspondingly the projectors 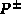 onto the eigenstates with eigenvalue
onto the eigenstates with eigenvalue 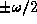 satisfy
satisfy
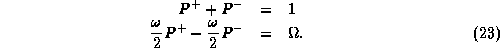
Introducing the matrix 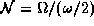 the projectors are
the projectors are
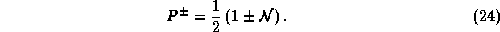
Using the eigenvalues and projectors any function of the matrix 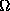 can easily be obtained, especially
can easily be obtained, especially
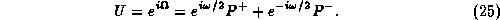
It can be rearranged into the familiar form
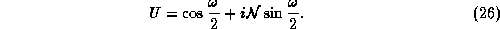
In order to obtain the Mauer-Cartan form and the metric tensor we need
the adjoint representation as well. In this case we consider a spin 1
system and the eigenvalues of 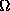 are
are 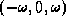 .
The corresponding projectors satisfy
.
The corresponding projectors satisfy
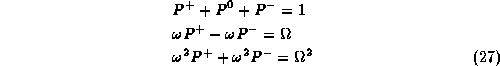
leading to
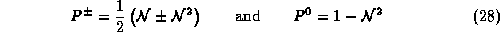
with 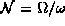 this time.
The Mauer-Cartan form becomes
this time.
The Mauer-Cartan form becomes
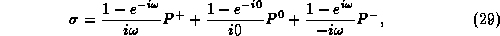
which can be written in the form
with
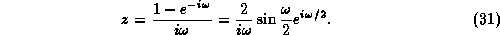
In order to have 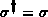 the projectors must satisfy
the projectors must satisfy
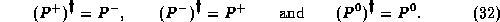
As a consequence two projectors have zero length
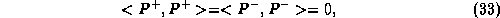
while from the trace relations 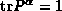 for any
for any
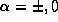 we get
we get
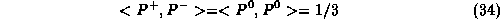
in the adjoint SU(2) representation. This finally leads to
| Exercise: | Calculate the determinant of the matrix
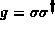 . . |
| Solution: | The determinant of a matrix is the product
of its eigenvalues. Since we
have according to (30)
we obtain
|
Finally using the radial coordinates
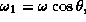
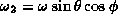 and
and
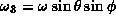 we obtain the following invariant infinitesimal distance
we obtain the following invariant infinitesimal distance
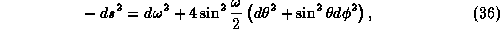
and the following integration measure
These results show that the geometry of the group SU(2) is analogous to that
of a surface of the four dimensional sphere with unit radius  .
The essential difference is global: SU(2) can be wrapped twice over
.
The essential difference is global: SU(2) can be wrapped twice over
 , which is obvious since here
, which is obvious since here 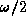 is the main asimuthal angle.
It is also obvious that the curvature of this space is constant.
is the main asimuthal angle.
It is also obvious that the curvature of this space is constant.
![]()
The Laplace operator in this space, corresponding to the electric energy in the
quantized Hamiltonian lattice gauge theory, can be
written according to the above metric as
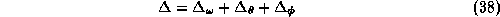
with second derivatives according to spherical angular coordinates in four dimensions
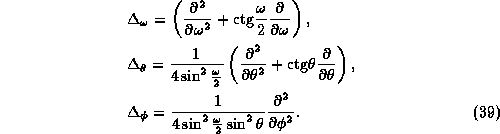
The solutions of the free SU(2) Schrödinger equation,
include the spherical functions
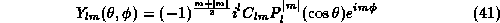
with the coefficients 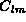 being
being
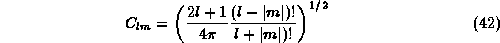
and the associated Legendre polynomials 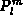 satisfying
satisfying
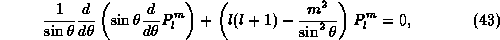
such that the radial dependence 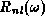 factorizes
factorizes
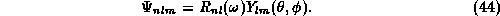
The 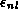 eigenvalues in this case correspond to the pure electric
energy density of a flux line spanned over a lattice link.
eigenvalues in this case correspond to the pure electric
energy density of a flux line spanned over a lattice link.
In comparison with the familiar spherical functions known from the Schrödinger equation for radially symmetric potentials in three-dimensional space the radial part of the eigenfunctions of the SU(2) Schrödinger equation (40) is somewhat unusual. It satisfies the eigenvalue equation
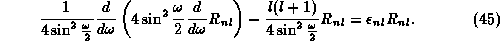
The ansatz
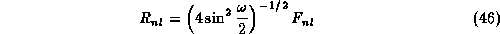
separates some trivial factors leading to
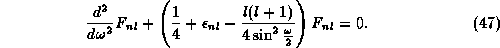
This equation defines the ultraspherical functions
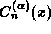 so that two classes of solutions occur
so that two classes of solutions occur
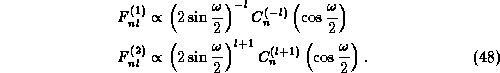
The proportionality factors are obtained from the normalization
of the wave function.
Finally, the solution, which is regular at 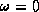 , is given by
, is given by
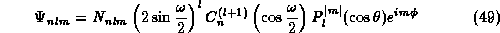
with the normalization coefficient
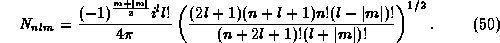
The energy eigenvalues are those of a quantized rotator
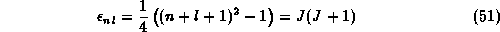
with 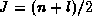 being an integer or a half integer.
being an integer or a half integer.
Finally, it is interesting to note that the radial excitations of the SU(2) quantum rotator constitute the character function of the group in the representation J
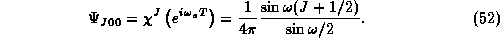
Writing this result in the alternate form
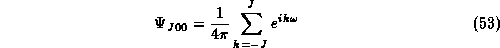
one easily realizes that J=0 belongs to the vacuum, 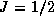 to the
fundamental and J=1 to the adjoint representation of the SU(2) group.
For gauge fields on lattice links the lowest excitation corresponds to
J=1.
to the
fundamental and J=1 to the adjoint representation of the SU(2) group.
For gauge fields on lattice links the lowest excitation corresponds to
J=1.
At finite temperatures on the other hand, every excitation is allowed. Since the degeneracy of a multiplet J is
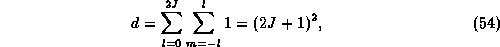
the partition function for the electric field energy eigenvalues
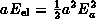
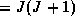 on a link of
length a can be obtained as
on a link of
length a can be obtained as
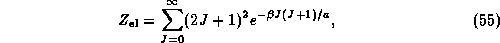
with 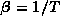 being the inverse temperature.
In the gluon sector we sum over integer values of J only.
The average electric energy can be obtained as
being the inverse temperature.
In the gluon sector we sum over integer values of J only.
The average electric energy can be obtained as
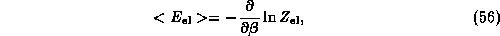
and the effective number of degrees of freedom
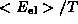 can be inspected as a function of temperature.
can be inspected as a function of temperature.
As expected, at high temperatures the average electric energy approaches
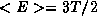 . Assuming equipartition at high temperature this yields
<E>=3T including the magnetic energy. Corresponding to an ideal
gas of massless relativistic SU(2) gluons. At low temperature,
however, even if all links were independent, i.e. the interlink coupling
through the magnetic energy were neglected, the electric gauge degrees of freedom
would be frozen. This situation is analogous to the Dulong-Petit rule,
known from solid state physics.
. Assuming equipartition at high temperature this yields
<E>=3T including the magnetic energy. Corresponding to an ideal
gas of massless relativistic SU(2) gluons. At low temperature,
however, even if all links were independent, i.e. the interlink coupling
through the magnetic energy were neglected, the electric gauge degrees of freedom
would be frozen. This situation is analogous to the Dulong-Petit rule,
known from solid state physics.