QUARK GLUON PLASMA

Strange Quark Production

The production rate of strange quarks and antiquarks in a thermalized quark gluon plasma was calculated during my PhD thesis supervised by J. Zimányi . This leading order calculation in the perturbative QCD showed that the equilibration time of strange quark production is in the order of a few fm/c and is dominated by the gg -> ss process [5, 8, 13, 14] . This work has been done contemporarily with a similar work of B. Müller and J.Rafelski .

In 1990 I returned to this problem again by calculating the strange quark production rate in a plasma of massive gluons with Drs P.Lévai and B.Müller . If gluons were more massive then two strange quarks also the g -> ss one gluon decay would contribute [32] . According to recent perturbative estimates, however, this is not the case, so in general the in-medium production rates are somewhat reduced.

Gluon Mass

The gluon mass, obtained from the static, long-wavelength limit of the gluon self-energy characterizes the degree of interaction in a gluon plasma. It can therefore be used for parametrizing the non-ideal equation of state.

Furthermore, in the framework of variational approach to the QCD at low and high temperatures the gluon mass can be used as an order parameter signalling a first order phase transition of the pure glue. In the years 1987 - 1989 I worked out such a variational model of QCD which describes the most important phenomenological aspects from the gluon condensate to heavy quark confinement using a single scale parameter, the gluon mass, only [5, 25, 27, 29, 31, 35].

These investigations are also reviewed in my habilitation thesis. Further work related to the confinement phenomenology can be found in [23, 28].

Screening

In a gluon plasma a thermal screening mass, which modifies the Coulomb potential between heavy charges to a Yukawa type one, can be calculated relatively easily in analogy to the calculation of the Debye mass in a plasma of electric charges.

With Drs B. Müller and X. N. Wang we estimated the Debye mass in an anisotrop parton medium; the polarisation tensor looses its sphericity in this case. A slight difference between longitudinal (paralell moving test charge) and transverse (orthogonally moving test charge) Debye masses has been found [36] .

Magnetic Screening

Unlike the Debye mass a static, long wavelength magnetic screening cannot be described perturbatively. With B. Müller we estimated this quantity by stabilizing solitons carrying a magnetic monopole charge in a semiclassical calculation due to a scale invariance breaking energy term. The density of such configurations was then obtained in a saddle point approximation and finally an integration over the artificially induced scale completed the calculation. We obtained a static magnetic mass of

m = 0.255 g ² T

for SU(2) [37] .

Chaos

My investigations about the chaotic dynamics of the classical Hamiltonian lattice gauge theory started in 1991 when together with B.Müller, A.Trayanov and C.Gong at the Duke University we carried out a series of calculations for SU(2), U(1) and SU(3) systems. The scaling of the leading Lyapunov exponent with the total energy of the initial configuration and for small lattices the complete Lyapunov spectrum has been obtained [6, 40].

A review of the role of chaos in gauge theory can be found in our recently published book [7] (co-authors S. Matinyan and B. Müller ). Further developments are published in [43, 44, 45] .

Investigations of the effect of static charges [46] and Higgs fields [47] followed. Recently we study the Lyapunov exponent for lattice configurations generated by quantum Monte Carlo simulations (collaborator H. Markum ).

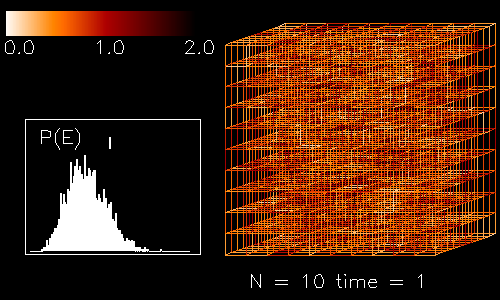
A sample configuration on the lattice

This figure shows a sample configuration on a 10 x 10 x 10 lattice. The 1-Tr(Up) values are averaged for all four plaquettes attached on a given link. These are color coded in the interval (0,2).

The diagram shows the distribution of the plaquette energies at a finite temperature.